历届高考数学真题汇编专题6_不等式最新模拟_理 24页

‎【备战2013年】历届高考数学真题汇编专题6 不等式最新模拟 理 ‎1、（2012滨州二模）不等式｜x－5｜－｜x－1｜＞0的解集为 ‎ （A）(－，3)　　　　　（B）(－，－3)　　 ‎ ‎（C）(3，＋)　　　　　（D）(－3，＋)‎ ‎2、（2012德州二模）已知函数则f（x）≤1的x的取值范围是 。‎ 答案：（－，－3］［－1，＋）‎ 解析：依题意，有｜x－1｜－｜2x＋3｜≤1，‎ ‎①当x≤－时，原不等式化为：1－x＋2x＋3≤1，解得：x≤－3，所以x≤－3；‎ ‎②当－＜x＜1时，原不等式化为：1－x－2x－3≤1，解得：x≥－1，所以－1≤x＜1；‎ ‎③当x≥1时，原不等式化为：x－1－2x－3≤1，解得：x≥－5，所以x≥1；‎ 综上可知：x的取值范围是（－，－3］［－1，＋）‎ ‎3、（2012德州一模）若直线平分圆，则的最小值是( )‎ ‎ A． B． C．2 D．5‎ ‎4、（2012济南3月模拟）已知实数x,y满足|2x+y+1|≤|x+2y+2|，且，则z=2x+y的最大值 A. 6 B. ‎5 C. 4 D. 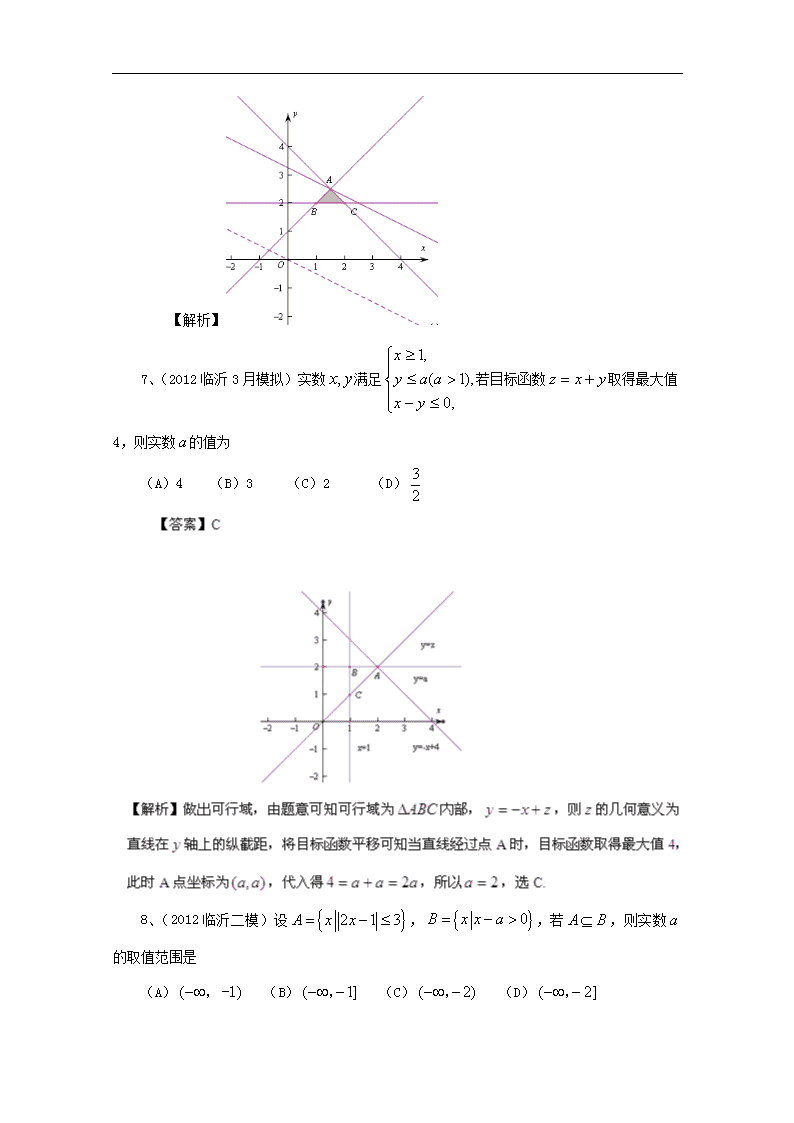-3‎ ‎【答案】B ‎5、（2012济南三模）若全集R，集合，｛｝，则 A． B．　C． D． ‎ 答案：D 解析：因为 ，‎ ‎，所以，所以，选D.‎ ‎6、（2012莱芜3月模拟）若设变量x，y满足约束条件，则目标函数的最大值为 ‎ ‎ (A)10 (B)‎12 ‎(C)13 (D) 14‎ ‎【答案】C ‎【解析】‎ ‎7、（2012临沂3月模拟）实数满足若目标函数取得最大值4，则实数的值为 ‎（A）4 （B）3 （C）2 （D）‎ ‎8、（2012临沂二模）设，，若，则实数的取值范围是 ‎（A） （B） （C） （D）‎ ‎【答案】A ‎【解析】集合，而，因为，所以，选A.‎ ‎9、（2012青岛二模）设变量满足约束条件：,则目标函数的最小值为 .‎ 答案：‎ ‎【解析】画出可行域得点为选用目标，所以 ‎10、（2012青岛3月模拟）已知,且,则的最小值为 A. B. C. D. ‎ 答案：C ‎【解析】‎ ‎11、（2012日照5月模拟）在约束条件下，当时，目标函数的最大值的变化范围是 .‎ ‎12、（2012泰安一模）函数＞，且的图象恒过定点A，若点A在直线上（其中m，n＞0），则的最小值等于 A.16 B‎.12 ‎ C.9 D. 8‎ ‎【答案】D ‎【解析】令，得，此时，所以图象过定点A,点A在直线,所以，即.，当且仅当，即时取等号，此时，选D.‎ ‎13、（2012烟台二模）已知函数若，且，都有不等式成立，则若实数x的取值范围是＿＿＿‎ 答案：［0,4］‎ 解析：因为｜a＋b｜＋｜a－b｜≥2｜a｜，依题意，得：‎ ‎｜a｜f（x）≤｜a＋b｜＋｜a－b｜恒成立，就有｜a｜f（x）≤2|a｜，所以，f（x）≤2，画出f（x）＝｜x－2｜的图象，如右图，当f（x）≤2，时有0≤x≤4。‎ ‎14、（2012烟台二模）已知向量且，若变量x,y满足约束条件，则z的最大值为 ‎15、（2012滨州二模）设x，y满足约束条件 ‎，若目标函数z＝ax＋by（a＞0，b＞0）的最大值为12，则的最小值为 ‎（A）　　（B）　　（C）　　（D）4　‎ 答案：D 解析：画出不等式组的可行域，如右图所示，目标函数变为：‎ ‎，所直线及其平行线，由图可知，当直线经过点B时，目标函数取得最大值，求得B点坐标为（4,6），所以有‎4a＋6b＝12，即‎2a＋3b＝6，‎ ‎＝＝≥＝4，所以，选D。‎ ‎16、（2012德州二模）设x，y满足约束条件，若的最小值为，17、（2012德州一模）已知在平面直角坐标系上的区域D由不等式组 确定，若为区域D上的动点，点A的坐标为(2，3)，则的最大值为( )‎ ‎ A.5 B．‎10 C． 14 D．‎ 答案：C 解析：不等式组的可行域如图所示BCD区域，‎ ‎＝‎ ‎＝＝，所以就是求的最大值，当点M在D点时，最大，D（1,4），OA＝，OD＝，AD＝，，所以，＝，因此最大值为：＝14，故选C。‎ ‎18、（2012德州一模）不等式对任意实数恒成立，则实数的取值范围是 ．‎ 答案：［-1,4］‎ 解析：因为，即的最小值为4，原不等式写成：‎ ‎，则小于或等于的最小值，即：‎ ‎≤4，解得。‎ ‎19、（2012临沂3月模拟）不等式的解集为___________；‎ ‎20、（2012青岛二模）设、满足约束条件，则目标函数的最大值为 .‎ ‎【答案】‎ ‎【解析】目标函数几何意义为区域内动点P到原点的距离的平方，做出图象如图 ‎，由图象可知当点P在C点时到原点的距离最大，由，得此时C点坐标为，所以。‎ ‎【2012安徽省合肥市质检理】设，若恒成立，则k的最大值为 ；‎ ‎【山东省微山一中2012届高三模拟理】5．若x，y满足约束条件，则目标函数的最大值是 （ ）‎ A．－3 B． C． 2 D．3‎ 答案D 解析:该题通过由约束条件，求目标函数的最大值简单考查线性规划求最优解问题;只要画出可行域即可看出最优解.‎ ‎【山东省潍坊市三县2012届高三模拟理】6．设0＜b＜a＜1,则下列不等式成立的是 （ ）‎ A．ab＜b2＜1 B．b＜a＜‎0 C．2b＜‎2a＜2 D．a2＜ab＜1‎ ‎【答案】C ‎【解析】因为b＜a＜1,所以2b＜‎2a <1,故选C.‎ ‎【山东省日照市2012届高三12月月考理】（11）如果不等式组表示的平面区域是一个直角三角形，则该三角形的面积为 ‎（A） （B） （C） （D）‎ ‎【山东实验中学2012届高三第四次诊断性考试理】10. 设x、y满足约束条件，若目标函数（其中)的最大值为3,则的最小值为（）‎ ‎(A) . 3 (B) . 1 (C) .2 (D) . 4‎ ‎【答案】A ‎【解析】解：如图所示，线性规划区域为三角形ABC，而目标函数的斜率为<0，‎ 因此目标函数的最大值即为过点B（1,2）取得。所以有a+2b=3, ‎ ‎（当且仅当a=b=1时，等号成立），故的最小值为3‎ ‎【山东省潍坊市三县2012届高三联考理】‎ ‎【2012唐山市高三模拟统一考试理】已知变量x，y满足约束条件则的最大值为 。‎ ‎【答案】 2 ‎ ‎【解析】本题主要考查线性规划的最优解. 属于基础知识、基本运算的考查.‎ 实数x，y满足不等式组则可行域如图，作出，平移，当直线通过A(1,0)时， 的最小值是⒉. ‎ ‎【2012年西安市高三年级第三次质检理】在平面直角坐标系xOy上的区域D由不等式组给定.若M(x ,y)为D上的动点，点N的坐标为（，1)，则的最大值为. _______‎ ‎【答案】4‎ ‎【解析】本题主要线性规划可行域的概念、平面向量的数量积. 属于基础知识、基本运算的考查.‎ ‎【2012年西安市高三年级第四次质检理】不等式|x+1| + |x-1|<3的实数解为_______‎ ‎【答案】‎ ‎【解析】本题主要考查. 属于基础知识、基本运算的考查.‎ 法1 由绝对值的意义，分别表示数轴上的点到1，-1的距离。由图知，时符合|x+1| + |x-1|<3‎ ‎∴不等式|x+1| + |x-1|<3的解集为 法2 列表法 ‎（--1）‎ ‎(-1,1)‎ ‎（1，+）‎ ‎1-‎ ‎1-‎ ‎-1‎ ‎-1-‎ ‎+1‎ ‎+1‎ ‎|x+1| + |x-1|<3‎ ‎-2<3‎ ‎2<3‎ ‎2<3‎ ‎-1>>‎ ‎ -1<<1‎ ‎1<<‎ ‎∴不等式|x+1| + |x-1|<3的解集为 ‎【2012江西师大附中高三模拟理】不等式的解集是（ ）‎ A． B． C． D． ‎ ‎【2012江西师大附中高三模拟理】设变量满足约束条件：的最大值为( ) ‎ A．10 B．‎8 ‎　 C．6 D．4‎ ‎【答案】B ‎【解析】本题主要考查线性规划的最优问题. 属于基础知识、基本运算的考查.‎ 如图，作出变量满足约束条件可行域是三角形ABC；A(-2,2),B(-2,-2)作出直线,‎ ‎,考虑直线 在y轴上截距的绝对值，由图知直线过A点时有最大值8‎ ‎【2012厦门市高三模拟质检理】若实数x，y满足不等式组 ，则：z＝2x + y的最小值为 A.－2　　　　　　B‎.1　‎　　　　　　C.4　　　　　　　D. 2‎ ‎【答案】B ‎ ‎【解析】本题主要考查线性规划的最优解问题. 属于基础知识、基本运算的考查.‎ 作出约束条件的可行域，如右的阴影部分，作出辅助直线 y＝2x，平移，易知直线过A时，z＝2x + y的最小值为1‎ ‎【2012厦门模拟质检理12】若变量x,y满足约束条件，则z＝2x－y的最大值等于　　　　　。‎ ‎【2012浙江宁波市模拟理】已知实数满足，若是使得取得最小值的可行解，则实数的取值范围为 .‎ ‎【2012安徽省合肥市质检理】已知满足，且z的最大值是最小值的4倍，则m的值是 （ ）‎ ‎ A． B． C． D．‎ ‎【答案】D ‎【解析】画出可行域可知，如图，‎ 最大值在点取得，最小值在点取得，由，解得。‎ ‎【2012山东青岛市模拟理】变量，满足，目标函数，则有　‎ A．无最大值 B．无最小值 C． D．既无最大值，也无最小值 ‎【2012山东青岛市模拟理】已知点在直线上，则的最小值为 . ‎ ‎【答案】‎ ‎【解析】因，所以（取等条件当且仅当）。‎ ‎【2012江西南昌市调研理】不等式的解集是 ( )‎ A．(1,+∞) B．[1,+∞) C．(-∞,0)∪[1,+∞) D．(-∞,0)∪(1,+∞)‎ ‎【2012广东佛山市质检理】已知不等式组， 表示的平面区域的面积为，点在所给平面区域内，则的最大值为 . ‎ ‎【答案】‎ ‎【解析】画出可行域得 故可行域的面积，解得，做目标直线，平移可知，在点处。‎ ‎【2012河南郑州市质检理】若实数的最小值是（ ）‎ A．0 B. ‎1 C. D. 9‎ ‎【答案】B ‎【解析】由题可知，的最小值，即的最小值，画出可行域，可得在点处取最小值0，即，选B。‎ ‎【2012北京海淀区模拟理】若实数满足 则的最大值为 . ‎ ‎【答案】7‎ ‎【解析】画出可行域得 由图可知，在点处取最大值为7.‎ ‎【2012宁德质检理12】已知实数x，y满足则的最大值 为 。‎ ‎【2012深圳中学模拟理9】已知实数、满足，则－3的最大值是 .‎ ‎【答案】-1‎ ‎【解析】解：作出不等式组表示的平面区域如图：‎ 作直线l: x－3y=0, 平移直线l，当直线l经过4x+y－9=0与x－y－1=0的交点P(2, 1)时，目标函数z=x－3y取得最大值z=2－3×1=－1,∴x－3y的最大值为－1.‎ ‎【2012海南嘉积中学模拟理11】某企业准备投资A、B两个项目建设，资金来源主要靠企业自筹和银行贷款两份资金构成，具体情况如下表。投资A项目资金不超过160万元，B项目不超过200万元，预计建成后，自筹资金每份获利12万元，银行贷款每份获利10万元，为获得总利润最大，那么两份资金分别投入的份数是（ ）‎ ‎ 单位：万元 ‎ 项目 自筹每份资金 银行贷款每份资金 A ‎20‎ ‎30‎ B ‎40‎ ‎30‎ A、自筹资金4份，银行贷款2份 B、自筹资金3份，银行贷款3份 C、自筹资金2份，银行贷款4份 D、自筹资金2份，银行贷款2份 ‎【2012黑龙江绥化市一模理15】已知实数，满足，如果目标函数的最小值为-1，则实数___.‎ ‎【答案】5 ‎ ‎ 【解析】作出的可行域，当时的最小值为-1，解；‎ ‎【2012 浙江瑞安模拟质检理6】若关于的不等式组表示的区域为三角形，则实数的取值范围是( ) ‎ A． B． C． D．‎ ‎【答案】C ‎【解析】由得M（1,1），因为不等式组表示的区域为三角形，所以 ‎【2012·泉州四校二次联考理12】若变量满足约束条件，则 的最小值为_______．‎ ‎【2012黄冈市高三上学期模拟考试理】不等式的解集为 。‎ ‎【答案】 （-0）（3，+）‎ ‎【解析】本题主要考查. 属于基础知识、基本运算的考查.‎ 法1 由绝对值的意义，分别表示数轴上的点到1，2的距离。由图知，时符合 ‎∴不等式的解集为（-0）（3，+）‎ 法2 列表法 ‎（-1）‎ ‎(1,2)‎ ‎（2，+）‎ ‎1-‎ ‎-1‎ ‎-1‎ ‎2-‎ ‎2-‎ ‎-2‎ ‎4->3‎ ‎2>3‎ ‎2-4>3‎ ‎<0‎ 无解 ‎>3‎ ‎∴不等式的解集为（-0）（3，+）‎ ‎【2012年石家庄市高中毕业班教学质检1理】设实数x，y满足不等式组，则的最小值是 ．‎ ‎【2012厦门市高三模拟质检理】已知函数f(x)＝　，则不等式f(x)＞f (1)的解集是　　 　　。‎ ‎【2012金华十校高三模拟联考理】已知实数x，y满足不等式组，则目标函数的最大值是 。‎ ‎【答案】 4‎ ‎【解析】本题主要考查线性规划的最优解问题. 属于基础知识、基本运算的考查.‎ ‎ 实数x，y满足不等式组则可行域如图，作出，平移，当直线通过A(2,2)时， 的最小值是4. ‎ ‎【2012唐山市高三模拟统一考试理】已知的解集为M。‎ ‎ （1）求M；‎ ‎ （2）当时，证明：‎ ‎【山东省滨州市沾化一中2012届高三模拟理】‎ ‎18．（本题满分12分）解关于x的不等式 ‎【答案】18．（本小题满分12分）‎ 解：原不等式等价于…………1分 当=0时，原不等式等价于 ……………2分 解得，此时原不等式得解集为{x|}； ……………3分 当>0时, 原不等式等价于, ……………4分 当原不等式的解集为； ……………5分 当0<原不等式的解集为； ……………6分 当原不等式的解集为； ……………7分 当<0时, 原不等式等价于， ……………8分 当时, 原不等式的解集为； ……………9分