人教版高三数学总复习课时作业14 9页

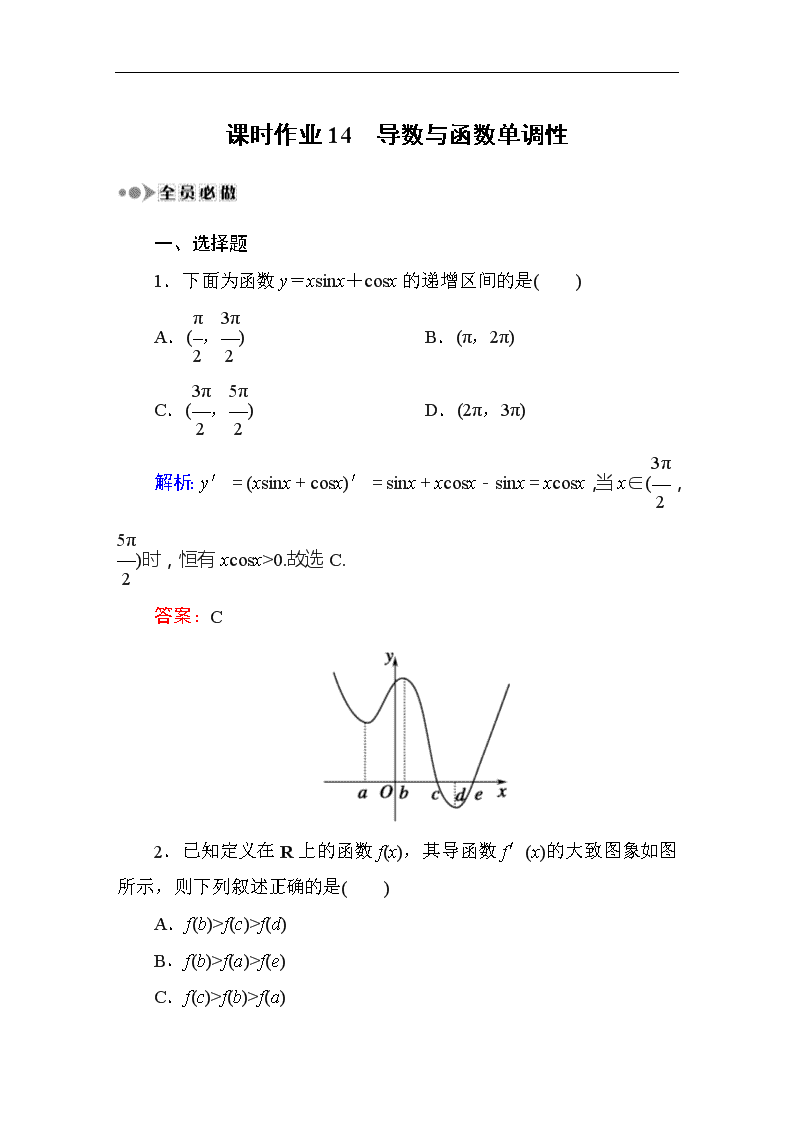
课时作业14　导数与函数单调性 一、选择题 ‎1．下面为函数y＝xsinx＋cosx的递增区间的是(　　)‎ A．(，) B．(π，2π)‎ C．(，) D．(2π，3π)‎ 解析：y′＝(xsinx＋cosx)′＝sinx＋xcosx－sinx＝xcosx，当x∈(，)时，恒有xcosx>0.故选C.‎ 答案：C ‎2．已知定义在R上的函数f(x)，其导函数f′(x)的大致图象如图所示，则下列叙述正确的是(　　)‎ A．f(b)>f(c)>f(d)‎ B．f(b)>f(a)>f(e)‎ C．f(c)>f(b)>f(a)‎ D．f(c)>f(e)>f(d)‎ 解析：依题意得，当x∈(－∞，c)时，f′(x)>0；当x∈(c，e)时，‎ f′(x)<0；当x∈(e，＋∞)时，f′(x)>0.因此，函数f(x)在(－∞，c)上是增函数，在(c，e)上是减函数，在(e，＋∞)上是增函数，又af(b)>f(a)．‎ 答案：C ‎3．∀x1，x2∈(0，)，x2>x1，y1＝，y2＝，则(　　)‎ A．y1＝y2‎ B．y1>y2‎ C．y1y2.‎ 答案：B ‎4．设函数f(x)＝x2－9lnx在区间[a－1，a＋1]上单调递减，则实数a的取值范围是(　　)‎ A．10)，‎ 当x－≤0时，有00且a＋1≤3，解得1f(b) B．f(a)＝f(b)‎ C．f(a)1‎ 解析：f′(x)＝，当x>e时，f′(x)<0，则f(x)在(e，＋∞)上为减函数，f(a)>f(b)．‎ 答案：A 二、填空题 ‎7．函数f(x)＝1＋x－sinx在(0,2π)上的单调情况是________．‎ 解析：在(0,2π)上有f′(x)＝1－cosx>0，所以f(x)在(0,2π)上单调递增．‎ 答案：单调递增 ‎8．若函数f(x)＝x3－x2＋ax＋4恰在[－1,4]上单调递减，则实数a的值为________．‎ 解析：∵f(x)＝x3－x2＋ax＋4，∴f′(x)＝x2－3x＋a，又函数f(x)恰在[－1,4]上单调递减，∴－1,4是f′(x)＝0的两根，∴a＝(－1)×4＝－4.‎ 答案：－4‎ ‎9．若函数f(x)＝(a>0)为R上的单调函数，则a的取值范围为________．‎ 解析：若f(x)为R上的单调函数，则f′(x)在R上不变号，结合f′(x)＝ex与条件a>0，知ax2－2ax＋1≥0在R上恒成立，因此Δ＝‎4a2－‎4a＝‎4a(a－1)≤0，由此并结合a>0，知00)，则h′(x)＝－－<0，即h(x)在(0，＋∞‎ ‎)上是减函数．‎ 由h(1)＝0知，当00，从而f′(x)>0；‎ 当x>1时，h(x)<0，从而f′(x)<0.‎ 综上可知，f(x)的单调递增区间是(0,1)，单调递减区间是(1，＋∞)．‎ ‎11．已知函数f(x)＝x3－ax2－3x.‎ ‎(1)若f(x)在[1，＋∞)上是增函数，求实数a的取值范围；‎ ‎(2)若x＝3是f(x)的极值点，求f(x)的单调区间．‎ 解：(1)对f(x)求导，得f′(x)＝3x2－2ax－3.‎ 由f′(x)≥0，得a≤.‎ 记t(x)＝，当x≥1时，t(x)是增函数，‎ ‎∴t(x)min＝(1－1)＝0.∴a≤0.‎ ‎(2)由题意，得f′(3)＝0，即27－‎6a－3＝0，‎ ‎∴a＝4.∴f(x)＝x3－4x2－3x，‎ f′(x)＝3x2－8x－3.‎ 令f′(x)＝0，得x1＝－，x2＝3.‎ 当x变化时，f′(x)、f(x)的变化情况如下表：‎ x ‎－ ‎3‎ ‎(3，＋∞)‎ f′(x)‎ ‎＋‎ ‎0‎ ‎－‎ ‎0‎ ‎＋‎ f(x)‎ 极大值 极小值 ‎∴f(x)的单调递增区间为，[3，＋∞)，f(x ‎)的单调递减区间为.‎ ‎1．函数f(x)＝x2－2ax＋a在区间(－∞，1)上有最小值，则函数g(x)＝在区间(1，＋∞)上一定(　　)‎ A．有最小值 B．有最大值 C．是减函数 D．是增函数 解析：由函数f(x)＝x2－2ax＋a在区间(－∞，1)上有最小值，可得a<1，又g(x)＝＝x＋－‎2a，则g′(x)＝1－，易知在x∈(1，＋∞)上g′(x)>0，所以g(x)在(1，＋∞)上为增函数．‎ 答案：D ‎2．已知f(x)为R上的可导函数，且∀x∈R，均有f(x)>f′(x)，则以下判断正确的是(　　)‎ A．f(2 013)>e2 ‎013f(0)‎ B．f(2 013)f′(x)，∴g′(x)<0，即函数g(x)在R上递减，∴g(2 013)0，函数f(x)在(0，＋∞)上单调递增，‎ 当a<0时，令g(x)＝ax2＋(‎2a＋2)x＋a，‎ 由于Δ＝(‎2a＋2)2－‎4a2＝4(‎2a＋1)．‎ ‎①当a＝－时，Δ＝0，‎ f′(x)＝≤0，函数f(x)在(0，＋∞)上单调递减．‎ ‎②当a<－时，Δ<0，g(x)<0，‎ f′(x)<0，函数f(x)在(0，＋∞)上单调递减．‎ ‎③当－0，‎ 设x1，x2(x10，‎ 所以x∈(0，x1)时，g(x)<0，f′(x)<0，函数f(x)单调递减，‎ x∈(x1，x2)时，g(x)>0，f′(x)>0，函数f(x)单调递增，‎ x∈(x2，＋∞)时，g(x)<0，f′(x)<0，函数f(x)单调递减．‎ 综上可得：‎ 当a≥0时，函数f(x)在(0，＋∞)上单调递增；‎ 当a≤－时，函数f(x)在(0，＋∞)上单调递减；‎ 当－