2020年佛山市普通高中教学质量检测（一）文数试题 4页

高三教学质量检测（一）文科数学试题 第 1 页 共 4 页 2019～2020 学年佛山市普通高中高三教学质量检测（一） 数 学(文科) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分 150 分．考试时间 120 分钟． 注意事项： 1．答卷前，考生要务必填写答题卷上的有关项目． 2．选择题每小题选出答案后，用 2B 铅笔把答案涂在答题卷相应的位置上． 3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内；如需改 动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液，不按以上要求作答的答案无效． 4．请考生保持答题卷的整洁．考试结束后，将答题卷交回． 第Ⅰ卷(选择题 共 60 分) 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只有一项是符合题 目要求的． 1．在复平面内，复数 5 1 2i 对应的点位于（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 2．已知集合  2 2 0A x x x   ，  1 1B x x    ，则 A B I （ ） A． ( 1,1) B． ( 1,2) C． ( 1,0) D． (0,1) 3．已知 ,x y R ，且 0x y  ，则（ ） A． cos cos 0x y  B． cos cos 0x y  C． ln ln 0x y  D． ln ln 0x y  4．函数 ( )f x 的图像向右平移一个单位长度，所得图像与 exy  关于 x 轴对称，则 ( )f x  （ ） A． 1ex B． 1ex C． 1e x  D． 1e x  5．已知函数    22 ln ( )f x x x a x a     R 为奇函数，则 a  （ ） A． 1 B． 0 C．1 D． 2 6．希尔宾斯基三角形是一种分形，由波兰数学家希尔宾斯基在 1915 年提出，先作一个正三角形，挖去一 个“中心三角形”（即以原三角形各边的中点为顶点的三角形），然后在剩下的小三角形中又挖去一个 “中心三角形”，我们用白色代表挖去的 面积，那么黑三角形为剩下的面积（我 们称黑三角形为希尔宾斯基三角形）．在 如图第 3 个大正三角形中随机取点，则 落在黑色区域的概率为（ ） A． 3 5 B． 9 16 C． 7 16 D． 2 5 7．已知 为锐角， 3cos 5   ，则 πtan =4 2     （ ） A． 1 3 B． 1 2 C． 2 D．3 2020 年 1 月 高三教学质量检测（一）文科数学试题 第 2 页 共 4 页 8．“砸金蛋”（游玩者每次砸碎一颗金蛋，如果有奖品，则“中奖”）是现在商家一种常见促销手段．今年 “双十一”期间，甲、乙、丙、丁四位顾客在商场购物时，每人均获得砸一颗金蛋的机会．游戏开始 前，甲、乙、丙、丁四位顾客对游戏中奖结果进行了预测，预测结果如下： 甲说：“我或乙能中奖”； 乙说：“丁能中奖”； 丙说：“我或乙能中奖”； 丁说：“甲不能中奖”． 游戏结束后，这四位同学中只有一位同学中奖，且只有一位同学的预测结果是正确的，则中奖的同学是 （ ） A．甲 B．乙 C．丙 D．丁 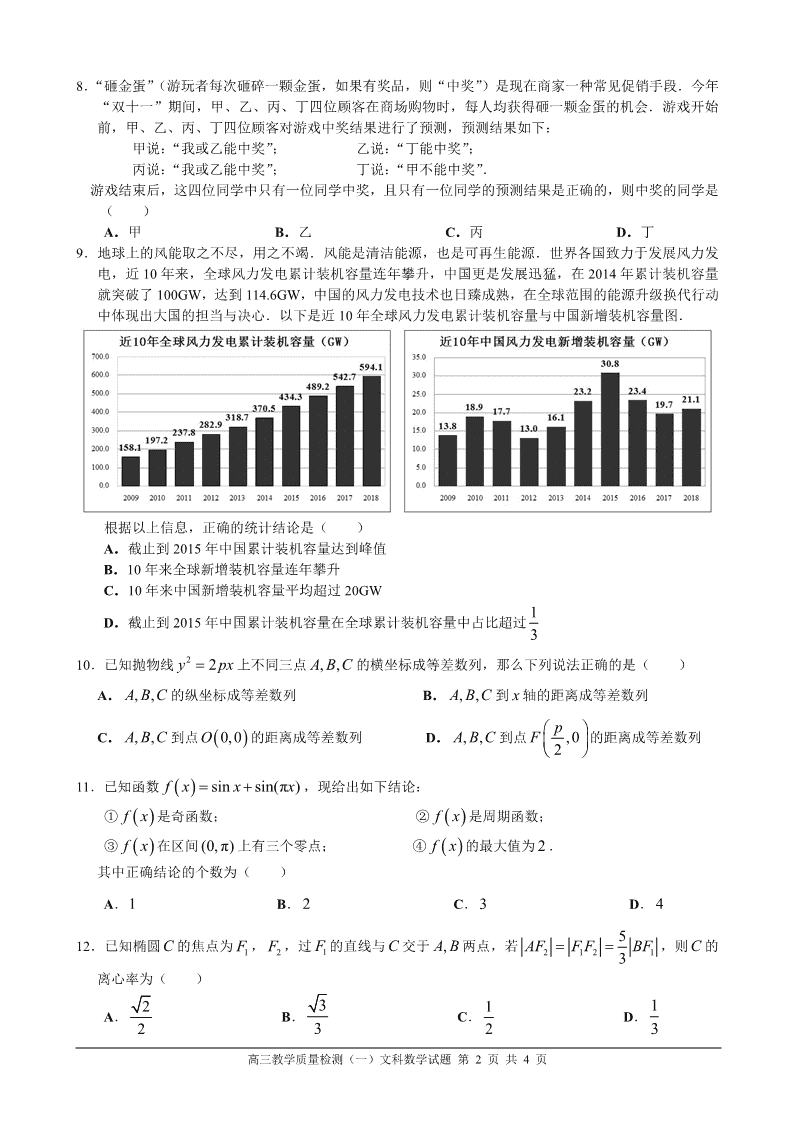9．地球上的风能取之不尽，用之不竭．风能是清洁能源，也是可再生能源．世界各国致力于发展风力发 电，近 10 年来，全球风力发电累计装机容量连年攀升，中国更是发展迅猛，在 2014 年累计装机容量 就突破了 100GW，达到 114.6GW，中国的风力发电技术也日臻成熟，在全球范围的能源升级换代行动 中体现出大国的担当与决心．以下是近 10 年全球风力发电累计装机容量与中国新增装机容量图． 根据以上信息，正确的统计结论是（ ） A．截止到 2015 年中国累计装机容量达到峰值 B．10 年来全球新增装机容量连年攀升 C．10 年来中国新增装机容量平均超过 20GW D．截止到 2015 年中国累计装机容量在全球累计装机容量中占比超过 1 3 10．已知抛物线 2 2y px 上不同三点 , ,A B C 的横坐标成等差数列，那么下列说法正确的是（ ） A． , ,A B C 的纵坐标成等差数列 B． , ,A B C 到 x 轴的距离成等差数列 C． , ,A B C 到点  0,0O 的距离成等差数列 D． , ,A B C 到点 ,02 pF      的距离成等差数列 11．已知函数   sin sin(π )f x x x  ，现给出如下结论： ①  f x 是奇函数； ②  f x 是周期函数； ③  f x 在区间 (0, π) 上有三个零点； ④  f x 的最大值为 2 ． 其中正确结论的个数为（ ） A．1 B． 2 C．3 D． 4 12．已知椭圆C 的焦点为 1F ， 2F ，过 1F 的直线与 C 交于 ,A B 两点，若 2 1 2 1 5 3AF F F BF  ，则C 的 离心率为（ ） A． 2 2 B． 3 3 C． 1 2 D． 1 3 高三教学质量检测（一）文科数学试题 第 3 页 共 4 页 第Ⅱ卷(非选择题 共 90 分) 本卷包括必考题和选考题两部分．第 13～21 题为必考题，每个试题考生都必须作答．第 22～23 为选 考题，考生根据要求作答． 二、填空题：本大题共 4 小题，每小题 5 分，满分 20 分． 13．函数 ( ) e sinxf x x  在点 0,1 处的切线方程为 ． 14．若实数变量 ,x y 满足约束条件 1 1 y x x y y        ，且 2z x y  的最大值和最小值分别为 m 和 n ，则 m n  ． 15．在△ ABC 中， 1a  ， 3cos 4C  ，△ ABC 的面积为 7 4 ，则 c  ． 16．已知正三棱柱 1 1 1ABC A B C 的侧棱长为 ( )m mZ ，底面边长为 ( )n nZ ，内有一个体积为V 的球， 若V 的最大值为 9 π2 ，则此三棱柱外接球表面积的最小值为 ． 三、解答题：本大题共 7 小题，共 70 分，解答须写出必要的文字说明、证明过程或演算步骤． 17．(本小题满分 12 分) 已知数列 na 是等比数列，数列 nb 满足 1 2 1 2b b  ， 3 3 8b  ， 1 1 2 1n n n na b b    ． （1）求 na 的通项公式； （2）求 nb 的前 n 项和． 18．(本小题满分 12 分) 党中央、国务院历来高度重视青少年的健康成长．“少年强则国强”，青少年身心健康、体魄强健、意 志坚强、充满活力，是一个民族旺盛生命力的体现，是社会文明进步的标志，是国家综合实力的重要方面．全 面实施《国家学生体质健康标准》，把健康素质作为评价学生全面健康发展的重要指标，是新时代的要 求．《国家学生体质健康标准》有一项指标是学生体质指数（BMI），其计算公式为： 2 2 (kg)BMI (m )  体重 身高 ， 当 BMI 23.5 时，认为“超重”，应加强锻炼以改善 BMI． 某高中高一、高二年级学生共 2000 人，人数分布如表(a)． 为了解这 2000 名学生的 BMI 指数情况，从中随机抽取容量为 160 的一个样本． （1）为了使抽取的 160 个学生更具代表性，宜采取分层 抽样，试给出一个合理的分层抽样方案，并确定每层应抽取出的学生人数； （2）分析这 160 个学生的 BMI 值，统计出“超重”的学生人数分布如表(b)． （i）试估计这 2000 名学生中“超重”的学生数； （ii）对于该校的 2000 名学生，应用独立性检验的知识，可分 析出性别变量与年级变量哪一个与“是否超重”的关联性更强．应 用卡方检验，可依次得到 2K 的观测值 1k ， 2k ，试判断 1k 与 2k 的大 小关系．（只需写出结论） 性别 年级 男生 女生 合计 高一年级 550 650 1200 高二年级 425 375 800 合计 975 1025 2000 表(a) 性别 年级 男生 女生 高一年级 4 6 高二年级 2 4 表(b) 高三教学质量检测（一）文科数学试题 第 4 页 共 4 页 19．(本小题满分 12 分) 如图，三棱锥 P ABC 中， PA PB PC  ， 90APB ACB     ，点 ,E F 分别是棱 ,AB PB 的 中点，点 G 是△ BCE 的重心． （1）证明： PE  平面 ABC ； （2）若 GF 与平面 ABC 所成的角为 60 ，且 2GF  ， 求三棱锥 P ABC 的体积． 20．(本小题满分12分) 在平面直角坐标系 xOy 中，已知两定点 ( 2,2)A  ， (0,2)B ，动点 P 满足 | | 2| | PA PB  ． （1）求动点 P 的轨迹C 的方程； （2）轨迹C 上有两点 ,E F ，它们关于直线 : 4 0l kx y   对称，且满足 4OE OF  uuur uuur ，求△OEF 的 面积． 21．(本小题满分12分) 已知函数 ( ) 1 2 sin e xf x a x    ， ( )f x 是 ( )f x 的导函数，且 (0) 0f   ． （1）求 a 的值，并证明 ( )f x 在 0x  处取得极值； （2）证明： ( )f x 在区间 π2 π,2 π ( )2k k k     N 有唯一零点． 请考生在第 22，23 题中任选一题做答，如果多做，则按所做的第一题计分，做答时请写清楚题号． 22．(本小题满分 10 分)[选修 4 4 :坐标系与参数方程选讲] 在直角坐标系 xOy 中，曲线C 的参数方程为 24 4 x m y m     ( m 为参数)． （1）写出曲线C 的普通方程，并说明它表示什么曲线； （2）已知倾斜角互补的两条直线 1l ， 2l ，其中 1l 与C 交于 A ， B 两点， 2l 与C 交于 M ， N 两点， 1l 与 2l 交于点  0 0,P x y ，求证： PA PB PM PN   ． 23．(本小题满分 10 分)[选修 4 5 :不等式选讲] 已知函数 ( ) 1f x x a x    ． （1）若 ( ) 2f a  ，求 a 的取值范围； （2）当 [ , ]x a a k  时，函数 ( )f x 的值域为[1,3]，求 k 的值．