甘肃省兰州市联片办学2019-2020学年高一上学期期末考试数学试卷 含解析 16页

‎2019-2020学年度第一学期期末考试 高一年级数学试卷 一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1. 直线经过原点和点(－1，－1)，则它的倾斜角是(　　)‎ A. 45° B. 135°‎ C. 45°或135° D. 0°‎ ‎【答案】A ‎【解析】‎ 先由已知的两点坐标求出过两点直线方程的斜率，然后利用直线的斜率等于倾斜角的正切值，再利用特殊角的三角函数值及倾斜角的范围即可得到倾斜角的度数．‎ 解：设过原点（0，0）和点（-1，-1）的直线方程的斜率为k，且该直线的倾斜角为α，‎ 由题意可知：tanα=k==1，又α∈（0，180°），‎ 则α=45°．‎ 故选A ‎2.下列命题正确的是（ ）‎ A. 若直线平面，直线平面，则 B. 若直线上有两个点到平面的距离相等，则 C. 直线l与平面所成角取值范围是 D. 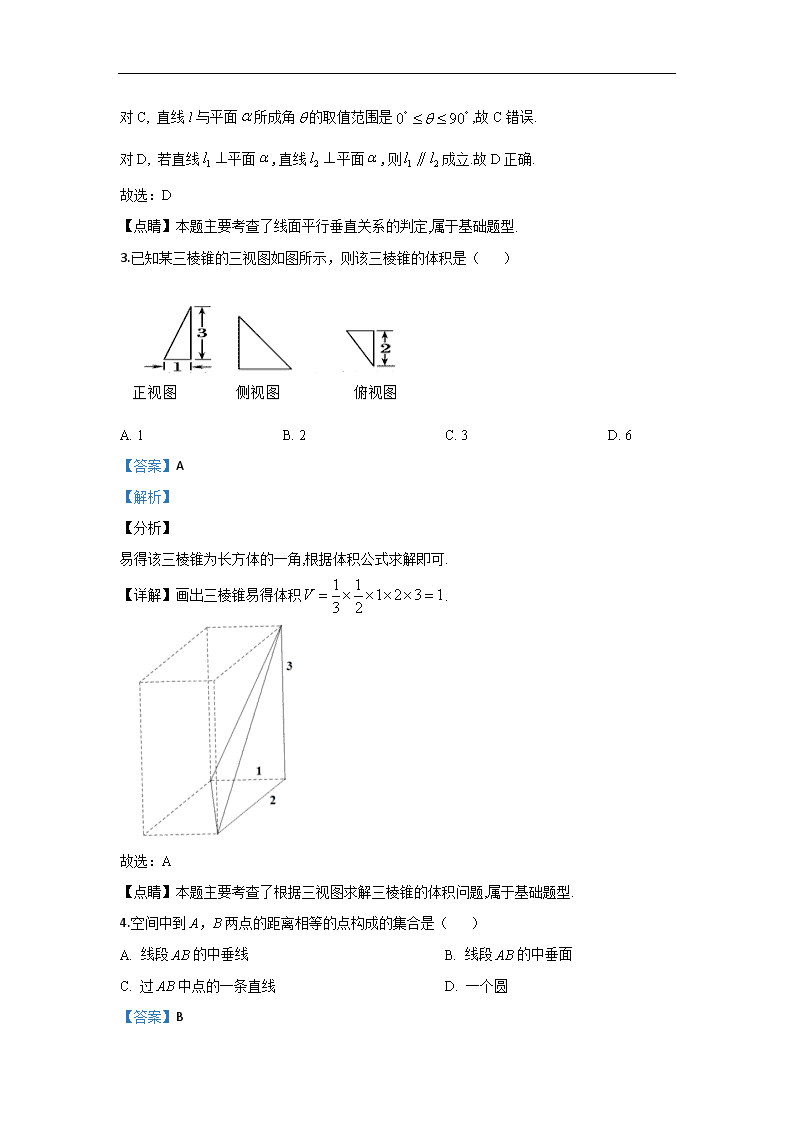若直线平面，直线平面，则 ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据线面平行垂直的性质与判定判断即可.‎ ‎【详解】对A, 若直线平面,直线平面,不一定有,故A错误.‎ 对B,当平面时也满足直线上有两个点到平面的距离相等.故B错误.‎ 对C, 直线l与平面所成角的取值范围是,故C错误.‎ 对D, 若直线平面,直线平面,则成立.故D正确.‎ 故选：D ‎【点睛】本题主要考查了线面平行垂直关系的判定,属于基础题型.‎ ‎3.已知某三棱锥的三视图如图所示，则该三棱锥的体积是（ ）‎ A. 1 B. ‎2 ‎C. 3 D. 6‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 易得该三棱锥为长方体的一角,根据体积公式求解即可.‎ ‎【详解】画出三棱锥易得体积.‎ 故选：A ‎【点睛】本题主要考查了根据三视图求解三棱锥的体积问题,属于基础题型.‎ ‎4.空间中到A，B两点的距离相等的点构成的集合是（ ）‎ A. 线段AB的中垂线 B. 线段AB的中垂面 C. 过AB中点的一条直线 D. 一个圆 ‎【答案】B ‎【解析】‎ ‎【分析】‎ 直观想象求解即可.‎ ‎【详解】空间中到A,B两点的距离相等的点构成的集合是线段AB的中垂面.‎ 故选：B ‎【点睛】本题主要考查了空间想象能力,属于基础题型.‎ ‎5.设长方体的对角线长是4，过每一顶点有两条棱与对角线的夹角都是，则此长方体的体积是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 画图再设过某一顶点的两条棱与对角线的夹角都是再求棱长即可.‎ ‎【详解】由题画出图像,可设与对角线的夹角为.因为,故,同理,又可得.故长方体的体积为.‎ 故选：B ‎【点睛】本题主要考查了长方体中的线线夹角以及棱长与对角线的关系等.属于基础题型.‎ ‎6.已知点A、B、C、D为同一球面上的四点，且，则这个球的表面积是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 易得三棱锥为正方体的一角,再求正方体的体对角线与外接球表面积即可.‎ ‎【详解】易得三棱锥为正方体的一角,且体对角线为外接球的直径,‎ 故.故外接球的表面积.‎ 故选：C ‎【点睛】本题主要考查了正方体中的一角三棱锥与外接球的表面积,属于基础题型.‎ ‎7.已知直线：与：平行，则的值是（ ）.‎ A. 或 B. 或 C. 或 D. 或 ‎【答案】C ‎【解析】‎ 当k-3=0时，求出两直线的方程，检验是否平行；当k-3≠0时，由一次项系数之比相等且不等于常数项之比，求出k的值．‎ 解：由两直线平行得，当k-3=0时，两直线的方程分别为 y=-1 和 ‎ y=3/2，显然两直线平行．当k-3≠0时，由，可得 k=5．综上，k的值是 3或5，‎ 故选 C．‎ ‎【此处有视频，请去附件查看】‎ ‎8.设是两个不同的平面，是一条直线，以下命题正确的是（ ）‎ A. 若，则 B. 若，则 C. 若，则 D. 若，则 ‎【答案】C ‎【解析】‎ 对于A、B、D均可能出现，而对于C是正确的．‎ ‎9.锐二面角，直线ABα，AB与l所成的角为45°，AB与平面β成30°角，则二面角的大小为(　　)‎ A. 30° B. 45° C. 60° D. 90°‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 如图，作AO⊥l于O，作AC⊥β于C，再求∠AOC的大小即得解.‎ ‎【详解】如图，作AO⊥l于O，作AC⊥β于C，连接BC，OC．在Rt△AOB中，∠ABO＝45°，设AB＝1，则AO＝．‎ ‎∵在Rt△ACB中，∠ABC＝30°，∴AC＝AB＝，‎ ‎∴在Rt△ACO中，sin∠AOC＝,∴∠AOC＝45°．‎ 所以二面角的大小为45°.故答案为B 点睛】‎ ‎(1)本题主要考查线面角和二面角的计算，意在考察学生对这些知识的掌握水平和分析推理能力.(2) 二面角的求法方法一：（几何法）找作（定义法、三垂线法、垂面法）证（定义）指求（解三角形）.方法二：（向量法）首先求出两个平面的法向量；再代入公式（其中分别是两个平面的法向量，是二面角的平面角.）求解.（注意先通过观察二面角的大小选择“”号）‎ ‎10.函数在区间内的零点的近似值（精确度0.1）是（ ）‎ A. 1.55 ‎B. ‎1.65 ‎C. 1.75 D. 1.85‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 易得函数在区间内的零点为判断即可.‎ ‎【详解】由题函数在区间内的零点为,四个选项中离1.75最近.‎ 故选：C ‎【点睛】本题主要考查了函数的零点问题.属于基础题型.‎ ‎11. 已知某几何体的三视图如右图所示，则该几何体的外接球表面积为（ ）‎ A. B. 32 C. D. ‎ ‎【答案】C ‎【解析】‎ 试题分析：由三视图知该几何体是底面是直角边为的等腰直角三角形，一条长为的侧棱与底面垂直的三棱锥，其外接球就是底边长为，高为的正四棱柱的外接球，设球半径为，则，故选C.‎ 考点：1、几何体的三视图；2、几何体的外接球体积.‎ ‎12.已知函数f（x）的定义域为（﹣∞，0）∪（0，+∞），f（x）是奇函数，且当x＞0时，f（x）=x2﹣x+a，若函数g（x）=f（x）﹣x的零点恰有两个，则实数a的取值范围是（ ）‎ A. a＜0 B. a≤‎0 ‎C. a≤1 D. a≤0或a=1‎ ‎【答案】D ‎【解析】‎ 试题分析：要使函数g（x）=f（x）﹣x的零点恰有两个，则根据函数是奇函数，则只需要当x＞0时，函数g（x）=f（x）﹣x的零点恰有一个即可．‎ 解：因为f（x）是奇函数，所以g（x）=f（x）﹣x也是奇函数，‎ 所以要使函数g（x）=f（x）﹣x的零点恰有两个，‎ 则只需要当x＞0时，函数g（x）=f（x）﹣x的零点恰有一个即可．‎ 由g（x）=f（x）﹣x=0得，g（x）=x2﹣x+a﹣x=x2﹣2x+a=0，‎ 若△=0，即4﹣‎4a=0，解得a=1．‎ 若△＞0，要使当x＞0时，函数g（x）只有一个零点，则g（0）=a≤0，‎ 所以此时，解得a≤0．‎ 综上a≤0或a=1．‎ 故选D．‎ 考点：函数的零点．‎ 二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中横线上）‎ ‎13.求满足的的取值集合是______________.‎ ‎【答案】(-2,4)‎ ‎【解析】‎ ‎【详解】因为 ‎14.一个直径为32厘米的圆柱形水桶中放入一个铁球，球全部没入水中后，水面升高9厘米，则此球的半径为_____厘米．‎ ‎【答案】12‎ ‎【解析】‎ 试题分析：‎ 考点：球的体积和表面积 ‎15.已知正四棱锥（底面是正方形且侧棱都相等）中，，是侧棱的中点，则异面直线与所成角的大小为　　　　　　　.‎ ‎【答案】‎ ‎【解析】‎ 设与相交于点，连接．因为是正方形，所以是中点．而是中点，所以，则是异面直线与所成角．因为是正四棱锥，所以面，从而可得面面．因为，所以面，从而．因为，所以，所以是等腰直角三角形，从而可得 ‎16.已知直线恒经过一个定点，则过这一定点和原点直线方程是_____________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 由直线，可得，从而可得定点坐标，进而可求直线方程.‎ ‎【详解】由直线，可得，‎ 令，可得，‎ 直线恒经过一个定点，‎ 过这一定点和原点的直线方程是，即.‎ 故答案为.‎ ‎【点睛】本题考查直线恒过定点，考查学生分析解决问题的能力，属于基础题.‎ 三、解答题（本大题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤）‎ ‎17.已知函数f(x)＝lg(3＋x)＋lg(3－x)．‎ ‎(1)求函数f(x)的定义域；‎ ‎(2)判断函数f(x)的奇偶性，并说明理由．‎ ‎【答案】（1）；（2）偶函数,理由详见解析 ‎【解析】‎ 试题分析：（1）求定义域，通常就是求使函数式有意义的自变量取值集合，所以只要满足各项都有意义即可，对数型的函数求值域，关键求出真数部分的取值范围就可以了；（2）判断函数奇偶性，就是利用奇偶性定义判断即可．‎ 试题解析：（1）由函数式可得 又 所以值域为 ‎（2）由（1）可知定义域关于原点对称 所以原函数为偶函数 ‎ 考点：1．求复合函数的定义域、值域；2．用定义判断函数奇偶性．‎ ‎18.如图所示，在四边形ABCD中，，，，，，求四边形ABCD绕AD旋转一周所形成的几何体的表面积及体积.‎ ‎【答案】.‎ ‎【解析】‎ ‎【详解】‎ 如图，过C作CE垂直于AD，交AD延长线于E，则所求几何 的体积可看成是由梯形ABCE绕AE旋转一周所得的圆台的体积，减去△EDC绕DE旋转一周所得的圆锥的体积．‎ 所以所求几何体的表面积=，体积V＝V圆台－V圆锥＝π×(52＋5×2＋22)×4－π×22×2＝π.‎ 点睛：本题考查了旋转体结构特征，以及旋转体的体积.解决本类问题时，首先要作出旋转体的直观图，仔细分析旋转体的结构特征，为顺利解题创造依据，这类问题对空间想象力，转化能力以及计算能力都有较高的要求，需要特别强化训练注意总结解题规律.‎ ‎19.已知四棱柱中，底面ABCD，且底面ABCD为菱形，F为的中点，M为线段的中点，‎ 求证:（1）平面ABCD;‎ ‎（2）平面.‎ ‎【答案】(1) 证明见解析(2) 证明见解析 ‎【解析】‎ ‎【分析】‎ ‎(1) 取AC的中点O,再证明即可.‎ ‎(2)利用等腰三角形与菱形的性质证明与即可.‎ ‎【详解】证明:（1）取AC的中点O,连接MO,‎ 因为M,O分别为,AC的中点,‎ 所以 又F为的中点,‎ 所以.‎ 所以.‎ 所以四边形MOBF为平行四边形.‎ 所以,又平面ABCD,平面ABCD,‎ 所以平面ABCD.‎ ‎（2）因为F为的中点,易得,‎ 又M为的中点,所以 又四边形ABCD为菱形,所以.‎ 又所以.‎ 又,所以平面.‎ ‎【点睛】本题主要考查了线面平行与线面垂直的判定与性质,属于中等题型.‎ ‎20.如图所示，在三棱柱中，与都为正三角形，且平面，分别是的中点.‎ 求证：（1）平面平面；‎ ‎（2）平面平面.‎ ‎【答案】(1)见解析.(2)见解析.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由分别是的中点，证得，由线面平行的判定定理，可得平面，平面，再根据面面平行的判定定理，即可证得平面平面.‎ ‎（2）利用线面垂直的判定定理，可得平面，再利用面面垂直的判定定理，即可得到平面平面.‎ ‎【详解】（1）在三棱柱中，‎ 因为分别是的中点，所以，‎ 根据线面平行的判定定理，可得平面，平面 又，‎ ‎∴平面平面.‎ ‎（2）在三棱柱中，平面，所以，‎ 又，，所以平面，‎ 而平面，所以平面平面.‎ ‎【点睛】本题考查线面位置关系的判定与证明，熟练掌握空间中线面位置关系的定义、判定、几何特征是解答的关键，其中垂直、平行关系证明中应用转化与化归思想的常见类型：(1)证明线面、面面平行，需转化为证明线线平行；(2)证明线面垂直，需转化为证明线线垂直；(3)证明线线垂直，需转化为证明线面垂直．‎ ‎21.已知点.‎ ‎（1）求过P点与原点距离最大的直线l的方程，最大距离是多少？‎ ‎（2）是否存在过P点与原点距离为6的直线？若存在，求出方程；若不存在，请说明理由.‎ ‎【答案】(1) ，最大距离是 (2) 不存在,见解析 ‎【解析】‎ ‎【分析】‎ ‎(1)作图可得当时直线l与原点距离最大,再根据垂直求解即可.‎ ‎(2)根据(1)中的结论判断即可.‎ ‎【详解】（1）作图可证过P点与原点O距离最大的距离是过P点且与PO垂直的直线,‎ 由,得,所以 由直线方程的点斜式得,‎ 即.‎ 即直线是过P点且与原点O距离最大的直线,最大距离为.‎ ‎（2）由（1）可得过P点且与原点O的最大距离为,因此不存在过点P点且到原点距离为6的直线.‎ ‎【点睛】本题主要考查了点与线的距离的最值问题,需要画图分析得时距离最大.属于基础题型.‎ ‎22.过点的直线被两平行线与截得的线段长，求直线的方程.‎ ‎【答案】.‎ ‎【解析】‎ ‎【详解】当直线的方程为时，可验证不符合题意，‎ 故设的方程为，‎ 由解得；‎ 由解得，‎ 因为，所以，‎ 整理得，解得或．‎ 直线方程为 考点：直线与直线的位置关系.‎