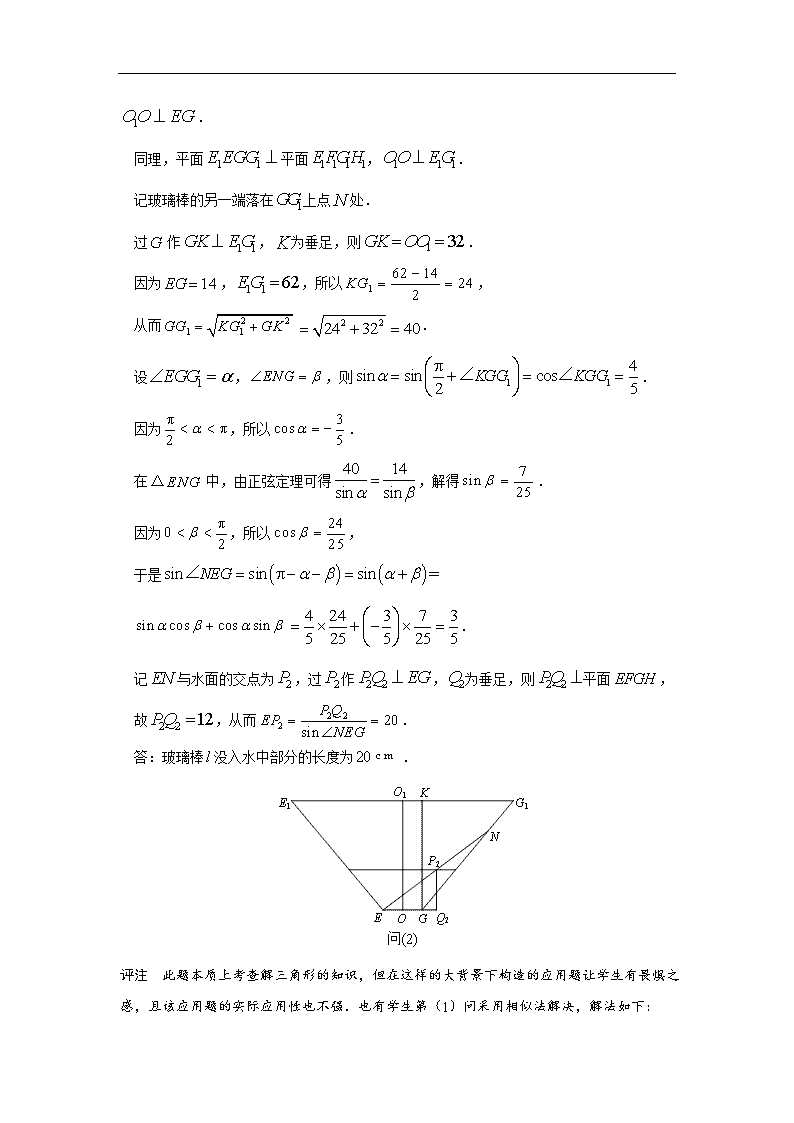2013-2017高考数学分类汇编-第8章 立体几何-3 空间点，直线，平面之间的位置关系（理科） 4页

第3节 空间点、直线、平面之间的位置关系 ‎1.已知直线，分别在两个不同的平面，内，则“直线和直线相交”是“平面和平面相 交”的（ ）.‎ A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 ‎1.A 解析 由直线和直线相交，可知平面有公共点，所以平面和平面相交．反过来，如果平面和平面相交，直线和直线不一定相交，可能与两平面的交线都平行.故选A.‎ 题型90 证明“点共面”“线共面”“点共线”或“线共点” ——暂无 ‎1. (2013安徽理3） 在下列命题中，不是公理的是（ ）.‎ A. 平行于同一个平面的两个平面相互平行 B. 过不在同一条直线上的三点，有且只有一个平面 ‎ C. 如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在此平面内 D. 如果两个不重合的平面有一个公共点，那么他们有且只有一条过该点的公共直线 ‎ 题型91 截面问题——暂无 ‎1. 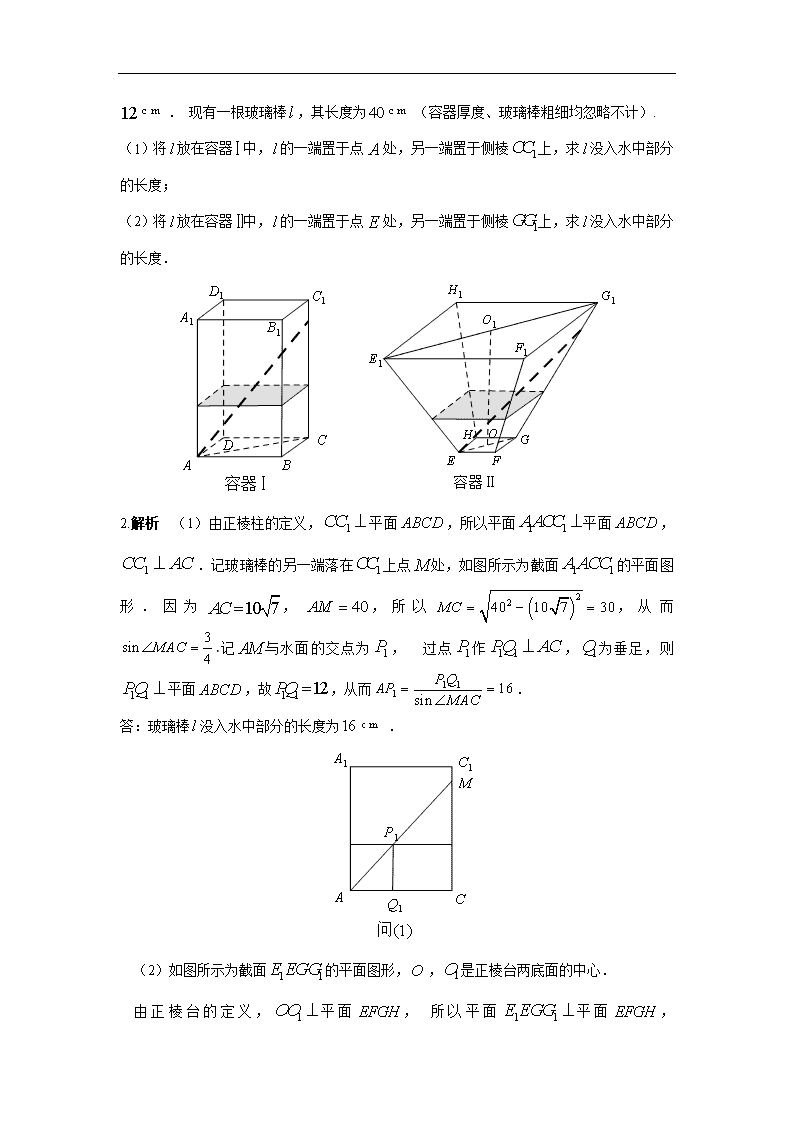(2013安徽理15） 如图，正方体的棱长为，为的中点，为线段上的动点，过点的平面截该正方体所得的截面记为.则下列命题正确的是 （写出所有正确命题的编号）‎ ①当时，为四边形 ②当时，为等腰梯形 ③当时，与的交点满足 ④当时，为六边形 ⑤当时，的面积为 ‎2.（2017江苏18）如图所示，水平放置的正四棱柱形玻璃容器和正四棱台形玻璃容器的高均为，容器的底面对角线的长为，容器的两底面对角线，的长分别为和． 分别在容器和容器中注入水，水深均为 ‎． 现有一根玻璃棒，其长度为（容器厚度、玻璃棒粗细均忽略不计）.‎ ‎（1）将放在容器中，的一端置于点处，另一端置于侧棱上，求没入水中部分 的长度；‎ ‎（2）将放在容器中，的一端置于点处，另一端置于侧棱上，求没入水中部分 的长度．‎ ‎ ‎ ‎2.解析 （1）由正棱柱的定义，平面，所以平面平面，．记玻璃棒的另一端落在上点处，如图所示为截面的平面图形．因为，，所以，从而.记与水面的交点为， 过点作，为垂足，则平面，故，从而．‎ 答：玻璃棒没入水中部分的长度为．‎ ‎（2）如图所示为截面的平面图形，，是正棱台两底面的中心．‎ 由正棱台的定义，平面， 所以平面平面，‎ ‎．‎ 同理，平面平面，．‎ 记玻璃棒的另一端落在上点处．‎ 过作，为垂足，则．‎ 因为，，所以，‎ 从而．‎ 设，，则．‎ 因为，所以．‎ 在中，由正弦定理可得，解得． ‎ 因为，所以，‎ 于是 ‎．‎ 记与水面的交点为，过作，为垂足，则平面，‎ 故，从而．‎ 答：玻璃棒没入水中部分的长度为．‎ 评注 此题本质上考查解三角形的知识，但在这样的大背景下构造的应用题让学生有畏惧之感，且该应用题的实际应用性也不强．也有学生第（1）问采用相似法解决，解法如下：‎ ‎，，所以，，‎ 所以由，，即，解得．‎ 答：玻璃棒没入水中部分的长度为．‎ 题型92 异面直线的判定——暂无 ‎1．（2015年广东理8）若空间中个不同的点两两距离都相等，则正整数的取值（ ）‎ A．至多等于 B．至多等于 C．等于 D．大于 ‎1.解析 正四面体的四个顶点两两距离相等，即空间中个不同的点两两距离都相等，‎ 则正整数可以等于4，而且至多等于4．假设可以等于5，则不妨先取出其中4个点，为，，，，则构成一个正四面体的四个顶点，设第5个点为点，则点和点，，也要构成一个正四面体，此时点要么跟点重合，要么点和点关于平面对称，但此时的长又不等于，故矛盾．故选B．‎