专题38 空间几何体的结构、三视图和直观图-2020年领军高考数学一轮复习（文理通用） Word版含解析 33页

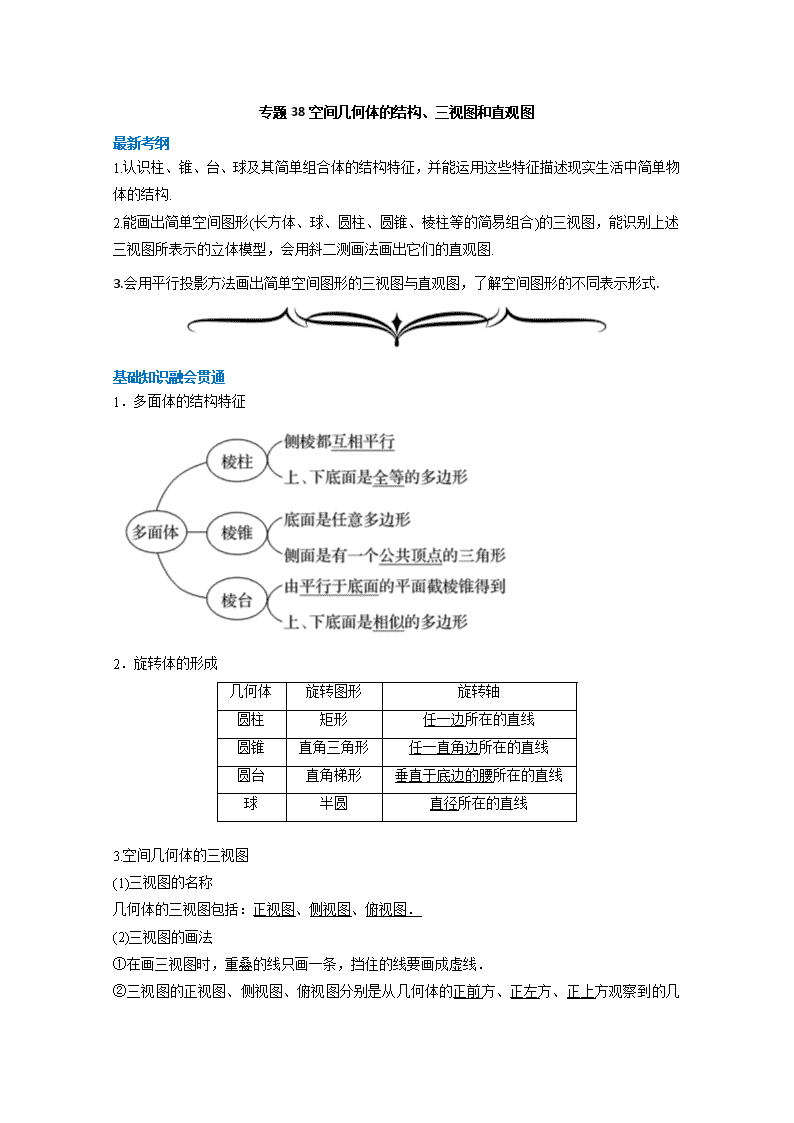
专题38空间几何体的结构、三视图和直观图 最新考纲 ‎1.认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构.‎ ‎2.能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图，能识别上述三视图所表示的立体模型，会用斜二测画法画出它们的直观图.‎ ‎3.会用平行投影方法画出简单空间图形的三视图与直观图，了解空间图形的不同表示形式.‎ 基础知识融会贯通 ‎1．多面体的结构特征 ‎2．旋转体的形成 几何体 旋转图形 旋转轴 圆柱 矩形 任一边所在的直线 圆锥 直角三角形 任一直角边所在的直线 圆台 直角梯形 垂直于底边的腰所在的直线 球 半圆 直径所在的直线 ‎3.空间几何体的三视图 ‎(1)三视图的名称 几何体的三视图包括：正视图、侧视图、俯视图．‎ ‎(2)三视图的画法 ‎①在画三视图时，重叠的线只画一条，挡住的线要画成虚线．‎ ‎②三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上 方观察到的几何体的正投影图．‎ ‎4．空间几何体的直观图 空间几何体的直观图常用斜二测画法来画，其规则是 ‎(1)原图形中x轴、y轴、z轴两两垂直，直观图中，x′轴，y′轴的夹角为45°或135°，z′轴与x′轴和y′轴所在平面垂直．‎ ‎(2)原图形中平行于坐标轴的线段，直观图中仍平行于坐标轴；平行于x轴和z轴的线段在直观图中保持原长度不变；平行于y轴的线段在直观图中长度变为原来的一半．‎ ‎【知识拓展】‎ ‎1．常见旋转体的三视图 ‎(1)球的三视图都是半径相等的圆．‎ ‎(2)水平放置的圆锥的正视图和侧视图均为全等的等腰三角形．‎ ‎(3)水平放置的圆台的正视图和侧视图均为全等的等腰梯形．‎ ‎(4)水平放置的圆柱的正视图和侧视图均为全等的矩形．‎ ‎2．斜二测画法中的“三变”与“三不变”‎ ‎“三变” ‎“三不变” 重点难点突破 ‎【题型一】空间几何体的结构特征 ‎【典型例题】‎ 有下列四个命题：‎ ‎①三个点可以确定一个平面；‎ ‎②圆锥的侧面展开图可以是一个圆面；‎ ‎③底面是等边三角形，三个侧面都是等腰三角形的三棱锥是正三棱锥；‎ ‎④过球面上任意两不同点的大圆有且只有一个．‎ 其中正确命题的个数是（　　）‎ A．0 B．1 C．2 D．3‎ ‎【解答】解：当三点共线时，不能确定平面，故①错误；‎ 由圆锥的母线一定比底面半径大，可得圆锥的侧面展开图是一个圆心角不超过2π的扇形，故②错误；‎ 底面是等边三角形，三个侧面都是等腰三角形的三棱锥不一定是正三棱锥，故③错误；‎ 如果两点是球的两个极点，则过两点的大圆有无数个，故④错误 故选：A． 【再练一题】‎ 正三棱柱ABC﹣A1B1C1中，所有棱长均为2，点E，F分别为棱BB1，A1C1的中点，若过点A，E，F作一截面，则截面的周长为（　　）‎ A．2+2 B． C． D．‎ ‎【解答】‎ 解：如图将三棱柱三棱柱ABC﹣A1B1C1扩大为如图的正三棱柱，‎ 其中AA''＝2AA1＝4，AH＝2AB＝4，‎ 则点E为AH'的中点，点F为AC''的中点．设H'F∩B1C1＝I，‎ 所以EF∥H'C''，‎ 所以过点A，E，F的截面为AEIF，‎ 因为△ABE和△AA1F均为两直角边分别为2，1的直角三角形，‎ ‎∴AE＝AF，‎ 在事件A1H'D'中，如图：‎ 连接HF，交B1C1于I，连接H'C1，‎ 则I为三角形A1H'C1的重心，‎ 所以B1I，FI，‎ 因为H'C1＝4×sin60°＝2，C1F＝1，所以FI．‎ 又因为B1E⊥平面A1B1C1，‎ 所以三角形EB1I为直角三角形，且EB1＝1，B1I，所以EI，‎ 所以，截面的周长为：2．‎ 故选：B．‎ ‎ 思维升华 (1)关于空间几何体的结构特征辨析关键是紧扣各种空间几何体的概念，要善于通过举反例对概念进行辨析，即要说明一个命题是错误的，只需举一反例即可．‎ ‎(2)圆柱、圆锥、圆台的有关元素都集中在轴截面上，解题时要注意用好轴截面中各元素的关系．‎ ‎(3)既然棱(圆)台是由棱(圆)锥定义的，所以在解决棱(圆)台问题时，要注意“还台为锥”的解题策略．‎ ‎【题型二】简单几何体的三视图 命题点1　已知几何体，识别三视图 ‎【典型例题】‎ 正方体被切去一个角后得到的几何体如图所示，其侧视图（由左往右看）是（　　）‎ A． B． C． D．‎ ‎【解答】解：根据几何体，转换为三视图，‎ 所以平面图形的侧视图为：‎ 故选：A． 【再练一题】‎ 已知棱长都为2的正三棱柱ABC﹣A1B1C1的直观图如图，若正三棱柱ABC﹣A1B1C1绕着它的一条侧棱所在直线旋转，则它的侧视图可以为（　　）‎ A． B． ‎ C． D．‎ ‎【解答】解：四个选项高都是2，‎ 若侧视图为A，中间应该有一条竖直的实线或虚线．‎ 若为C，则其中有两条侧棱重合，不应有中间竖线．‎ 若为D，则长应为，而不是1．‎ 故选：B． 命题点2　已知三视图，判断几何体的形状 ‎【典型例题】‎ 已知如图是一个几何体的三视图及有关数据如图所示，则该几何体的棱的长度中，最大的是（　　）‎ A． B． C． D．‎ ‎【解答】解：几何体可以看作长方体的一部分，‎ 也可以看作是正三棱柱去掉一个三棱锥的几何体，如图所示；‎ 则该几何体的棱长为：AE＝AD＝2，‎ AC＝BC＝BE＝ED＝DC＝AC＝BC＝2．‎ 所以该几何体的棱长最大的是2．‎ 故选：B． 【再练一题】‎ 一个几何体的三视图如图所示，该几何体表面上的点P在正视图上的对应点为P，点A、B、C在俯视图上的对应点为A、B、C，则PA与BC所成角的余弦值为（　　）‎ A． B． C． D．‎ ‎【解答】解：由三视图知，该几何体是直四棱锥P﹣ABCD，且PD⊥平面ABCD，如图所示；‎ 取CD的中点M，连接AM、PM，则AM∥BC，∴∠PAM是异面直线PA与BC所成的角，‎ ‎△PAM中，PA＝2，AM＝PM，‎ ‎∴cos∠PAM，‎ 即PA与BC所成角的余弦值为．‎ 故选：B． .‎ 命题点3　已知三视图中的两个视图，判断第三个视图 ‎【典型例题】‎ 一个锥体的主视图和左视图如图所示，下面选项中，不可能是该锥体的俯视图的是（　　）‎ A． B． ‎ C． D．‎ ‎【解答】解：本题中给出了正视图与左视图，故可以根据正视图与俯视图长对正，左视图与俯视图宽相等来找出正确选项 A中的视图满足三视图的作法规则；‎ B中的视图满足三视图的作法规则；‎ C中的视图不满足三视图的作法规则中的宽相等，故其为错误选项；‎ D中的视图满足三视图的作法规则；‎ 故选：C． 【再练一题】‎ 如图是某三棱锥的正视图与俯视图，已知网格纸上小正方形的边长为a，则该三棱锥的侧视图可能为（　　）‎ A． B． C． D．‎ ‎【解答】解：根据三棱锥的正视图和俯视图，转换为几何体为：‎ 根据三视图的棱长，‎ 得到：该几何体的侧视图为，有一条棱垂直于下底面，一条棱为虚线，‎ 故选：C． 思维升华 三视图问题的常见类型及解题策略 ‎(1)由几何体的直观图求三视图．注意观察方向，注意看到的部分用实线表示，不能看到的部分用虚线表示．‎ ‎(2)由几何体的三视图还原几何体的形状．要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为实物图．‎ ‎(3)由几何体的部分视图画出剩余的部分视图．先根据已知的一部分三视图，还原、推测直观图的可能形状，然后再找其剩下部分三视图的可能形状．当然作为选择题，也可将选项逐项代入，再看看给出的部分三视图是否符合．‎ ‎【题型三】空间几何体的直观图 ‎【典型例题】‎ 已知一个三棱锥的高为3，其底面用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形（如右图所示），则此三棱锥的体积为（　　）‎ A． B． C． D．2‎ ‎【解答】解：∵斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形，‎ ‎∴三棱锥的底面积为，‎ ‎∵三棱锥的高为3，‎ ‎∴三棱锥的体积为：，‎ 故选：A． 【再练一题】‎ 一个几何体的三视图如图所示，则这个几何体的直观图为（　　）‎ A． B． ‎ C． D．‎ ‎【解答】解：由已知的三视图可得：该几何体是一个以俯视图为底面的四棱锥，而且有一侧棱垂直与底面，结合俯视图，可知B满足，‎ 故选：B． 思维升华 用斜二测画法画直观图的技巧 在原图形中与x轴或y轴平行的线段在直观图中与x′轴或y′轴平行，原图中不与坐标轴平行的直线段可以先画出线段的端点再连线，原图中的曲线段可以通过取一些关键点，作出在直观图中的相应点后，用平滑的曲线连接而画出．‎ 基础知识训练 ‎1．【福建省宁德市部分一级达标中学2018-2019学年高一下学期期中考试】一个圆锥的表面积为，它的侧面展开图是圆心角为的扇形，该圆锥的母线长为（ ）‎ A． B．4 C． D．‎ ‎【答案】B ‎【解析】‎ 设圆锥的底面半径为，母线长为 它的侧面展开图是圆心角为的扇形 ‎ 又圆锥的表面积为 ，解得：‎ 母线长为：‎ 本题正确选项：‎ ‎2．【重庆市第一中学2018-2019学年高一下学期期中考试】下列命题正确的是（ ）‎ A．有两个面平行，其余各面都是四边形的几何体叫棱柱。‎ B．有两个面平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行的几何体叫棱柱。‎ C．绕直角三角形的一边旋转所形成的几何体叫圆锥。‎ D．用一个面去截棱锥，底面与截面之间的部分组成的几何体叫棱台。‎ ‎【答案】B ‎【解析】‎ 对于A选项，几何体可以是棱台，满足有两个面平行，其余各面都是四边形，故选项不正确；对于B，根据课本中棱柱的概念得到是正确的；对于C，当绕直角三角形的斜边旋转时构成的几何体不是圆锥，故不正确；对于D，用平行于底面的平面截圆锥得到的剩余的几何体是棱台，故不正确.‎ 故答案为：B.‎ ‎3．【江西省南昌八中、二十三中、十三中2018-2019学年下学期高二期中考试】以下命题中真命题的序号是（　　）‎ ‎①若棱柱被一平面所截，则分成的两部分不一定是棱柱；‎ ‎②有两个面平行，其余各面都是平行四边形的几何体叫棱柱；‎ ‎③有一个面是多边形，其余各面都是三角形的多面体一定是棱锥；‎ ‎④当球心到平面的距离小于球面半径时，球面与平面的交线总是一个圆．‎ A．①④ B．②③④ C．①②③ D．①②③④‎ ‎【答案】A ‎【解析】‎ ‎①若棱柱被一平面所截，则分成的两部分不一定是棱柱，只有平行于底面的平面截棱柱分成的两部分一定是棱柱，正确.‎ ‎②有两个面平行，其余各面都是平行四边形的几何体并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱，故不正确；‎ ‎③有一个面是多边形，其余各面都是三角形的多面体不一定是棱锥，由三棱锥的定义可知：其余各面都是共有同一个顶点的三角形的多面体，故不正确；‎ ‎④当球心到平面的距离小于球面半径时，球面与平面的交线总是一个圆，正确．‎ 综上可得：只有①④正确．‎ 故选：A．‎ ‎4．【浙江省嘉兴市2018-2019学年高二下学期期末】已知某几何体的三视图如图所示，则该几何体的体积为 A． B． C． D．‎ ‎【答案】A ‎【解析】‎ 由三视图可知，几何体为三棱锥 三棱锥体积为：‎ 本题正确选项：‎ ‎5．【天津市和平区第一中学2018-2019学年高一下学期期中】一个圆锥 的高和底面直径相等，且这个圆锥和圆柱的底面半径及体积也都相等，则圆锥和圆柱的侧面积的比值为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】‎ 不妨设圆锥的底面半径为，高为，设圆柱的底面半径，高为.根据圆锥和圆柱的底面半径及体积也都相等.得，记得.圆锥的母线长为，故两者侧面积比为，故选C.‎ ‎6．【辽宁省葫芦岛市普通高中2019届高三第二次模拟考试】某几何体的三视图如图所示，则该几何体的表面积（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】‎ 由三视图可知，该几何体为两个半圆柱构成，其表面积为，故选D.‎ ‎7．【河南省八市重点高中联盟“领军考试”2019届高三第五次测评】如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的各个面中是直角三角形的个数为（ ）‎ A．1 B．2 C．3 D．4‎ ‎【答案】C ‎【解析】‎ 三视图还原为如图所示三棱锥A-BCD：‎ 由正方体的性质得 为直角三角形， 为正三角形 故选：C ‎8．【广东省东莞市2019届高三第二学期高考冲刺试题（最后一卷)】如图画出的是某几何体的三视图，网格纸上小正方形的边长为1，则该几何体的体积为（ ）‎ A． B．‎ C． D．‎ ‎【答案】A ‎【解析】‎ 由三视图还原原几何体，如图所示，可知原几何体为组合体，是半径为2的球的与半径为的球的，‎ 其球的组合体的体积 .‎ 故选：A．‎ ‎9．【山东省淄博市部分学校2019届高三5月阶段性检测（三模)】某几何体的三视图如图所示，则该几何体的表面积为（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】‎ 由已知中的三视图可得该几何体是一个以俯视图为底面的四分之三圆柱，‎ 其底面半径为1，高为2，‎ 故其表面积：，‎ 故选：．‎ ‎10．【2019年山西省太原市高三模拟试题（二)】下图是某几何体的三视图，其中网格纸上小正方形的边长为1，则该几何体的体积为（ ）‎ A． B． C．4 D．‎ ‎【答案】C ‎【解析】‎ 画出三视图对应的几何体如下图所示三棱锥，根据三棱锥体积计算公式得所求体积为，故选C.‎ ‎11．【2015-2016学年河北省冀州市中学高一下开学考试】正方体中，分别是的中点．那么，正方体的过的截面图形是（ ）‎ A．三角形 B．四边形 C．五边形 D．六边形 ‎【答案】D ‎【解析】‎ 延长QP，CB交于V，连接RV，交BB1于S．‎ 作RT∥PQ，交C1D1于M．延长PQ，CD交于T，连接TM，交DD1于N．‎ 如图所示：‎ 正方体过P、Q、R的截面图形是六边形，‎ 且是边长是正方体棱长的倍的正六边形．‎ 故答案为：D ‎12．【上海市虹口区2018-2019学年高二下学期数学期中统考】在棱长为a的正方体ABCD﹣A1B1C1D1中，M、N、P分别是正方形ABCD、正方形BB1C1C和正方形ABB1A1的中心，则过点M、N、P的平面截正方体的截面面积为_____．‎ ‎【答案】‎ ‎【解析】‎ 依题意，M、N、P分别是正方形ABCD、正方形BB1C1C和正方形ABB1A1的中心，即M，N，P分别为AB1、B1C、AC的中点，所以过点M、N、P的平面截正方体的截面为三角形AB1C，如图．‎ 因为正方体的棱长为a，所以三角形AB1C的边长为，所以三角形AB1C，的面积为：‎ S＝ ．‎ 故答案为：‎ ‎13．【山东省德州市2019届高三第二次练习】如图．网络纸上小正方形的边长为1．粗实线画出的是某几何体的三视图，则该几何体的体积为______．‎ ‎【答案】‎ ‎【解析】‎ 根据三视图知，该几何体是三棱柱与半圆锥的组合体，如图所示；‎ 结合图中数据，计算它的体积为 ‎．‎ 故答案为：．‎ ‎14．【山东省聊城市2019届高三三模】如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体外接球的表面积为__________．‎ ‎【答案】‎ ‎【解析】‎ 由题得几何体原图如图所示，底面等腰三角形的腰长为，‎ 由余弦定理得，‎ 所以,‎ 在△ADC中，AC=1,，‎ 所以,‎ 所以几何体外接球的半径为，‎ 所以几何体外接球的表面积为.‎ 故答案为：‎ ‎15．【天津市和平区2019届高三一模】已知一个几何体的三视图如图所示（单位：），则该几何体的体积为_________.‎ ‎【答案】‎ ‎【解析】‎ 由三视图可知，题中所给的几何体是由一个长方体挖去一个圆锥形成的组合体，‎ 其中长方体的长宽高分别为，‎ 圆锥的底面半径为，圆锥的高，‎ 故所求几何体的体积.‎ ‎16．【安徽省蚌埠市2019届高三年级第三次教学质量检查考试】已知球的半径为3，圆与圆为该球的两个小圆，半径相等且所在平面互相垂直，圆与圆的公共弦的长为，点是弦的中点，则四边形的面积为__________．‎ ‎【答案】2‎ ‎【解析】‎ 圆与圆为该球的两个小圆半径相等,且所在平面互相垂直，‎ 可得四边形OABC为正方形，设正方形的边长为x,小圆的半径为r,‎ 在中可得，在中可得，即 解得，故四边形的面积为，‎ 故答案为：2‎ ‎17．【湖北省荆州市沙市中学2018-2019学年高一5月月考】在如图所示的三棱锥A-BCD中，BD=2，DC=3，∠DAB+∠BAC+∠DAC=90°，∠ADB=∠BDC=∠ADC=90°．现有一只蚂蚁从点D出发经三棱锥A-BCD的三个侧面绕行一周后回到点D，则蚂蚁爬行的最短距离为_______．‎ ‎【答案】‎ ‎【解析】‎ 三棱锥的侧面展开图如下图（实线部分）所示：‎ 由题意可知，蚂蚁爬行的最短距离即为：‎ ‎ ‎ 且 四边形为正方形 设，则，‎ ‎ ，解得：‎ ‎ ‎ 本题正确结果：‎ ‎18．【上海市金山中学2018-2019学年高二5月月考】棱长为1的正方体中，点、分别在线段、上运动（不包括线段端点），且.以下结论：①；②若点、分别为线段、的中点，则由线与确定的平面在正方体上的截面为等边三角形；③四面体的体积的最大值为；④直线与直线的夹角为定值.其中正确的结论为______.（填序号）‎ ‎【答案】① ② ③‎ ‎【解析】‎ ‎①作NE⊥BC，MF⊥AB，垂足分别为E，F，∵AM＝BN，∴NE＝MF，∴四边形MNEF是矩形，∴MN∥FE，∵AA1⊥面AC，EF⊂面AC，∴AA1⊥EF，∴AA1⊥MN，故①正确；‎ ‎②点M、N分别为线段AB1、BC1的中点，则由线MN与AB1确定的平面在正方体ABCD﹣A1B1C1D1 上的截面为△AB1C，为等边三角形，故②正确．‎ ‎③设，则＝dM﹣BCN，又AM=BN=,‎ ‎∴=，dM﹣BCN =，∴＝dM﹣BCN=，当且仅当时取得最大值，故③成立；‎ ‎④设，当接近于0时，直线与直线的夹角近似于直线和直线的夹角，接近于，当接近于1时，直线与直线的夹角近似于直线和直线 的夹角，接近于，故④不正确；‎ 综上可知，正确的结论为①②③‎ 故答案为：①②③‎ ‎19．【四川省绵阳市2019届高三第三次诊断性考试】在《九章算术》中有称为“羡除”的五面体体积的求法．现有一个类似于“羡除”的有三条棱互相平行的五面体，其三视图如图所示，财该五面体的体积为______．‎ ‎【答案】24.‎ ‎【解析】‎ 由三视图可得，该几何体为如下图所示的五面体，‎ 其中，底面为直角三角形，且，侧棱与底面垂直，且．‎ 过点作，交分别于，‎ 则棱柱为直棱柱，四棱锥的底面为矩形，高为．‎ 所以．‎ 故答案为：．‎ ‎20．【2019年辽宁省大连市高三5月双基考试】如图，在小正方形边长为1的网格中画出了某多面体的三视图，则该多面体的外接球表面积为______．‎ ‎【答案】34π ‎【解析】‎ 由三视图知，该几何体中一个侧面SAC与底面ABC垂直，‎ 由三视图的数据可得OA＝OC＝2，OB＝OS＝4，‎ 建立空间直角坐标系O﹣xyz，如图所示；‎ 则A（0，﹣2，0），B（4，0，0），C（0，2，0），S（0，0，4），‎ 则三棱锥外接球的球心I在平面xOz上，设I（x，0，z）；‎ 由得，‎ ‎，‎ 解得x＝z；‎ ‎∴外接球的半径R＝|BI|，‎ ‎∴该几何体外接球的表面积为 S＝4πR2＝4π34π．‎ 故答案为：34π．‎ 能力提升训练 ‎1．【山东省栖霞市2019届高三高考模拟卷（新课标I)】某几何体的三视图如图所示，则该几何体的表面积为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】‎ 由三视图可知几何体为一个正方体和一个圆锥的组合体 则该几何体的表面积为：正方体的表面积与圆锥侧面积之和 正方体的表面积：‎ 圆锥的侧面积：‎ 几何体的表面积：‎ 本题正确选项：‎ ‎2．‎ ‎【河北省石家庄市2019届高三毕业班模拟考试一A卷】如图，某几何体的三视图都是边长为的正方形，则该几何体的体积为（）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】‎ 如图所示，在棱长为1的正方体中，‎ 三视图所对的几何体为该正方体去掉三棱锥和三棱锥所得的组合体，‎ 其体积为：.‎ 本题选择D选项.‎ ‎3．【四川省成都市第七中学2019届高三二诊模拟考试】某多面体的三视图如图所示，则该几何体的体积与其外接球的体积之比为（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】‎ 几何体为如图三棱锥S-ABC，SA=2,SC=4,BD=2,体积为，其外接球球心为SB中点,外接球半径为，‎ 所以几何体的体积与其外接球的体积之比为，选A.‎ ‎4．【福建省漳州市2018-2019学年高三毕业班第一次教学质量检查测试】如图，网格纸的小正方形的边长是1，在其上用粗实线和粗虚线画出了某几何体的三视图，则该几何体的体积是（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】‎ 根据空间结构体的三视图，得原空间结构体如下图所示：‎ 该几何体是由下面半球的和上面四棱锥的组成 由三视图的棱长及半径关系，可得几何体的体积为 ‎ ‎ 所以选A ‎5．‎ ‎【江西省新余四中、上高二中2019届高三第二次联考】一个几何体的三视图如图所示,该几何体的体积为( )‎ A． B． C． D．‎ ‎【答案】A ‎【解析】‎ 根据几何体的三视图得该几何体是四棱锥M-PSQN且四棱锥是棱长为2的正方体的一部分,直观图如图所示,由正方体的性质得,所以该四棱锥的体积为:‎ ‎ ,故A正确.‎ ‎6．【江西省新八校2019届高三第二次联考】已知一个四棱锥的正(主)视图和俯视图如图所示，其中a+b=10.则该四棱锥的高的最大值为_____‎ ‎【答案】‎ ‎【解析】‎ 解：如图所示，‎ 由题意知，平面平面，设点到AD的距离为，‎ 当最大时，四棱锥的高最大，‎ 因为，‎ 所以点的轨迹为一个椭圆，‎ 由椭圆的性质得，当时，取得最大值，‎ 即该四棱锥的高的最大值为.‎ ‎7．【湖南省岳阳市第一中学2019届高三第一次模拟（5月)】某三棱锥的三视图如图所示，正视图与侧视图是两个全等的等腰直角三角形，直角边长为1，俯视图为正方形，则该三棱锥的体积为______.‎ ‎【答案】‎ ‎【解析】‎ 设三棱锥为P﹣ABC，O为P在底面上的射影，‎ 由三视图可知ABCO为边长为1的正方形，且棱锥的高PO＝1，‎ ‎∴三棱锥的体积．‎ 故答案为：．‎ ‎8．【北京市朝阳区2019届高三第二次（5月)综合练习（二模)】某几何体的三视图如图所示，则该几何体的体积为______.‎ ‎【答案】‎ ‎【解析】‎ 由三视图可知，该几何体由上部四棱柱、下部圆柱组成的组合体，‎ 四棱柱的底面为边长为3的正方形，高为1，故体积为：，‎ 圆柱的底面圆直径为1，高为2，故体积为：，‎ 所求体积为，‎ 故答案为：‎ ‎9．【河南省六市2019届高三第二次联考】我国古代数学名著《九章算术》中有如下 问题：“今有羡除，下广六尺，上广一丈，深三尺，末广八尺，无深，袤七尺。问积几何”，羡除是一个五面体，其中三个面是梯形，另两个面是三角形，已知一个羡除的三视图如图粗线所示，其中小正方形网格的边长为1，则该羡除的体积为__________．‎ ‎【答案】24‎ ‎【解析】‎ 如图所示，在长宽高分别为的长方体中，，，‎ 三视图所对应的几何体是多面体，‎ 该组合体是由一个三棱锥和一个四棱锥组成的组合体，其体积：‎ ‎.‎ 故答案为：．‎ ‎10．【安徽省芜湖市2019届高三模拟考试】某空间几何体的三视图如图所示，其中俯视图的虚线为半圆弧，则该几何体的体积为________.‎ ‎【答案】‎ ‎【解析】‎ 由题意可知几何体是一个底面边长为4的四棱锥 挖去一个底面半径为2的半圆锥，如图：‎ 几何体的体积为：‎ 故答案为 ‎ ‎