2020届江苏省高考数学二轮复习综合仿练（一） 6页

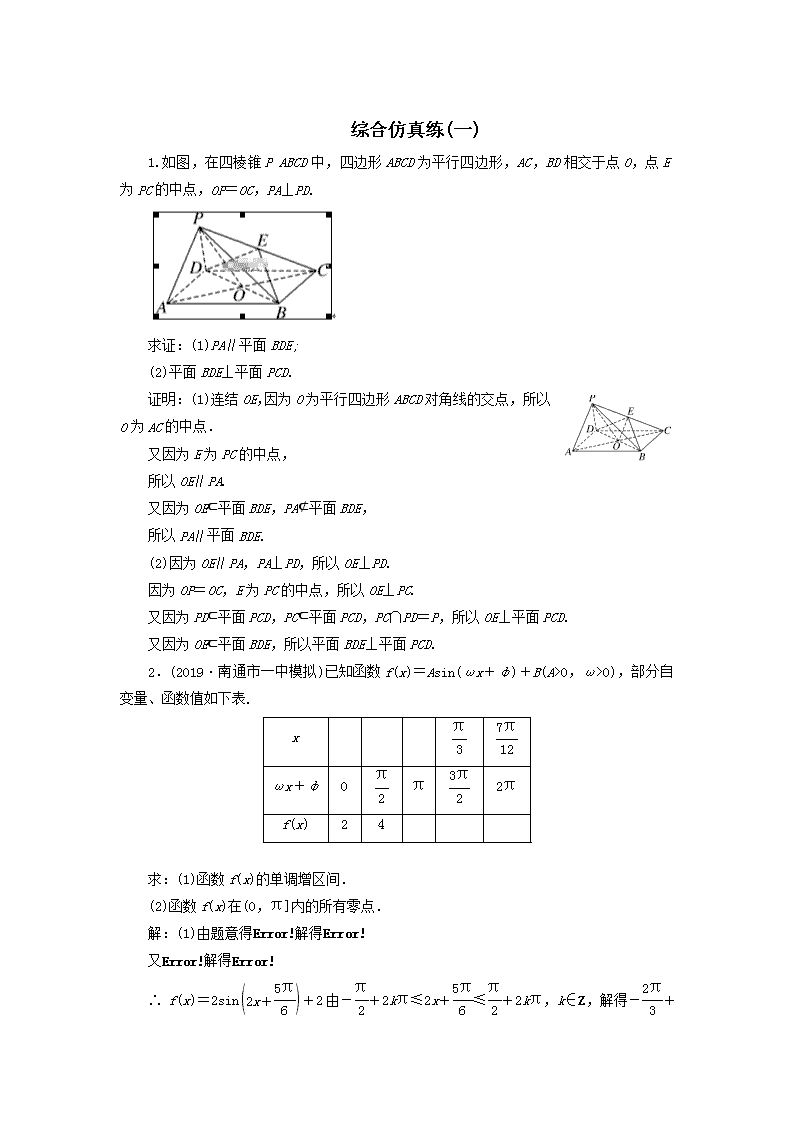
综合仿真练(一)‎ ‎1.如图，在四棱锥PABCD中，四边形ABCD为平行四边形，AC，BD相交于点O，点E为PC的中点，OP＝OC，PA⊥PD.‎ 求证：(1)PA∥平面BDE; ‎ ‎(2)平面BDE⊥平面PCD.‎ 证明：(1)连结OE，因为O为平行四边形ABCD对角线的交点，所以O为AC的中点．‎ 又因为E为PC的中点，‎ 所以OE∥PA. ‎ 又因为OE⊂平面BDE，PA⊄平面BDE，‎ 所以PA∥平面BDE. ‎ ‎(2)因为OE∥PA，PA⊥PD，所以OE⊥PD. ‎ 因为OP＝OC，E为PC的中点，所以OE⊥PC. ‎ 又因为PD⊂平面PCD，PC⊂平面PCD，PC∩PD＝P，所以OE⊥平面PCD. ‎ 又因为OE⊂平面BDE，所以平面BDE⊥平面PCD.‎ ‎2．(2019·南通市一中模拟)已知函数f(x)＝Asin(ωx＋φ)＋B(A>0，ω>0)，部分自变量、函数值如下表.‎ x ωx＋φ ‎0‎ π ‎2π f(x)‎ ‎2‎ ‎4‎ 求：(1)函数f(x)的单调增区间．‎ ‎(2)函数f(x)在(0，π]内的所有零点．‎ 解：(1)由题意得解得 ‎ 又解得 ‎ ‎∴ f(x)＝2sin＋2由－＋2kπ≤2x＋≤＋2kπ，k∈Z，解得－＋kπ≤x ‎≤－＋kπ，k∈Z，‎ ‎∴函数f(x)单调增区间为 (k∈Z)．‎ ‎(2)∵f(x)＝2sin＋2＝0，‎ ‎∴sin＝－1.‎ ‎∵x∈(0，π]，∴<2x＋≤2π＋，∴2x＋＝，解得：x＝.‎ ‎∴函数f(x)在(0，π]内的零点为.‎ ‎3．(2019·扬州四模)已知椭圆C：＋＝1(a>b>0)的离心率为，左顶点为A，右焦点为F，且AF＝5. ‎ ‎(1)求椭圆C的方程；‎ ‎(2)已知圆M的圆心M，半径为r，点P为椭圆上的一点，若圆M与直线PA，PF都相切，求此时圆M的半径r.‎ 解：(1)∵椭圆离心率为，左顶点为A，右焦点为F，且AF＝5.‎ ‎∴解得∴b2＝15，∴椭圆C的方程为：＋＝1.‎ ‎(2)由题意得：A(－4,0)，F(1,0)，设点P的坐标为(x0，y0)，则＋＝1‎ ‎①当x0＝1时，直线PF：x＝1，与圆M相切，则R＝1－＝，‎ 不妨取P，直线PA：y＝(x＋4)，即3x－4y＋12＝0，‎ ‎∴点M到直线PF的距离为＝＝r ∴直线PF与圆M相切 ‎∴当r＝时，圆M与直线PA，PF都相切．‎ ‎②当x0＝－4时，点P与点A重合，不符合题意；‎ ‎③当x0≠1且x0≠－4时，直线PA：y＝(x＋4)，PF：y＝(x－1)‎ 化简得：PA：y0x－(x0＋4)y＋4y0＝0，‎ PF：y0x－(x0－1)y－y0＝0‎ ‎∵圆M与直线PA，PF都相切 ‎ ‎∴＝＝r ‎∵y0≠0，又y＝15代入化简得：x－122x0＋121＝0，解得：x0＝1或x0＝121‎ ‎∵－40), ‎ 当a≤3时，f′(x)＜0，f(x)在(0，＋∞)上单调递减； ‎ 当a＞3时，由f′(x)＜0，得0＜x＜，‎ f(x)在0，上单调递减，‎ 由f′(x)＞0，得x＞，f(x)在上单调递增. ‎ 因为函数f(x)在(1，＋∞)上为单调增函数，‎ 所以a＞3且≤1，所以a≥5, ‎ 所以实数a的最小值为5. ‎ 法二：因为函数f(x)在(1，＋∞)上为单调增函数，‎ 所以f′(x)＝a－3－≥0在(1，＋∞)上恒成立， ‎ 所以a≥3＋在(1，＋∞)上恒成立， ‎ 又当x＞1时，3＋＜5, 所以a≥5，‎ 所以实数a的最小值为5. ‎ ‎(2)令g(x)＝f(x)＋3x＝a(x－1)－2ln x，x∈(0,1]，‎ 所以g′(x)＝a－. ‎ ‎①当a≤2时，由于x∈(0,1]，所以≥2，‎ 所以g′(x)≤0，g(x)在(0,1]上单调递减，‎ 所以g(x)min＝g(1)＝0，所以对任意x∈(0,1]，g(x)≥g(1)＝0，即对任意x∈(0,1]不等式f(x)＋3x≥0都成立，所以a≤2; ‎ ‎②当a＞2时，由g′(x)＜0，得0＜x＜，g(x)在上单调递减；‎ 由g′(x)＞0，得x＞，g(x)在上单调递增．‎ 所以，存在∈(0,1)，使得g＜g(1)＝0，不合题意．‎ 综上所述，实数a的取值范围为(－∞，2]．‎ ‎6．已知数列{an}的前n项和为Sn，且Sn＝2an－1.‎ ‎(1)求数列{an}的通项公式；‎ ‎(2)记集合M＝{n|n(n＋1)≥λan，n∈N*}，若M中有3个元素，求λ的取值范围；‎ ‎(3)是否存在等差数列{bn}，使得a1bn＋a2bn－1＋a3bn－2＋…＋anb1＝2n＋1－n－2对一切n∈N*都成立？若存在，求出bn；若不存在，说明理由．‎ 解：(1)当n＝1时，S1＝2a1－1，得a1＝1.‎ 当n≥2时，由Sn＝2an－1，①‎ 得Sn－1＝2an－1－1，②‎ ‎①－②，得an＝2an－1，即＝2(n≥2)．‎ 因此{an}是首项为1，公比为2的等比数列，所以an＝2n－1. ‎ ‎(2)由已知可得λ≤，令f(n)＝，‎ 则f(1)＝2，f(2)＝3，f(3)＝3，f(4)＝，f(5)＝， ‎ 下面研究f(n)＝的单调性，‎ 因为f(n＋1)－f(n)＝－＝，‎ 所以，当n≥3时，f(n＋1)－f(n)＜0，f(n＋1)＜f(n)，‎ 即f(n)单调递减. ‎ 因为M中有3个元素，所以不等式λ≤解的个数为3，所以2＜λ≤，即λ的取值范围为.‎ ‎(3)设存在等差数列{bn}使得条件成立，‎ 则当n＝1时，有a1b1＝22－1－2＝1，所以b1＝1.‎ 当n＝2时，有a1b2＋a2b1＝23－2－2＝4，所以b2＝2.‎ 所以等差数列{bn}的公差d＝1，所以bn＝n. ‎ 设S＝a1bn＋a2bn－1＋a3bn－2＋…＋anb1，‎ S＝1·n＋2(n－1)＋22(n－2)＋…＋2n－2·2＋2n－1·1，③‎ 所以2S＝2·n＋22(n－1)＋23(n－2)＋…＋2n－1·2＋2n·1，④‎ ‎④－③，得S＝－n＋2＋22＋23＋…＋2n－1＋2n ＝－n＋＝2n＋1－n－2，‎ 所以存在等差数列{bn}，‎ 且bn＝n满足题意．‎