浙江省2019学年第二学期“山水联盟”高考模拟考数学试卷 13页

‎ ‎ ‎2019学年第二学期“山水联盟”高考模拟考试 数学学科试题 命题：浙鳌中学高三数学组 审校：淳安中学余建明 审核：淳安中学叶祝明 考生须知：‎ ‎1．本试题卷分选择题和非选择题两部分，满分150分．考试用时120分钟；‎ ‎2．答题前，在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字；‎ ‎3．所有答案必须写在答题卷上，写在试卷上无效；‎ ‎4．考试结束后，只需上交答题卷．‎ 参考公式：‎ 若事件A，B互斥，则 若事件A，B相互独立，则P（AB）= P（A）P（B）‎ 若事件A在一次试验中发生的概率是p，则n次独立重复试验中事件A恰好发生k次的概率 台体的体积公式 其中，分别表示台体的上、下底面积，h表示台体的高 柱体的体积公式 其中S表示柱体的底面积，h表示柱体的高 锥体的体积公式 其中S表示锥体的底面积，h表示锥体的高 球的表面积公式：，球的体积公式：‎ 其中R表示球的半径 选择题部分（共40分）‎ 一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知集合，，则（ ）‎ ‎ ‎ A． B．‎ C． D．‎ ‎2．已知双曲线，其虚轴长为2，则双曲线的离心率是（ ）‎ A． B． C．3 D．‎ ‎3．若实数x，y满足约束条件，则的最大值是（ ）‎ A．3 B．-2 C．-3 D．1‎ ‎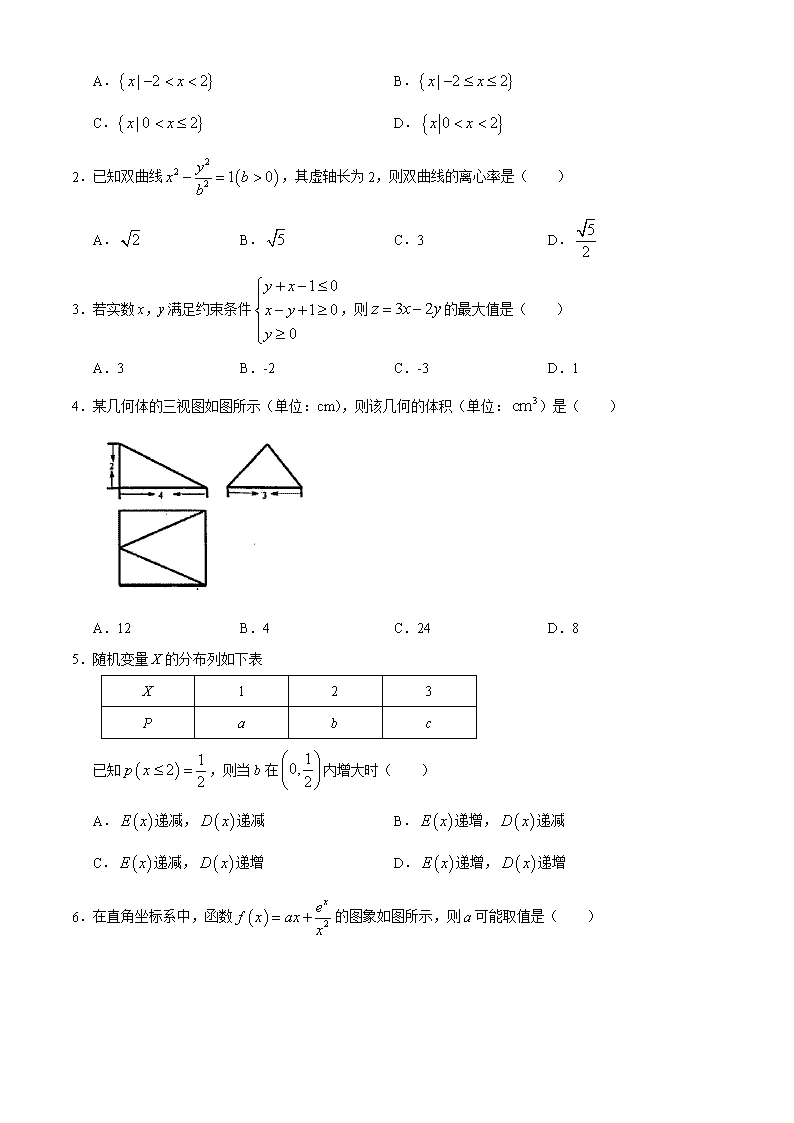4．某几何体的三视图如图所示（单位：cm），则该几何的体积（单位：）是（ ）‎ A．12 B．4 C．24 D．8‎ ‎5．随机变量X的分布列如下表 X ‎1‎ ‎2‎ ‎3‎ P a b c 已知，则当b在内增大时（ ）‎ A．递减，递减 B．递增，递减 C．递减，递增 D．递增，递增 ‎6．在直角坐标系中，函数的图象如图所示，则a可能取值是（ ）‎ ‎ ‎ A． B． C．1 D．0‎ ‎7．设A、B、C三点不共线，则“与的夹角是钝角”是“”的（ ）‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎8．已知正方体，P是平面上的动点，M是线段BC的中点，满足PM与所成的角为，则动点P的轨迹为（ ）‎ A．圆 B．椭圆 C．双曲线 D．抛物线 ‎9．已知在内存在零点，则实数a的取值范围（ ）‎ A． B． C． D．‎ ‎10．已知数列满足，则下列错误的是（ ）‎ A．若时，则数列单调递增 B．存在时，使数列为常数列 C．若时，则单调递减数列 D．若时，则 非选择题部分（共110分）‎ 二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分．‎ ‎11．《数书九章》卷五中第二题，原文如下：问有沙田一段，有三斜，其小斜一十二里，中斜一十四里，大斜一十五里．里法三百步，欲知为田几何？答曰：田积三百一十五顷．术曰：以少广求之，以小斜幂 ‎ ‎ ‎（）并大斜幂（）,减中斜幂（），并半之，自乘于上；以小斜幂乘大斜幂，减上，以四约之，为实：以为从偶，开平方，得积（S）．译成现代式子是这个式子称为秦九韶三斜求积公式；已知三角形的三边分别为5，6，7时，则面积为_________，最小角的余弦值为_________．‎ ‎12．复数（i为虚数单位），则_________，_________．‎ ‎13．二项式的展开式的所有项的系数和_________，展开式中有理项的项数为_________．‎ ‎14．在矩形ABCD中，，，P为矩形ABCD所在平面上一点，满足，则的最大值是_________，最大值是_________．‎ ‎15．将6个相同的球全部放入甲、乙、丙三个盒子里，每个盒子最多放入3个球，共有_________种不同的放法．‎ ‎16．已知点P为抛物线上的动点，过点P作圆的切线，切点为A，则PA的最小值为_________．‎ ‎17．已知函数，当时，的最大值为，则的最小值为_________．‎ 三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤．‎ ‎18．（本小题满分14分）‎ 已知函数．‎ ‎（1）求函数的最小正周期和对称轴；‎ ‎（2）若，求的取值范围．‎ ‎19．（本小题满分15分）‎ 四棱锥，底面ABCD为菱形，侧面PBC为正三角形，平面平面ABCD，，点M为AD中点．‎ ‎（1）求证：；‎ ‎ ‎ ‎（2）若点N是线段PA上的中点，求直线MN与平面PCM所成角的正弦值．‎ ‎20．（本小题满分15分）‎ 已知公差不为0的等差数列满足：，，，成等比数列，数列满足：，,‎ ‎（1）求数列的通项公式；‎ ‎（2）记数列，数列的前n项和为，证明：．‎ ‎21．（本小题满分15分）‎ 如图，已知椭圆经过和，过原点的一条直线l交椭圆于A，B两点（A在第一象限），椭圆C上点D满足，连直线BD与x轴、y轴分别交于M、N两点，的重心在直线的左侧．‎ ‎（1）求椭圆的标准方程；‎ ‎（2）记、面积分别为、，求的取值范围．‎ ‎22．（本小题满分15分）‎ ‎ ‎ 已知．‎ ‎（1）当时，求的单调区间；‎ ‎（2）当时，求证：；‎ ‎（3）满足（2）条件下的任意，，求证：．‎ ‎2019学年第二学期“山水联盟”高考模拟考试 数学学科参考答案 一、选择题：本题考查基本知识和基本运算．每小题4分，满分40分．‎ ‎1-5 DAADB 6-10 CCBDC 二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分．‎ ‎11．； 12．1； 13．243；3 14．5；‎ ‎15．10 16．1 17．5‎ 三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤．‎ ‎18．（本小题满分14分）‎ 解：（1）因为 所以的最小正周期．‎ 由得，‎ 故的对称轴为．‎ ‎（2）因为，所以，‎ 即，‎ ‎ ‎ 所以，‎ 即，‎ 即的取值范围．‎ ‎19．（本小题满分15分）‎ 解：（1）连AC，由题知为等边三角形，‎ 因为M为AD中点，所以，‎ 又，所以，‎ 而面面PBC，且面面，面ABCD，‎ 所以面PBC，故．‎ ‎（2）法一：设，取BC中点O，，，，，‎ 记MN与平面PCM所成角为，‎ 因为点N是线段PA上的中点，‎ 所以点N到平面PCM的高h是点A到平面PCM的高的一半，‎ ‎，，，‎ 由CM⊥面PBC，所以面面PBC，‎ 点O到时平面PCM的高为，‎ 所以点A到平面PCM的高与点O到时平面PCM的高相等且为，‎ ‎∴，‎ ‎ ‎ ‎．‎ 所以直线MN与平面PCM所成角的正弦值为．‎ 法二：取BC中点O，连AO，PO，以OC，OA，OP为x，y，z轴建立空间直角坐标系，‎ 设 所以，，，，，，‎ ‎．‎ 设面PCM的法向量为，‎ 由，得，取，‎ 设BN与面PCM所成角为，‎ 则，‎ 故MN与面PCM所成角的正弦值为．‎ ‎20．（本小题满分15分）‎ 解：（1）设等差数列的公差为．‎ ‎ ‎ ‎∵，，成等比数列，‎ ‎∴，即，‎ 整理得：．‎ 又，解得，．‎ ‎（2）∵，‎ ‎∴单调递增，，‎ ‎∴．‎ 又得：‎ 即，‎ 又，‎ ‎．‎ 故．‎ ‎∴．‎ ‎21．（本小题满分15分）‎ ‎ ‎ 解：（1）椭圆的标准方程．‎ ‎（2），，，，‎ ‎．‎ 记AD中点为E，，，，‎ ‎．‎ 又∵，∴，‎ ‎，∴，轴，N为BM中点，‎ ‎，．‎ ‎∵的重心在直线的左侧．‎ ‎∴，，‎ ‎，，‎ ‎∴，‎ ‎∴，‎ ‎ ‎ ‎∴．‎ ‎22．（本小题满分15分）‎ 解：（1）当时，，‎ ‎，‎ 令，，‎ ‎∴，，‎ ‎，，‎ ‎∴在单调递增，在单调递减．‎ ‎（2）当时，，‎ ‎，‎ 要证：‎ ‎．‎ 设，‎ 即证：．‎ 当时，时，，‎ 显然成立．‎ 当时，时，，‎ ‎ ‎ ‎．‎ 设，‎ ‎，‎ 先证：，‎ ‎．‎ ‎，在单调递减，，‎ ‎∴，‎ 在恒成立．‎ ‎∴，即证毕．‎ ‎（3）设，，‎ 在单调递增，‎ ‎∵，‎ ‎∴，‎ ‎，‎ 同理，‎ 相加得，‎ ‎ ‎ 即证毕．‎