2020届二轮复习立体几何中最值问题学案（全国通用） 5页

专题04 立体几何中最值问题 一．方法综述 高考试题将趋于关注那些考查生运用运动变化观点处理问题的题目，而几何问题中的最值与范围类问题，既可以考查生的空间想象能力，又考查运用运动变化观点处理问题的能力，因此，将是有中等难度的考题．此类问题，可以充分考查图形推理与代数推理，同时往往也需要将问题进行等价转化，比如求一些最值时，向平面几何问题转化，这些常规的降维操作需要备考时加强关注与训练．‎ 立体几何中的最值问题一般涉及到距离、面积、体积、角度等四个方面,此类问题多以规则几何体为载体,涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等,题目较为综合,解决此类问题一般可从三个方面思考：一是函数法,即利用传统方法或空间向量的坐标运算,建立所求的目标函数,转化为函数的最值问题求解；二是根据几何体的结构特征，变动态为静态，直观判断在什么情况下取得最值；三是将几何体平面化，如利用展开图，在平面几何图中直观求解。‎ 二．解题策略 类型一 距离最值问题 ‎【例1】如图，矩形，矩形，正方形两两垂直，且，若线段上存在点使得，则边长度的最小值为（ ）‎ A. 4 B. C. D. ‎ ‎【答案】D 又，所以 ‎.显然且.所以.‎ 因为，所以.所以当， 取得最小值12.所以的最小值为.‎ 故选D.‎ ‎【指点迷津】利用图形的特点，建立空间直角坐标系，设长度为及点P的坐标，求的坐标，根据两向量垂直，数量积为0，得到函数关系式，利用函数求其最值。&‎ 举一反三 ‎1、如图，在棱长为1的正方体ABCD-A1B1C1D1中，点E、F分别是棱BC，CC1的中点，P是侧面BCC1B1内一点，若A1P∥平面AEF，则线段A1P长度的取值范围是_____。‎ ‎【答案】 ‎ ‎∵P是侧面BCC1B1内一点，且A1P∥平面AEF，∴点P必在线段MN上。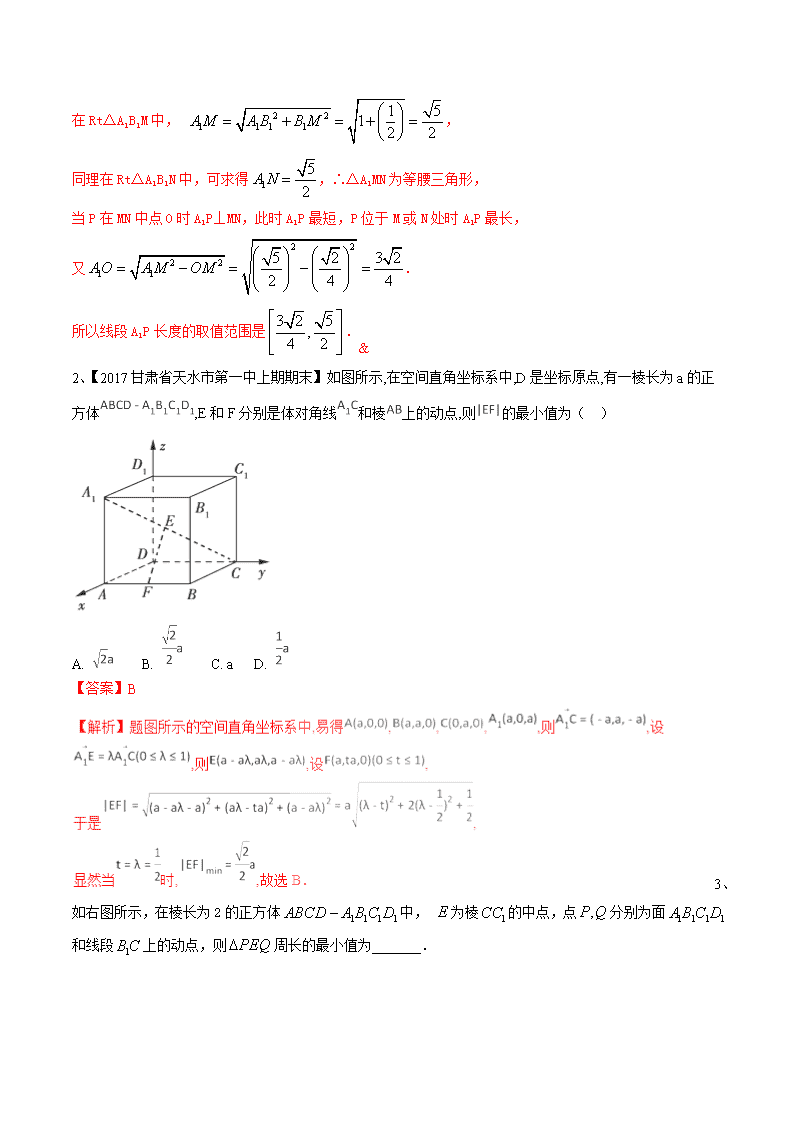‎ 在Rt△A1B1M中， ，‎ 同理在Rt△A1B1N中，可求得，∴△A1MN为等腰三角形，‎ 当P在MN中点O时A1P⊥MN，此时A1P最短，P位于M或N处时A1P最长，‎ 又.‎ 所以线段A1P长度的取值范围是．&‎ ‎2、【2017甘肃省天水市第一中上期期末】如图所示,在空间直角坐标系中,D是坐标原点,有一棱长为a的正方体,E和F分别是体对角线和棱上的动点,则的最小值为（ ）‎ A. B. C. a D. ‎ ‎【答案】B ‎ 3、如右图所示，在棱长为2的正方体中， 为棱的中点，点分别为面和线段上的动点，则周长的最小值为_______． ‎ ‎【答案】‎ ‎【解析】将面与面折成一个平面，设E关于的对称点为M，E关于 对称点为N,则周长的最小值为.&‎ 类型二 面积的最值问题 ‎【例2】已知球是正三棱锥（底面为正三角形，顶点在底面的射影为底面中心）的外接球， ， ，点在线段上，且，过点作圆的截面，则所得截面圆面积的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】B 关注.‎