衡水独家秘籍之2019高中期末复习 专题二 常见分段函数问题求解策略 7页

衡水独家秘籍之2019高中期末复习 专题二常见分段函数问题求解策略 ‎【方法综述】‎ 分段函数：(1)若函数在其定义域的不同子集上，因对应关系不同而分别用几个不同的式子来表示，这种函数称为分段函数.‎ ‎(2)分段函数的定义域等于各段函数的定义域的并集，其值域等于各段函数的值域的并集，分段函数虽由几个部分组成，但它表示的是一个函数.‎ 分段函数是一类特殊的函数，有着广泛的应用，课本中并没有进行大篇幅的介绍，但是它是高考的必考内容，下面就常见分段函数问题解决方法举例说明．‎ ‎1．求分段函数的函数值 例1.已知函数，则=‎ 解：因为,所以.‎ 解题策略　求分段函数的函数值时，关键是判断所给出的自变量所处的区间，再代入相应的解析式；另一方面，如果题目中含有多个分层的形式，则需要由里到外层层处理．‎ ‎2．求解分段函数的解析式 例2.某移动公司采用分段计费的方法来计算话费，月通话时间x(分钟)与相应话费y(元)之间的函数图象如图所示．则：(1)月通话为50分钟时，应交话费多少元；(2)求y与x之间的函数关系式．‎ 解：　(1)由题意可知当0＜x≤100时，设函数的解：析式y＝kx，又因过点(100,40)，得解析式为y＝x，当月通话为50分钟时，0＜50＜100，‎ 所以应交话费y＝×50＝20(元)．‎ ‎(2)当x＞100时，设y与x之间的函数关系式为y＝kx＋b，由图知x＝100时，y＝40；x＝200时，y＝60.‎ 则有解：得 所以解：析式为y＝x＋20，‎ 故所求函数关系式为y＝ 解题策略　以收费为题材的数学问题多以分段函数的形式出现在试题中，解决此类问题的关键是正确地理解：题目(或图象)给出的信息，确定合适的数学模型及准确的自变量的分界点．‎ ‎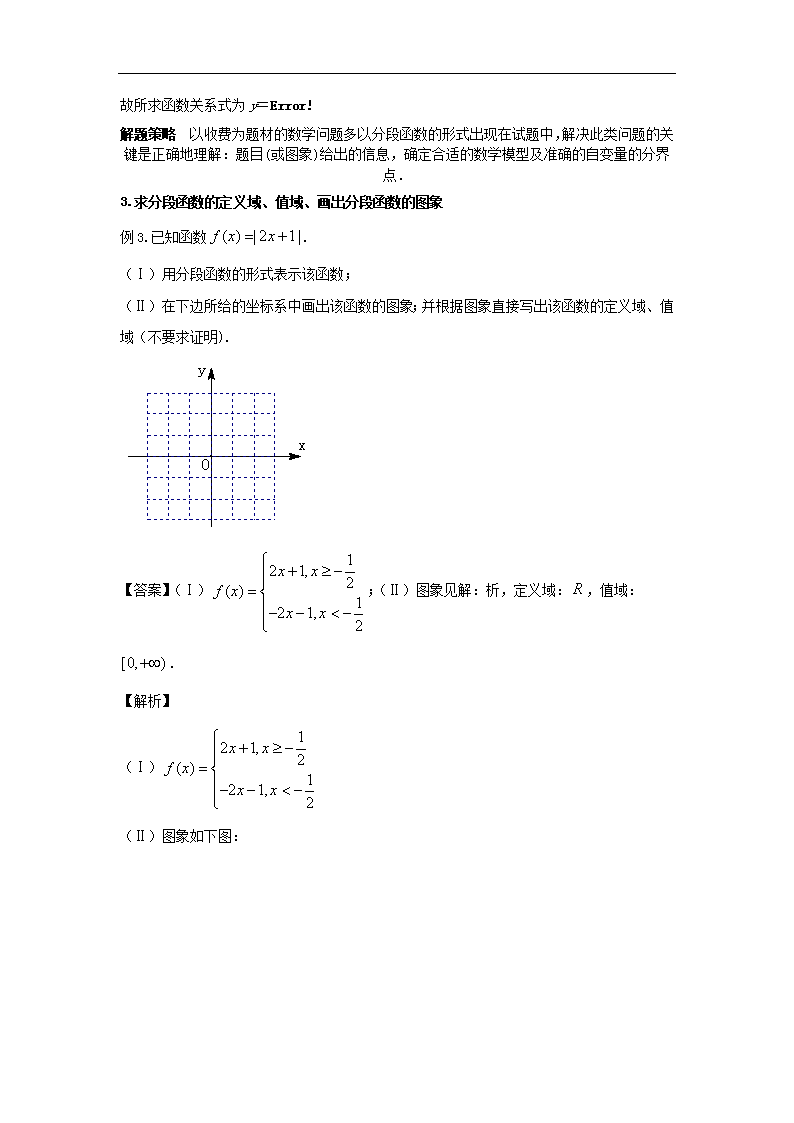3.求分段函数的定义域、值域、画出分段函数的图象 例3.已知函数.‎ ‎（Ⅰ）用分段函数的形式表示该函数；‎ ‎（Ⅱ）在下边所给的坐标系中画出该函数的图象；并根据图象直接写出该函数的定义域、值域（不要求证明).‎ ‎【答案】（Ⅰ）；（Ⅱ）图象见解：析，定义域：，值域：.‎ ‎【解析】‎ ‎（Ⅰ）‎ ‎（Ⅱ）图象如下图：‎ 观察得到定义域为，值域为.‎ 解题策略 ‎（1）分段函数有几段，其图象就由几条曲线组成，作图的关键是根据定义域的不同分别由表达式作出其图象，作图时一要注意每段自变量的取值范围，二要注意判断函数图象每段端点的虚实．‎ ‎（2）分段函数的定义域是各段函数解：析式中自变量取值集合的并集；分段函数的值域是各段函数值集合的并集．‎ ‎【针对训练】‎ ‎1．已知函数fx=‎x‎2‎‎-x,x≤1,‎‎1‎‎1-x‎,x>1,‎则ff‎-1‎的值为（ ）‎ A． ‎-1‎ B． ‎1‎‎5‎ C． ‎-‎‎1‎‎5‎ D． 1‎ ‎【答案】A ‎【解析】‎ 由题得f(-1)=‎(-1)‎‎2‎‎-(-1)=1+1=2,∴f(f(-1))=f(2)=‎1‎‎1-2‎=-1‎.‎ 故答案为：A ‎2. 已知符号函数sgnx=‎1,‎‎0,‎‎-1,‎x>0‎x=0‎x<0‎ ,fx是R上的增函数，gx=fx-fax，a>1‎则（ ）‎ A． sgngx‎=‎sgnx B． sgngx‎=‎- sgnx C． sgngx‎=‎sgn fx D． sgngx‎=‎- sgn ‎fx ‎【答案】B ‎【解析】‎ 当x>0‎时，xax，由单调性：g(x)>0‎，此时sgn[g(x)]=1=-sgnx，‎ 所以sgn[g(x)]=-sgnx.‎ 故选B.‎ ‎3.已知函数满足，则（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】‎ ‎∵‎ 依此类推，得，∴选B.‎ ‎4．已知函数，若，且，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ 作出函数f(x)的图象如图，‎ 若m0得1