2013-2017高考数学分类汇编-文科 第二章 函数 第3节 二次函数与幂函数 3页

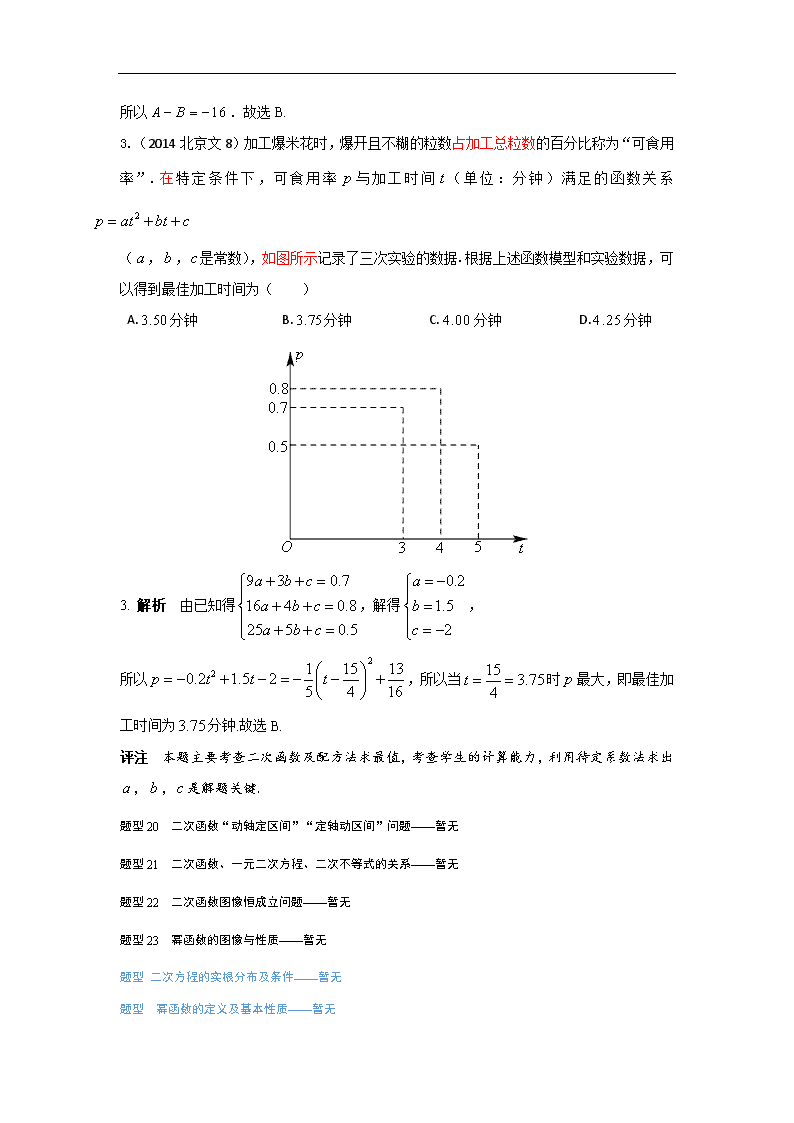
第二章 函数 第3节 二次函数与幂函数 题型19 二次函数图像及应用 ‎1. (2013浙江文7）已知，函数.若，则（ ）.‎ A. ， B. ， ‎ C. ， D. ，‎ ‎1.分析 根据条件可确定函数图象的开口方向和对称轴，化简即得.‎ 解析 因为，所以函数图象应开口向上，即，且其对称轴为，即，所以，故选A.‎ ‎2. (2013辽宁文12）已知函数，.设，，表示中的较大值，表示中的较小值，记得最大值为，得最小值为，则（ ）.‎ A. B. ‎ C. D. ‎ ‎2.分析：根据二次函数图象的特征解决．‎ 解析 由，得，所以当和时，两函数值相等．图象为开口向上的抛物线，图象为开口向下的抛物线，两图象在和处相交，则 所以，,‎ 所以．故选B.‎ 3. ‎（2014北京文8）加工爆米花时，爆开且不糊的粒数占加工总粒数的百分比称为“可食用 率”.在特定条件下，可食用率与加工时间（单位：分钟）满足的函数关系 ‎ ‎（，，是常数），如图所示记录了三次实验的数据.根据上述函数模型和实验数据，可 以得到最佳加工时间为（ ）‎ ‎ A.分钟 B.分钟 C.分钟 D.分钟 ‎3. 解析 由已知得，解得，‎ 所以，所以当时最大，即最佳加工时间为分钟.故选B.‎ 评注 本题主要考查二次函数及配方法求最值，考查学生的计算能力，利用待定系数法求出，，是解题关键.‎ 题型20 二次函数“动轴定区间”“定轴动区间”问题——暂无 题型21 二次函数、一元二次方程、二次不等式的关系——暂无 题型22 二次函数图像恒成立问题——暂无 题型23 幂函数的图像与性质——暂无 题型 二次方程的实根分布及条件——暂无 题型 幂函数的定义及基本性质——暂无 题型 幂函数性质的综合应用——暂无 题型 二次方程的实根分布及条件——暂无