- 200.00 KB
- 2021-06-30 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
不等式
1.如果af(1)的解集是( )
A.(-3,1)∪(3,+∞) B.(-3,1)∪(2,+∞)
C.(-1,1)∪(3,+∞) D.(-∞,-3)∪(1,3)
【解析】由题意得,f(1)=3,所以f(x)>f(1)=3,即f(x)>3,
如果x<0,则x+6>3,可得-33,可得x>3或0≤x<1.
综上,不等式的解集为(-3,1)∪(3,+∞).
故选A.
【答案】A
4.若关于x的不等式ax-b>0的解集是(-∞,-2),则关于x的不等式>0的解集为( )
A.(-2,0)∪(1,+∞) B.(-∞,0)∪(1,2)
C.(-∞,-2)∪(0,1) D.(-∞,1)∪(2,+∞)
【解析】关于x的不等式ax-b>0的解集是(-∞,-2),∴a<0,=-2,∴b=-2a,∴=.∵a<0,∴<0,解得x<0或10,≤a恒成立,则a的取值范围是( )
A.a≥ B.a>
C.a< D.a≤
【解析】因为对任意x>0,≤a恒成立,
所以对x∈(0,+∞),a≥max,
而对x∈(0,+∞),=≤=,
当且仅当x=时等号成立,∴a≥.
【答案】A
6.若关于x,y的不等式组表示的平面区域是等腰直角三角形区域,则其表示的区域面积为( )
A.或 B.或
C.1或 D.1或
【解析】由不等式组表示的平面区域是等腰直角三角形区域,得k=0或1,当k=0时,表示区域的面积为;当k=1时,表示区域的面积为,故选A.
【答案】A
7.设变量x,y满足约束条件则目标函数z=2x+5y的最小值为( )
A.-4 B.6
C.10 D.17
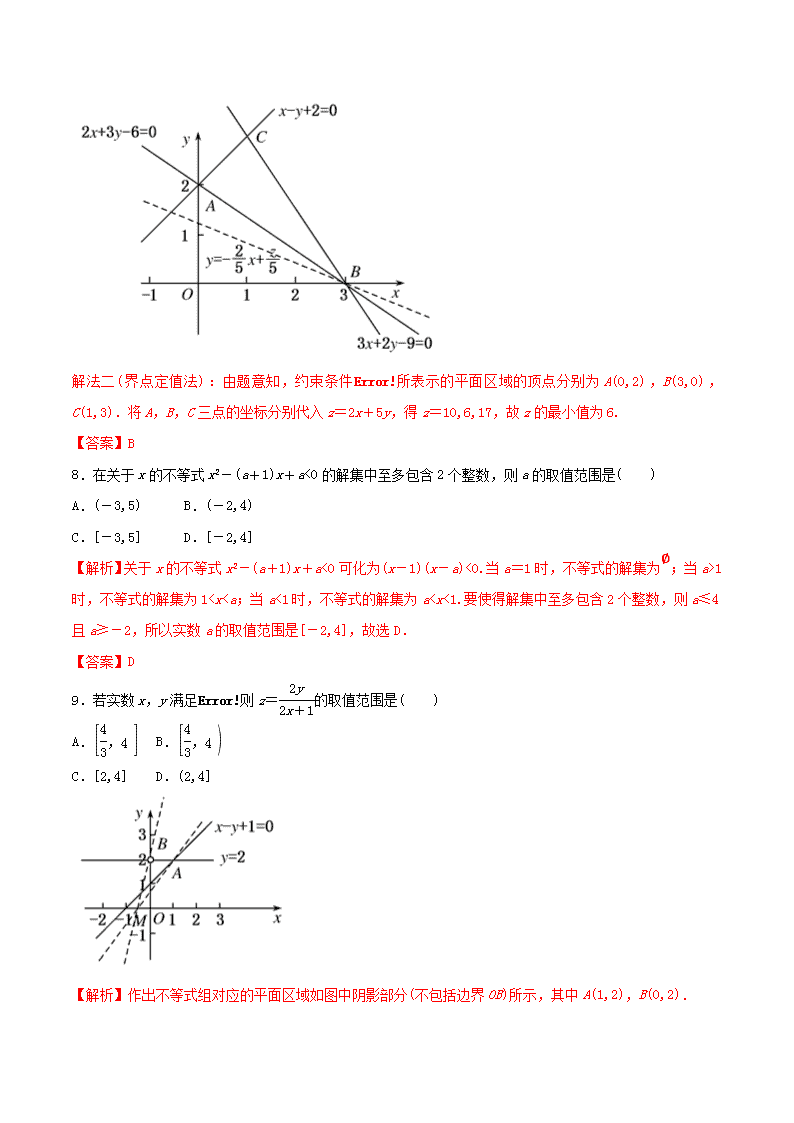
【解析】解法一(图解法):已知约束条件所表示的平面区域为下图中的阴影部分(包含边界),其中A(0,2),B(3,0),C(1,3).根据目标函数的几何意义,可知当直线y=-x+过点B(3,0)时,z取得最小值2×3+5×0=6.
解法二(界点定值法):由题意知,约束条件所表示的平面区域的顶点分别为A(0,2),B(3,0),C(1,3).将A,B,C三点的坐标分别代入z=2x+5y,得z=10,6,17,故z的最小值为6.
【答案】B
8.在关于x的不等式x2-(a+1)x+a<0的解集中至多包含2个整数,则a的取值范围是( )
A.(-3,5) B.(-2,4)
C.[-3,5] D.[-2,4]
【解析】关于x的不等式x2-(a+1)x+a<0可化为(x-1)(x-a)<0.当a=1时,不等式的解集为∅;当a>1时,不等式的解集为10,b>0,且2a+b=ab,则a+2b的最小值为( )
A.5+2 B.8
C.5 D.9
【答案】D
11.已知实数x,y满足且z=x+y的最大值为6,则(x+5)2+y2的最小值为( )
A.5 B.3
C. D.
【解析】如图,作出不等式组对应的平面区域,
由z=x+y,得y=-x+z,平移直线y=-x,由图可知当直线y=-x+z经过点A时,直线y=-x+z在y轴上的截距最大,此时z最大,为6,即x+y=6.由得A(3,3),
∵直线y=k过点A,∴k=3.
(x+5)2+y2的几何意义是可行域内的点(x,y)与D(-5,0)的距离的平方,由可行域可知,[(x+5)2+y2]min等于D(-5,0)到直线x+2y=0的距离的平方.
则(x+5)2+y2的最小值为2=5.故选A.
【答案】A
12.若正数a,b满足:+=1,则+的最小值为( )
A.16 B.9
C.6 D.1
【解析】∵正数a,b满足+=1,∴a+b=ab,=1->0,=1->0,∴b>1,a>1,则+≥2=2=6,∴+的最小值为6,故选C.
【答案】C
13.若x>0,y>0,则“x+2y=2”的一个充分不必要条件是( )
A.x=y B.x=2y
C.x=2且y=1 D.x=y或y=1
【解析】∵x>0,y>0,∴x+2y≥2,当且仅当x=2y时取等号.故“x=2,且y=1”是“x+2y=2”的充分不必要条件.故选C.
【答案】C
14.已知实数x,y满足约束条件则z=x-2y的最大值是( )
A. B.
C.32 D.64
【解析】解法一 作出不等式组表示的平面区域,如图中阴影部分所示,设u=x-2y,由图知,当u=x-2y经过点A(1,3)时取得最小值,即umin=1-2×3=-5,此时z=x-2y取得最大值,即zmax=-5=32,故选C.
解法二 作出不等式组表示的平面区域,如图中阴影部分所示,易知z=x-2y的最大值在区域的顶点处取得,只需求出顶点A,B,C的坐标分别代入z=x-2y,即可求得最大值.联立得解得A(1,3),代入可得z=32;联立得解得B,代入可得z=;联立得解得C(-2,0),代入可得z=4.通过比较可知,在点A(1,3)处,z=x-2y取得最大值32,故选C.
【答案】C
15.某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得的最大利润为( )
甲
乙
原料限额
A/吨
3
2
12
B/吨
1
2
8
A.15万元 B.16万元
C.17万元 D.18万元
【解析】设生产甲产品x吨,乙产品y吨,获利润z万元,由题意可知,z=3x+4y,画出可行域如图中阴影部分所示,直线z=3x+4y过点M时,z=3x+4y取得最大值,
由得
∴M(2,3),故z=3x+4y的最大值为18,故选D.
【答案】D
16.已知函数f(x)=x++2的值域为(-∞,0]∪[4,+∞),则a的值是( )
A. B.
C.1 D.2
【解析】由题意可得a>0,①当x>0时,f(x)=x++2≥2+2,当且仅当x=时取等号;②当x<0时,f(x)=x++2≤-2+2,当且仅当x=-时取等号.所以解得a=1,故选C.
【答案】C
17.不等式组的解集记为D.有下面四个命题:
p1:∀(x,y)∈D,x-2y≥2;
p2:∃ (x,y)∈D,x-2y≥3;
p3:∀(x,y)∈D,x-2y≥;
p4:∃(x,y)∈D,x-2y≤-2.
其中的真命题是( )
A.p2,p3 B.p1,p4
C.p1,p2 D.p1,p3
【解析】不等式组表示的可行域为如图所示的阴影部分,
由解得所以M.由图可知,当直线z=x-2y过点M处时,z取得最小值,且zmin=-2×=
,所以真命题是p2,p3,故选A.
【答案】A
18.已知实数x,y满足且z=x+y的最大值为6,则(x+5)2+y2的最小值为( )
A.5 B.3
C. D.
【解析】作出不等式组表示的平面区域如图中阴影部分所示,由z=x+y,得y=-x+z,平移直线y=-x,由图形可知当直线y=-x+z经过点A时,直线y=-x+z的纵截距最大,此时z最大,最大值为6,即x+y=6.由得A(3,3),∵直线y=k过点A,∴k=3.(x+5)2+y2的几何意义是可行域内的点与D(-5,0)的距离的平方,数形结合可知,(-5,0)到直线x+2y=0的距离最小,可得(x+5)2+y2的最小值为2=5.故选A.
【答案】A
19.对于任意实数x,不等式(a-2)x2-2(a-2)x-4<0恒成立,则实数a的取值范围是( )
A.(-∞,2) B.(-∞,2]
C.(-2,2) D.(-2,2]
【解析】当a=2时,原不等式为-4<0,恒成立;当a≠2时,函数y=(a-2)x2-2(a-2)x-4是二次函数,若不等式恒成立,则a-2<0且Δ=4(a-2)2+16(a-2)<0,解得-29
【答案】C
22.设0b3 B.<
C.ab>1 D.lg(b-a)0的解集是________________.
【解析】原不等式可转化为|x|2-3|x|+2>0,解得|x|<1或|x|>2,所以x∈(-∞,-2)∪(-1,1)∪(2,+∞).
【答案】(-∞,-2)∪(-1,1)∪(2,+∞)
24.已知函数f(x)=sinπx(0