高中数学必修3教案：1_1_2（2）程序框图与算法的基本逻辑结构 5页

1. 1.2 程序框图与算法的基本逻辑结构（二） ———条件结构和循环结构 学习目标 1、更进一步理解算法， 2、掌握算法的条件结构和循环结构， 3、掌握画程序框图的基本规则，能正确画出程序框图.学会灵活、正确地画程序 框图。 重点难点 重点：条件结构和循环结构的应用。 难点：综合运用这些知识正确地画出程序框图。 学法指导 顺序结构是任何一个算法都离不开的基本逻辑结构，在一些算法中，有些步 骤只有在一定条件下才会被执行，有些步骤在一定条件下会被重复执行，这需要 我们对算法的逻辑结构作进一步探究. 条件结构和循环结构的基本特征： （1）程序框图中必须有两个起止框，穿插输入、输出框和处理框，一定有判断 框. （2）循环结构中包含条件结构，条件结构中不含循环结构. （3）条件结构和循环结构的程序框图各有两种形式，相互对立统一. 知识链接 基本程序框图的画法与含义。 问题探究 知识探究（一）：算法的条件结构 思考 1:在某些问题的算法中，有 些步骤只有在一定条件下才会被执 行，算法的流程因条件是否成立而变 化.在算法的程序框图中，由若干个在 一定条件下才会被执行的步骤组成的 逻辑结构，称为 ，用程 序框图可以表示为下面两种形式： 你如何理解这两种程序框图的共性和 个性？ 思考 2:判断“以任意给定的 3 个 正实数为三条边边长的三角形是否存 在”的算法步骤如何设计？ 第一步， 第二步， 思考 3:你能画出这个算法的程序 框图吗？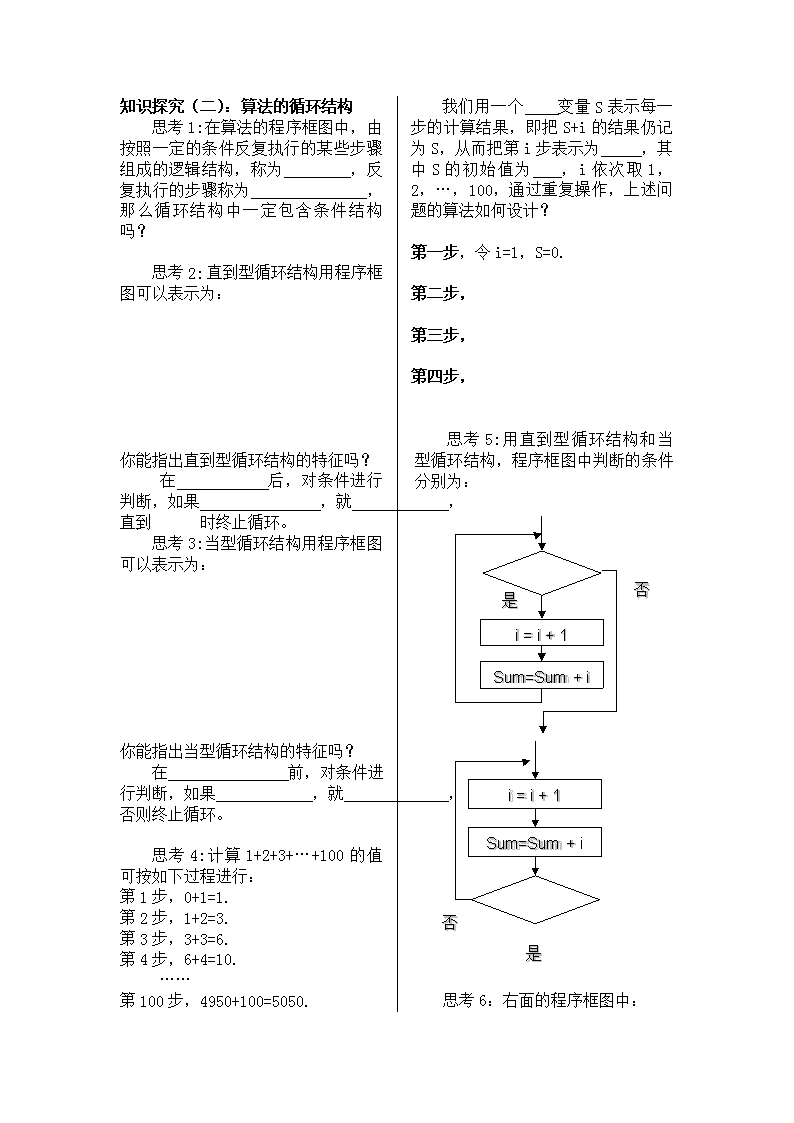 知识探究（二）：算法的循环结构 思考 1:在算法的程序框图中，由 按照一定的条件反复执行的某些步骤 组成的逻辑结构，称为 ，反 复执行的步骤称为 ， 那么循环结构中一定包含条件结构 吗？ 思考 2: 直到型循环结构用程序 框图可以表示为： 你能指出直到型循环结构的特征吗？ 在 后，对条件进行 判断， 如果 ， 就 ，直到 时终止 循环。 思考 3:当型循环结构用程序框图 可以表示为： 你能指出当型循环结构的特征吗？ 在 前，对条件进 行 判 断 ， 如 果 ， 就 ，否则终止循环。 思考4:计算1+2+3+…+100的值可 按如下过程进行： 第 1 步，0+1=1. 第 2 步，1+2=3. 第 3 步，3+3=6. 第 4 步，6+4=10. …… 第 100 步，4950+100=5050. 我们用一个 变量 S 表示每一 步的计算结果，即把 S+i 的结果仍记 为 S，从而把第 i 步表示为 ，其 中 S 的初始值为 ，i 依次取 1，2，…， 100，通过重复操作，上述问题的算法 如何设计？ 第一步，令 i=1，S=0. 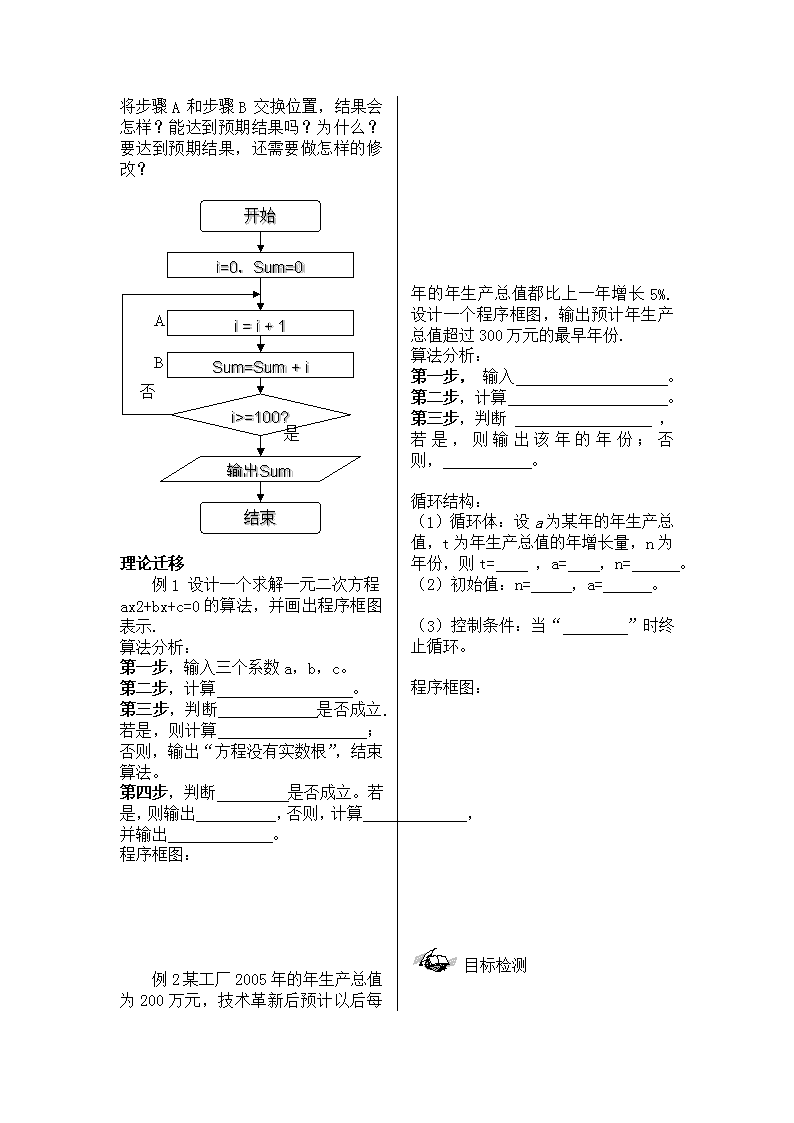第二步， 第三步， 第四步， 思考 5:用直到型循环结构和当型 循环结构，程序框图中判断的条件分 别为： ii == ii ++ 11 Sum=SumSum=Sum ++ ii 否否是是 ii == ii ++ 11 Sum=SumSum=Sum ++ i 是是 否否 思考 6：右面的程序框图中： 将步骤 A 和步骤 B 交换位置，结果会 怎样？能达到预期结果吗？为什么？ 要达到预期结果，还需要做怎样的修 改？ 理论迁移 例 1 设计一个求解一元二次方程 ax2+bx+c=0 的算法，并画出程序框图 表示. 算法分析： 第一步，输入三个系数 a，b，c。 第二步，计算 。 第三步，判断 是否成立. 若是，则计算 ； 否则，输出“方程没有实数根”，结束 算法。 第四步，判断 是否成立。若 是，则输出 ，否则，计 算 ， 并 输 出 。 程序框图： 例2 某工厂 2005年的年生产总值 为 200 万元，技术革新后预计以后每 年的年生产总值都比上一年增长 5%. 设计一个程序框图，输出预计年生产 总值超过 300 万元的最早年份. 算法分析： 第一步， 输入 。 第二步，计算 。 第三步，判断 ， 若 是 ， 则 输 出 该 年 的 年 份 ； 否 则， 。 循环结构： （1）循环体：设 a 为某年的年生产总 值，t 为年生产总值的年增长量，n 为 年份，则 t= ，a= ，n= 。 （2）初始值：n= ，a= 。 （3）控制条件：当“ ”时终 止循环。 程序框图： B A 结束结束 输出输出SumSum i=0i=0，，Sum=0Sum=0 开始开始 ii == ii ++ 11 Sum=SumSum=Sum ++ ii i>=100?i>=100? 否 是 目标检测 1、如图（1）所示程序的输出结果为 s=132, 则判断中应填 . A、i≥10？ B、i≥11？ C、i≤11？ D、i≥12？ 2、如图(2)程序框图箭头 b 指向①处 时，输出 s=__________. 箭 头 b 指 向 ② 处 时 ， 输 出 s=__________ 3、如图(3)是为求 1~1000 的所有偶数 的和而设计的一个程序空白框图，将 空白处补上。 ①__________。②__________。 4 ． 如 图 （ 4 ） 程 序 框 图 表 达 式 中 N=__________。 5、已知函数   2 1 2 1 xf x x     ( 0) ( 0) x x   , 设计一个求函数值的算法,并画出其 程序框图 N （1） 开始 i=1 s=0 s=s+i i=i+1 i≤5? Y ① ② b N 结束（2） 输出 s s=s×i 输出 s 结束 开始 Y i=12,s=11 i=i-1 6、假设超市购物标价不超过 100 时按 九折付款，如标价超过 100 元，则超 过部分按七折收费，写出超市收费的 算法，并画出流程图。 总结反思 1、条件结构：是根据指定打件选择执 行不同指令的控制结构。根据给定的 条件 P 是否成立而选择执行 A 框或 B 框。无论 P 条件是否成立，只能执行 A 框或 B 框之一，不可能同时执行 A 框 和 B 框，也不可能 A 框、B 框都不执 行。 2．循环结构要在某个条件下终止循 环，这就需要条件结构来判断。因此， 循环结构中一定包含条件结构。 3．在循环结构中都有一个计数变量 和累加变量。计数变量用于记录循环 次数，累加变量用于输出结果。计数 变量和累加变量一般是同步执行的， 累加一次，计数一次。 4．画循环结构流程图前： ①确定循环变量和初始条件； ②确定算法中反复执行的部分，即循 环体； ③确定循环的转向位置； ④确定循环的终止条件. 结束 开始 i=2 s=0 i≤1000? 是 （1） （2） 否 输出 s （3） 开始 N=1 I=2 N=N×I I=I+1 N I≤5? 输 入 结束 Y （4）