山西省太原市第二十一中学2019-2020学年高一上学期期中考试数学试题 含答案 8页

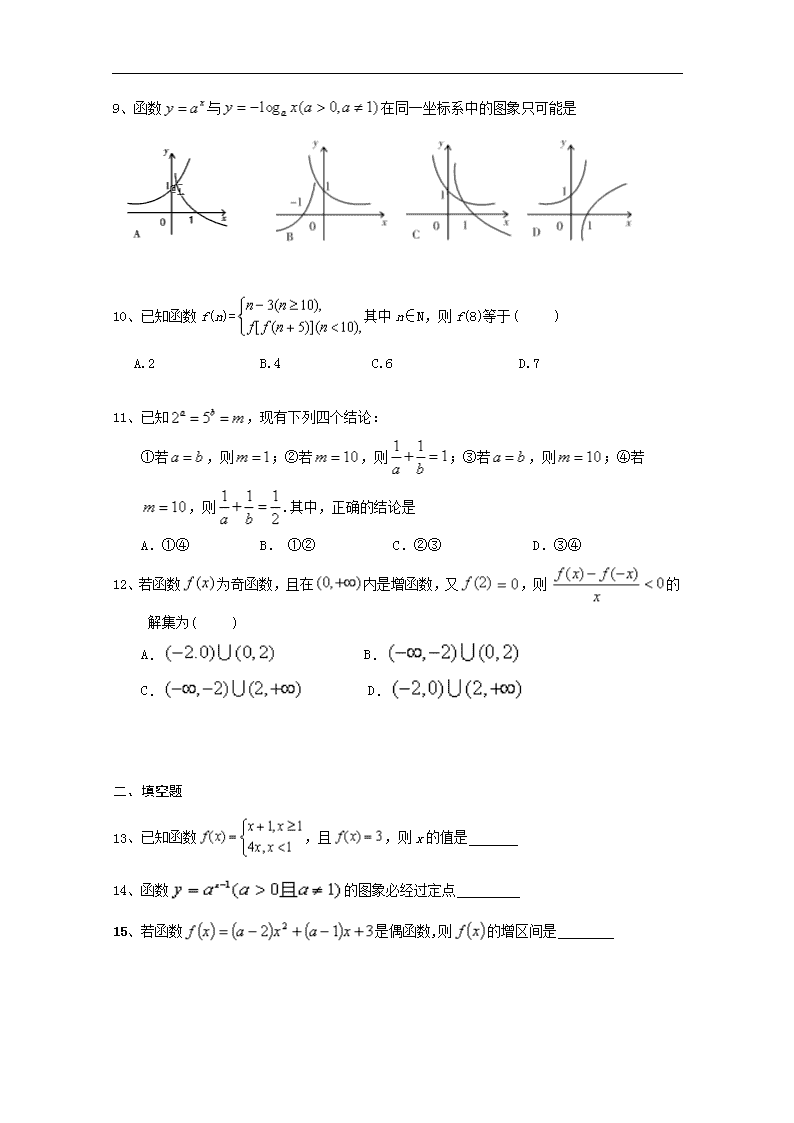
数学试题 ‎ ‎ 一、选择题 ‎ ‎1、设集合，， ，则(A∩C)∪B＝(　　) A.  {2}  B.   {2,3} C.  {－1,2,3} D.  {1,2,3,4} ‎ ‎2、函数 的定义域是(　　) A. B. C. D.‎ ‎3、已知幂函数的图象经过点,则的值为(   )‎ A. B. C. D. 2‎ ‎4、下列函数中，既是奇函数又在区间上是增函数的是（ ）‎ A． B． C． D. ‎ ‎5、下列四组函数中，表示同一函数的是 ‎ A．与 B．与 C．与 D．与 ‎6、已知f（x）=3X+3－X，若f（a）=4，则f（2a）=（　　）‎ A．4 B．14 C．16 D．18 ‎ ‎7、已知,则之间的大小关系是（ ）‎ A. B. C. D. ‎ ‎8、下列函数中，值域是的是 A． B． C． D．‎ ‎9、函数与在同一坐标系中的图象只可能是 ‎ ‎ ‎10、已知函数f(n)=其中n∈N，则f(8)等于( )‎ A.2　　　　　　 B.4　　　　　　 C.6　　　　　　 D.7‎ ‎11、已知，现有下列四个结论：‎ ‎ ①若，则；②若，则；③若，则；④若 ，则.其中，正确的结论是 A．①④ B． ①② C．②③ D．③④‎ ‎12、若函数为奇函数，且在内是增函数，又，则的解集为( )‎ ‎ A． B．‎ C． D．‎ 二、填空题 ‎13、已知函数，且，则x的值是 ‎ ‎14、函数的图象必经过定点 ‎ ‎15、若函数是偶函数,则的增区间是 ‎ ‎16、已知函数是定义在R上的奇函数，若对任意给定的实数，不等式恒成立，则不等式的解集是_________.‎ 三、解答题 ‎17、已知全集，集合，．‎ ‎（1）当时，求集合和；‎ ‎（）若，求实数的取值范围．‎ ‎18、计算：（1）；‎ ‎（2）.‎ ‎19、函数f(x)是R上的奇函数，且当x>0时，函数的解析式为f(x)＝＋1.‎ ‎(1)用定义证明f(x)在(0，＋∞)上是减函数；‎ ‎(2)当x<0时，求函数f(x)的解析式．‎ ‎20、已知函数f（x）=x2+（2a﹣1）x﹣3．‎ ‎（1）当a=2，x∈[﹣2，3]时，求函数f（x）的值域；‎ ‎（2）若函数f（x）在[﹣1，3]上的最大值为1，求实数a的值 ‎21、已知函数是定义在上的奇函数，且． （1）求函数的解析式； （2）解关于t的不等式．‎ ‎22、已知函数.‎ ‎（1）设，当时，求函数的定义域，判断并证明函数的奇偶性；‎ ‎（2）是否存在实数，使函数在上单调递减，且最小值为1？若存在，求出的值；若不存在，请说明理由.‎ 数学试题答案 一、 选择题 ‎1、D 2、D 3、A 4、B 5、C 6、B 7、D 8、B 9、A 10、D 11、B 12、A 二、填空题 ‎13、2或 14、 15、 16、‎ 三、解答题 ‎17、解：，‎ ‎ （1）当时，，则 ‎ ，‎ 或；................................................. 5分 ‎ （）由有，‎ ‎ 当时，， ，‎ ‎ 当时，即时，且，‎ ‎ 则，有．‎ ‎ 综上所述，，即m的取值范围是............................................10分 ‎18、解：（1）原式=；..................................6分 ‎（2）‎ ‎ ‎ ‎ . ................................................................12分 ‎19、(1)设00时，f(x)＝＋1‎ 得：f(x1)－f(x2)＝(＋1)－(＋1)＝，‎ ‎∵00，x2－x1>0，‎ ‎∴f(x1)－f(x2)>0，即f(x1)>f(x2)，‎ ‎∴f(x)在(0，＋∞)上是减函数．‎ ‎(2)当x<0时，－x>0，‎ ‎∵x>0时， f(x)＝＋1，‎ ‎∴f(－x)＝＋1＝－＋1，‎ 又f(x)为奇函数， f(－x)＝－f(x)，‎ ‎∴－f(x)＝－＋1, f(x)＝－1，‎ ‎∴x>0时， f(x)＝－1.‎ ‎20、解：（1）当a=2时，f（x）=x2+3x﹣3=（x+）2﹣，‎ 又x∈[﹣2，3]，所以f（x）min=f（﹣）=﹣，‎ f（x）max=f（3）=15，所以值域为[﹣，15]．‎ ‎（2）对称轴为x=﹣．‎ ‎①当﹣≤1，即a≥﹣时，‎ f（x）max=f（3）=6a+3，‎ 所以6a+3=1，即a=﹣满足题意；‎ ‎②当﹣＞1，即a＜﹣时，‎ f（x）max=f（﹣1）=﹣2a﹣1，‎ 所以﹣2a﹣1=1，即a=﹣1满足题意．‎ 综上可知a=﹣或﹣1．‎ ‎21、（1）由奇函数的性质可知, ，∴,, ‎ ‎∵, ∴,‎ ‎ （2）由，且为增函数 ‎∴． 故不等式的解集为．‎ ‎22、解：（1）的定义域为，.............................3分 ‎ 为奇函数，证明略..............................................6分 ‎（2）不存在。‎ ‎ 假设存在实数满足条件，记，因，‎ ‎ 则在上单调递增，‎ ‎ 使函数在上单调递减，则，....................................8分 ‎ 由函数在上最小值为1，则有 ‎ ，不等式组无解，‎ ‎ 故不存在实数满足题意.............................................12分