湖北省2020届高三数学理一轮复习典型题专项训练：立体几何 25页

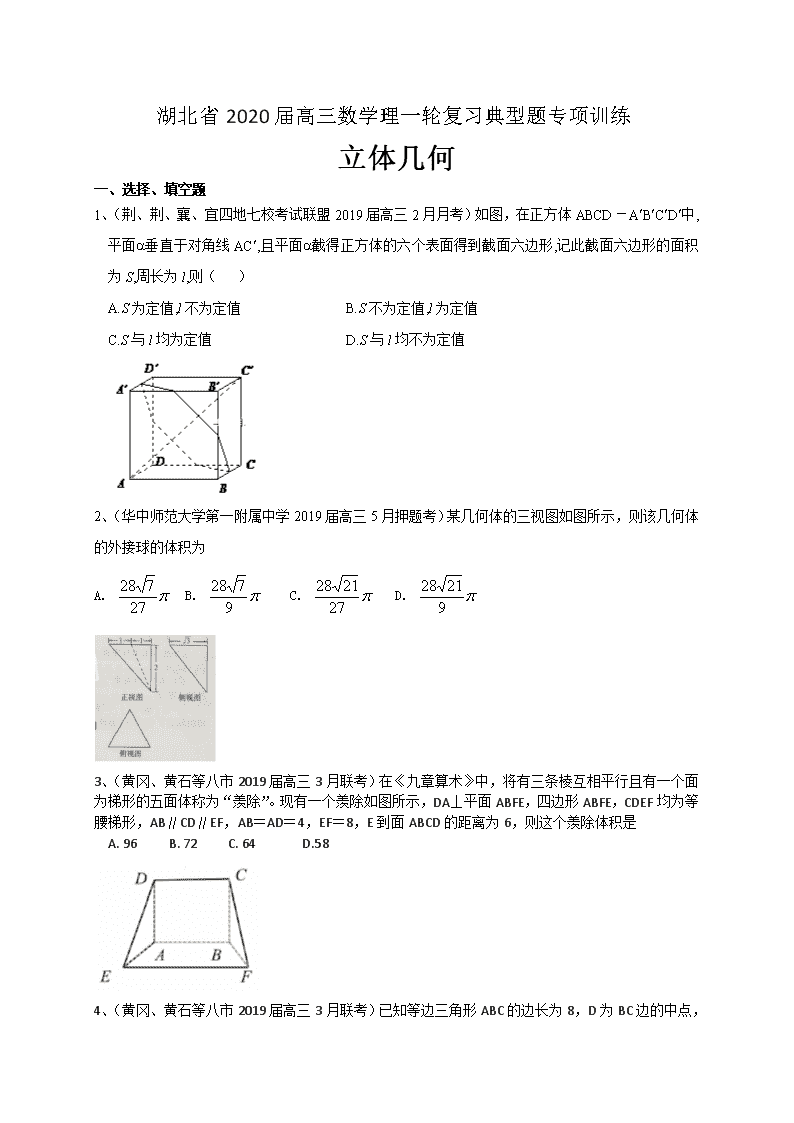
湖北省2020届高三数学理一轮复习典型题专项训练 立体几何 一、选择、填空题 ‎1、（荆、荆、襄、宜四地七校考试联盟2019届高三2月月考）如图，在正方体ABCD－A¢B¢C¢D¢中,平面a垂直于对角线AC¢,且平面a截得正方体的六个表面得到截面六边形,记此截面六边形的面积为S,周长为l,则（ ）‎ A.S为定值,l不为定值 B.S不为定值,l为定值 C.S与l均为定值 D.S与l均不为定值 ‎2、（华中师范大学第一附属中学2019届高三5月押题考）某几何体的三视图如图所示，则该几何体的外接球的体积为 A. B. 　　C. 　D. ‎ ‎3、（黄冈、黄石等八市2019届高三3月联考）在《九章算术》中，将有三条棱互相平行且有一个面为梯形的五面体称为“羡除”。现有一个羡除如图所示，DA⊥平面ABFE，四边形ABFE，CDEF均为等腰梯形，AB∥CD∥EF，AB＝AD＝4，EF＝8，E到面ABCD的距离为6，则这个羡除体积是 ‎ A. 96 　　B. ‎72 ‎　　C. 64　　　 D.58‎ ‎4、（黄冈、黄石等八市2019届高三3月联考）‎ 已知等边三角形ABC的边长为8，D为BC边的中点，沿AD将△ABC折成直二面角B－AD－C， 则三棱锥A－DCB的外接球的表面积为　　　　‎ ‎5、（黄冈中学、华师一附中等八校2019届高三第二次（3月）联考）如图,某多面体的三视图中正视图、侧视图和俯视图的外轮廓分别为直角三角形、直角梯形和直角三角形，则该多面体的各条棱中，最长的棱的长度为 ‎ A. B. C. 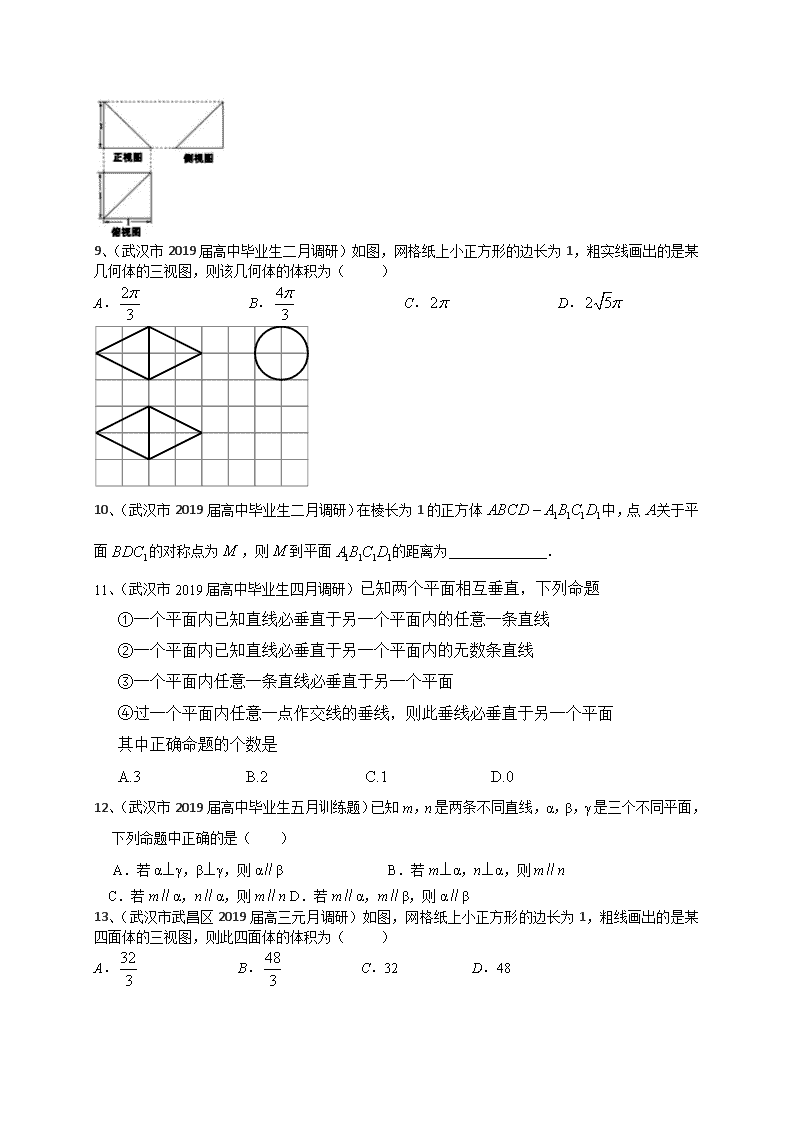D.‎ ‎6、（荆门市2019届高三元月调研）中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是 ‎ ‎7、（荆门市2019届高三元月调研）两个半径都是的球和球相切，且均与直二面角的两个半平面都相切，另有一个半径为的小球与这二面角的两个半平面也都相切，同时与球和球都外切，则的值为 A． B． C． D．‎ ‎8、（七市（州）教研协作体2019届高三3月联考）某几何体的三视图如图所示， 则该几何体的外接球的体积为 ‎　A、　　B、　　C、　　D、‎ ‎9、（武汉市2019届高中毕业生二月调研）如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为（ ）‎ A． B． C． D． ‎ ‎10、（武汉市2019届高中毕业生二月调研）在棱长为1的正方体中，点关于平面的对称点为，则到平面的距离为 ．‎ ‎11、（武汉市2019届高中毕业生四月调研）已知两个平面相互垂直，下列命题 ‎①一个平面内已知直线必垂直于另一个平面内的任意一条直线 ‎②一个平面内已知直线必垂直于另一个平面内的无数条直线 ‎③一个平面内任意一条直线必垂直于另一个平面 ‎④过一个平面内任意一点作交线的垂线，则此垂线必垂直于另一个平面 其中正确命题的个数是 A.3 B.2 C.1 D.0‎ ‎12、（武汉市2019届高中毕业生五月训练题）已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是（　　）‎ A．若α⊥γ，β⊥γ，则α∥β B．若m⊥α，n⊥α，则m∥n ‎ C．若m∥α，n∥α，则m∥n D．若m∥α，m∥β，则α∥β ‎13、（武汉市武昌区2019届高三元月调研）如图，网格纸上小正方形的边长为1，粗线画出的是某四面体的三视图，则此四面体的体积为（ ）‎ A． B． 　　　　　C．32 　　　　　D．48‎ ‎14、（湖北省重点高中联考协作体2019届高三上学期期中考试）将直角三角形沿斜边上的高折成的二面角，已知直角边，那么下面说法正确的是（ ）‎ A.平面平面 B.四面体的体积是 C.二面角的正切值是 D.与平面所成角的正弦值是 ‎15、（宜昌市（东湖高中、宜都二中）2019届高三12月联考）设，是两条不同的直线，是一个平面，则下列命题正确的是（ ）‎ A．若，，则 B．若，，则 C．若，，则 D．若，，则 ‎16、（武汉市2019届高中毕业生五月训练题）已知点P为半径等于2的球O球面上一点，过OP的中点E作垂直于OP的平面截球O的截面圆为圆E，圆E的内接△ABC中，∠ABC＝90°，点B在AC上的射影为D，则三棱锥P﹣ABD体积的最大值为　 　．‎ ‎17、（武汉市武昌区2019届高三元月调研）已知正三棱锥的所有顶点都在球的球面上，棱锥的底面是边长为的正三角形，侧棱长为，则球的表面积为（ ）‎ A． B． C． D． ‎ 参考答案：‎ ‎1、B 2、C 3、C 4、 5、C ‎6、A 7、D 8、C 9、B 10、‎ ‎11、C 12、B 13、A 14、C 15、D ‎16、解：如图，点P为半径等于2的球O球面上一点，‎ 过OP的中点E作垂直于OP的平面截球O的截面圆为圆E，‎ 圆E的内接△ABC中，∠ABC＝90°，点B在AC上的射影为D，‎ 由题意，PE＝OE＝1，‎ ‎∴AE＝CE＝，PA＝PB＝PC＝2，∠ABC＝90°，‎ 过B作BD⊥AC于D，设AD＝x，则CD＝2﹣x，‎ 再设BD＝y，由△BDC∽△ADB，可得＝，‎ ‎∴y＝，则＝，‎ 令f（x）＝﹣x4+2，则，‎ 由f′（x）＝0，可得x＝，‎ ‎∴当x＝时，f（x）max＝，‎ ‎∴△ABD面积的最大值为×＝，‎ 则三棱锥P﹣ABD体积的最大值是．‎ 故答案为：．‎ ‎17、B 二、解答题 ‎1、（荆、荆、襄、宜四地七校考试联盟2019届高三2月月考）在四棱锥P-ABCD中,底面ABCD是边长为的正方形,‎ 平面PAC⊥底面ABCD,PA=PC=. ‎ ‎（1）求证：PB=PD;‎ ‎（2）若点M,N分别是棱PA,PC的中点,平面DMN与棱PB的交点Q,‎ 则在线段BC上是否存在一点 H,使得DQ⊥PH,若存在,求BH的长,‎ 若不存在,请说明理由.‎ ‎2、（鄂州市2019届高三上学期期中考试）如图1，在直角中，，分别为的中点，连结并延长交于点，将沿折起，使平面平面，如图2所示．‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）求平面与平面所成锐二面角的余弦值．‎ ‎3、（华中师范大学第一附属中学2019届高三5月押题考）如图，在等腰梯形ABCD中，AB∥CD，AD=AB = BC =1，.CD=2，点E为CD中点，以AE为折痕把△ADE折起，使点D到达点P的位置(P平面ABCD).‎ ‎(1)证明:AE丄PB;‎ ‎(2)若直线PB与平面所成的角为，求二面角A-PE-C的余弦值.‎ ‎4、（黄冈、黄石等八市2019届高三3月联考）在如图所示的多面体中，平面ABB‎1A1⊥平面ABCD，四边形ABB‎1A1是 边长为2的菱形，四边形ABCD为直角梯形，四边形BCC1B1为平行四边形，且AB∥CD，AB⊥BC，CD＝1‎ ‎ （1）若E，F分别为A‎1C，BC1的中点，求证：EF⊥平面AB‎1C1；‎ ‎ （2）若∠A1AB＝60°，AC1与平面ABCD所成角的正弦值，求二面角A1-AC1-D的余弦值．‎ ‎ ‎ ‎5、（黄冈中学、华师一附中等八校2019届高三第二次（3月）联考）如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC=1，AD=2，CD=.‎ ‎ （Ⅰ）求证：平面PQB⊥平面PAD；‎ ‎（Ⅱ）若M是棱PC上的一点,且满足,求二面角M-BQ-C的大小.‎ ‎6、（黄冈中学、华师一附中等八校2019届高三第一次（12月）联考）如图所示，四棱锥中，，四边形为等腰梯形，,为的中点.‎ ‎（1）求证：.‎ ‎（2）求面与平面所成的二面角的正弦值.‎ ‎7、（荆门市2019届高三元月调研）如图（1），梯形中，，过、分别作，，垂足分别为．，已知，将梯形沿、同侧折起，得空间几何体，如图（2）．‎ ‎（Ⅰ）若，证明：⊥平面；‎ ‎（Ⅱ）若，，线段上存在一点，满足与平面所成角的正弦值为，求的长．‎ ‎8、（七市（州）教研协作体2019届高三3月联考）如图， 在四棱锥P - ABCD 中， ABCD 为平行四边形， AB ^ AC ， PA ^ 平面 ABCD，且 PA = AB = 3 ， AC = 2 ， 点 E 是 PD 的中点.‎ ‎（ 1） 求证： PB // 平面 AEC ；‎ ‎（ 2） 在线段 PB 上（ 不含端点） 是否存在一点 M ，使得二面角 M - AC - E 的余弦值为？ 若存在， 确定 M 的位置； 若不存在， 请说明理由.‎ ‎9、（武汉市2019届高中毕业生二月调研）如图，已知四边形为梯形，为矩形，平面平面，又．‎ ‎（1）证明：；‎ ‎（2）求二面角的余弦值．‎ ‎10、（武汉市2019届高中毕业生四月调研）如图，在四棱锥中，底面是平行四边形，，，，且平面平面.‎ ‎(1)求证：；‎ ‎(2)求二面角的余弦值. ‎ ‎11、（武汉市2019届高中毕业生五月训练题）如图l，直角梯形ABCD中，AB∥CD，AB⊥AD，AB＝2AD＝2DC＝6；如图2，将图l中△DAC沿AC折起，使得点D在面ABC上的正投影G在△ABC内部，点E为AB的中点，连接DB，DE，三棱锥D一ABC的体积为12．对于图2的几何体：‎ ‎（l）求证：DE⊥AC；‎ ‎（2）求DB与面DAC所成角的余弦值．‎ ‎12、（武汉市武昌区2019届高三元月调研）如图，三棱柱中，．‎ ‎（1）求证：平面平面；‎ ‎（2）求二面角的余弦值．‎ ‎13、（湖北省重点高中联考协作体2019届高三上学期期中考试）如图，在四棱锥中，平面，，且，.‎ ‎（1）求证：；‎ ‎（2）在线段上，是否存在一点，使得二面角的大小为，如果存在，求的值；如果不存在，请说明理 由.‎ ‎14、（荆门市第一中学2019届高三8月月考）如图，梯形中，，平面 平面.‎ ‎（1）求证：平面平面；‎ ‎（2）若，求与平面所成 ‎ 角的正弦值.‎ ‎15、（华师一附中、黄冈中学等八校2018届高三第二次联考）如图，四边形与均为菱形，，且．‎ ‎（1）求证：平面；‎ ‎（2）求直线与平面所成角的正弦值．‎ 参考答案：‎ ‎1、解：(1)证明：记AC∩BD=O，连结PO，‎ ‎∵底面ABCD为正方形，∴OA=OC=OB=OD=2.‎ ‎∵PA=PC，∴PO⊥AC，‎ ‎∵平面PAC∩底面ABCD=AC，POÌ平面PAC，‎ ‎∴PO⊥底面ABCD.‎ ‎∵BDÌ底面ABCD，∴PO⊥BD. ‎ ‎∴PB=PD. …………6分 ‎(2)以O为坐标原点，射线OB，OC，OP的方向分别为轴，轴，轴的正方向建立空间直角坐标系如图所示，由（1）可知OP=2.‎ 可得P(0,0,2)，A(0,-2,0), B(2,0,0), C(0,2,0), D(-2,0,0),‎ 可得，M(0,-1,1), N(0,1, 1).，.‎ 设平面的法向量n=，‎ ‎∵，，∴‎ 令，可得n=.‎ 记，可得，‎ ‎，=0，可得，，解得.‎ 可得，.‎ 记，可得，‎ ‎，若DQ⊥PH，则，‎ ‎，解得.故.…………12分 另：取的中点，说明均在平面PBD与平面DMN的交线上.‎ ‎2、（1）证明：由条件可知，而为的中点，，……………………2分 又面面，面面，且，平面……4分 又因为平面，． ……………………………………………………6分 ‎（2）由（1）可知，两两相互垂直，如图建立空间直角坐标系，则：‎ ‎……………………………7分 易知面的法向量为，………………………………………………………8分 设平面的法向量为，则：，易得…………………10分 设平面与平面所成锐二面角为，则………………12分 ‎3、‎ ‎4、【解析】（1）连接，∵四边形为菱形，∴．‎ ‎∵平面平面，平面平面，平面，，‎ ‎∴平面．又平面，∴．‎ ‎∵，∴．∵，∴平面．‎ ‎∵分别为，的中点，∴，∴平面．……5分 ‎（2）方法一：设，由（1）得平面，‎ 由，，得，．‎ 过点作，与的延长线交于点，取的中点，连接，，‎ 如图所示，‎ 又，∴为等边三角形，∴，‎ 又平面平面，平面平面，平面，‎ 故平面．‎ ‎∵为平行四边形，∴，∴平面．‎ 又∵，∴平面．‎ ‎∵，∴平面平面．‎ 由（1），得平面，∴平面，∴．‎ ‎∵，∴平面，∴是与平面所成角．‎ ‎∵，，∴平面，平面，∵，‎ ‎∴平面平面．‎ ‎∴，，解得．……8分 在梯形中，易证，‎ 分别以，，的正方向为轴，轴，轴的正方向建立空间直角坐标系．‎ 则，，，，，，‎ 由，及，得，‎ ‎∴，，．‎ 设平面的一个法向量为，由得，‎ 令，得 设平面的一个法向量为，由得，‎ 令，得．∴，‎ 又∵二面角是钝角，∴二面角的余弦值是．……12分 ‎（2）方法二：以AB中点为原点建立如图空间直角坐标系，设BC=t,‎ 则，，，，‎ 平面ABCD的法向量n=(0,0,1), 解得，∴，，．下同解法一 ‎5、‎ ‎6、（1）‎ ‎∵∴ 又∵‎ ‎∴∴‎ ‎∵‎ ‎∴ ………………4分 又∵ ∴ ………………6分 ‎（2），， ‎ ‎ ,‎ ‎， ………………8分 ‎∴………………12分 ‎7、解：（Ⅰ）证明：由已知得四边形ABFE是正方形，且边长为2，在图2中，AF⊥BE，‎ 由已知得AF⊥BD，BE∩BD=B，∴AF⊥平面BDE………………………………2分 又DE⊂平面BDE，∴AF⊥DE，‎ 又AE⊥DE，AE∩AF=A，∴DE⊥平面ABFE，……………………………………5分 ‎（Ⅱ）在图2中，AE⊥DE，AE⊥EF，DE∩EF=E，即AE⊥面DEFC，‎ 在梯形中，过点作//交于点，连接，‎ 易得，，则DC⊥CF，则， ，‎ 过E作EG⊥EF交DC于点G，可知GE，EA，EF两两垂直，以E为坐标原点，以 分别为x轴，y轴，z轴的正方向建立空间直角坐标系，………………7分 则 设平面ACD的一个法向量为，‎ 由得取得 设，则，得 设CP与平面ACD所成的角为 所以．…………………………………………12分 ‎8、解： (1)连接 BD 交 AC 于 F 点， 连接 EF ，‎ 在 DPBD 中， EF // PB ， ……………………………………2 分 又 EF Ì 面AEC，PB Ë 面AEC PB //面AEC . ………………………………………4 分 ‎（ 2）由题意知， AC，AB，AP 两两互相垂直，如图以 A 为坐标原点，建立空间直角坐标 系，‎ 射线 AC，AB，AP 分别为 x，y，z 轴建立空间直角坐标系O - xyz .‎ ‎9、解法一：（1）为矩形，且平面平面，‎ 平面平面，在中，，‎ 在梯形中，，从而．‎ 在中，，可知，‎ 在中，，可知，‎ 又，‎ 平面，又平面．……………………………………6分 ‎（2）取的中点，连接，由知，‎ 由知，为二面角的平面角．‎ 由（1）知平面，，又，‎ ‎，．‎ 解法二：（1）为矩形，且平面平面，平面，又，所以可以以为原点建立如图所示空间直角坐标系，则 ‎，‎ ‎．‎ ‎（2），‎ 设平面的法向量为，则 ，令，得．‎ 设平面的法向量为，则，令，得．‎ ‎，‎ 因为二面角为锐角，所以二面角的余弦值为．‎ ‎10、【解答】‎ ‎(2)解析2：面，设二面角的平面角为，‎ ‎ ，，到距离为，‎ ‎ 二面角的平面角为，‎ ‎11、证明：（1）在直角梯形ABCD中，AB∥CD，AB⊥CD，AB＝2AD＝2DC＝6，‎ 在图1中作AB的中点E，在图1、图2中，取AC的中点F，‎ 连结DF、CE、EF，则△DAC，△EAC均为等腰直角三角形，‎ AC⊥DF，AC⊥EF，又DF∩EF＝F，∴AC⊥面DEF，‎ 又DE⊂面DEF，∴DE⊥AC．‎ 解：（2）∵DG⊥面ABC，∴DG⊥AG，DG⊥GC，‎ ‎∵DA＝DC，∴GA＝GC，∴G在AC的中垂线上，‎ ‎∴EG垂直平分AC，‎ 又F为AC中点，∴E，F，G共线，‎ ‎∵AB＝2AD＝2DC＝6，∴△ABC是等腰直角三角形，‎ ‎＝＝18，‎ ‎＝＝12，‎ 解得DG＝2，‎ 在等腰直角△DAC和等腰直角△EAC中，‎ EF＝DF＝＝3，‎ 在Rt△DGF中，GF＝＝＝1，‎ 以G为原点，过G为z轴，GM、GE、GD所在直线分别为x，y，z轴，建立空间直角坐标系，‎ 则A（3，﹣1，0），B（﹣3，5，0），C（﹣3，﹣1，0），D（0，0，2），‎ 则＝（﹣3，5，﹣2），＝（3，﹣1，﹣2），＝（﹣3，﹣1，﹣2），‎ 设面DAC的法向量＝（x，y，z），‎ 则，令z＝1，则＝（0，﹣2，1），‎ cos＜＞＝＝﹣，‎ ‎∴DB与面DAC所成角的余弦值为＝．‎ ‎12、解析：（1）记，连结．因为，所以．‎ 由题意知为正三角形，求得，在中求得，又，‎ 所以，所以．因为，所以平面．‎ 因为平面，所以平面平面．………………………………6分 ‎（2）建立如图所示的空间直角坐标系，则，‎ ‎．‎ 因为平面，所以平面的法向量为．‎ 设平面的法向量为，则，取，则，‎ 所以．‎ 所以，因为所求二面角的平面角为钝角，‎ 所以所求二面角的余弦值为．………………………………………………12分 ‎13、【解析】(1)证明：如图，由已知得四边形是直角梯形，‎ 由已知，‎ 可得是等腰直角三角形，即，‎ 又平面，则，‎ 又,所以平面，‎ 所以; ‎ ‎（2）建立如图所示空间直角坐标系，则 设，则的坐标为设是平面的一个法向量，则 ‎，得，则可取 又是平面的一个法向量，‎ 所以，‎ ‎ ‎ ‎14、【解析】（1）证明：∵平面⊥平面，平面∩平面=，平面，，∴⊥平面. 又平面,∴平面⊥平面. ‎ ‎（2）设，∵四边形为等腰梯形，⊥，=2=，‎ ‎∴ ，，∵且，∴四边形为平行四边形，‎ ‎∴，且，又∵⊥平面，∴⊥平面. ‎ 以为原点，向量的方向分别为x轴，y轴， z轴的正方向，建立如图所示的空间直角坐标系， 则，，，，，，， ‎ 设平面DFC的一个法向量为，‎ 有，即，不妨设，得.取， ‎ 于是. 设与平面所成角为，则．‎ ‎∴与平面所成角的正弦值为．‎ ‎15、解析：（1）设与相交于点，连接，‎ ‎∵四边形为菱形，∴，且为中点，‎ ‎∵，∴,‎ 又，∴平面.…………………5分 ‎（2）连接，∵四边形为菱形，且，∴为等边三角形，‎ ‎∵为中点，∴，又，∴平面.‎ ‎∵两两垂直，∴建立空间直角坐标系，如图所示，………7分 设，∵四边形为菱形， ，∴. ‎ ‎∵为等边三角形，∴.‎ ‎∴，‎ ‎∴.‎ 设平面的法向量为，则，‎ 取，得.设直线与平面所成角为，………10分 则. …………………12分 注：用等体积法求线面角也可酌情给分