【数学】2020届一轮复习（文）通用版14数系的扩充与复数的引入作业 9页

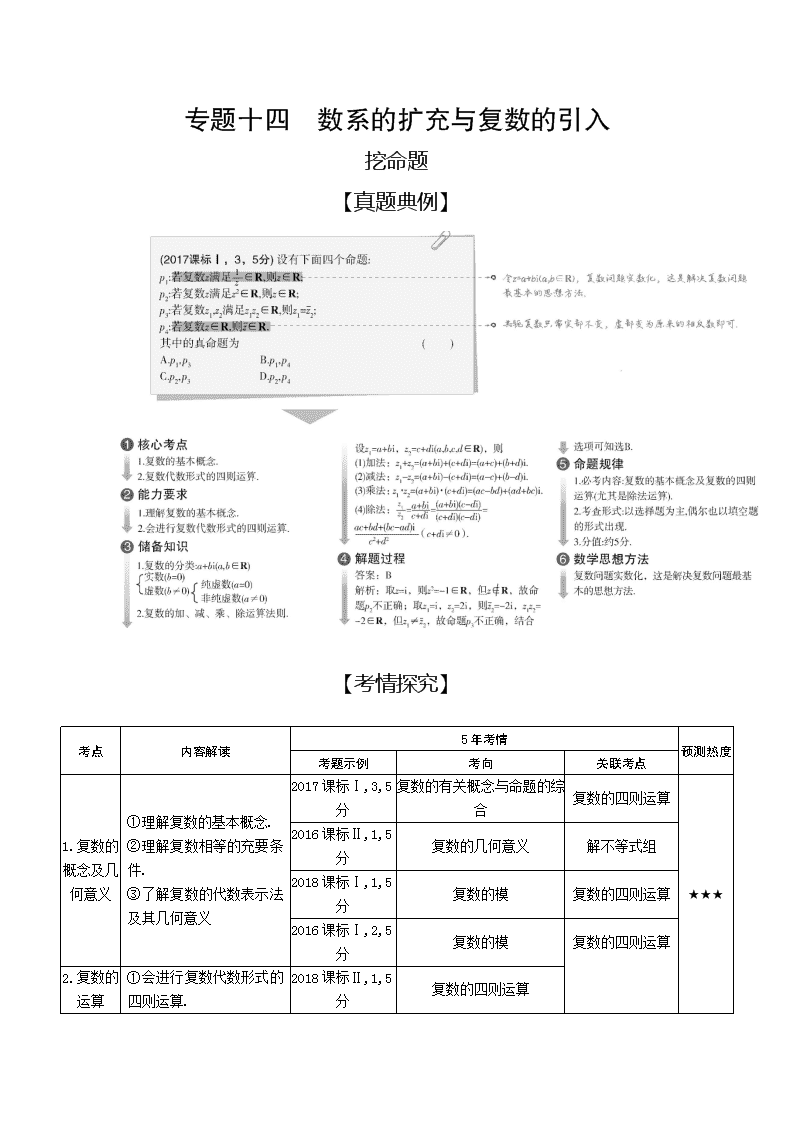
专题十四　数系的扩充与复数的引入 挖命题 ‎【真题典例】‎ ‎【考情探究】‎ 考点 内容解读 ‎5年考情 预测热度 考题示例 考向 关联考点 ‎1.复数的 概念及几 何意义 ‎①理解复数的基本概念.‎ ‎②理解复数相等的充要条件.‎ ‎③了解复数的代数表示法及其几何意义 ‎2017课标Ⅰ,3,5分 复数的有关概念与命题的综合 复数的四则运算 ‎★★★‎ ‎2016课标Ⅱ,1,5分 复数的几何意义 解不等式组 ‎2018课标Ⅰ,1,5分 复数的模 复数的四则运算 ‎2016课标Ⅰ,2,5分 复数的模 复数的四则运算 ‎2.复数的 运算 ‎①会进行复数代数形式的四则运算.‎ ‎2018课标Ⅱ,1,5分 复数的四则运算 ‎②了解复数代数形式的加、减运算的几何意义 ‎2018课标Ⅲ,2,5分 ‎2016课标Ⅲ,2,5分 ‎2014课标Ⅰ,2,5分 分析解读　　本专题是高考的热点,主要考查复数的有关概念和复数的四则运算,一般出现在选择题的前3题中,比较简单,属于送分题,分值为5分.主要考查考生的数学运算能力和等价转化思想的应用.‎ 破考点 ‎【考点集训】‎ 考点一　复数的概念及几何意义　　　　　　　 　　　　　　 　　　　　　 ‎ ‎1.(2018江西重点中学盟校第一次联考,2)设x∈R,i是虚数单位,则“x=2”是“复数z=(x2-4)+(x+2)i为纯虚数”的(　　)‎ A.充分不必要条件　　　　‎ B.充要条件 C.必要不充分条件　　　　‎ D.既不充分也不必要条件 答案　B　‎ ‎2.(2017安徽江淮十校第三次联考,1)在复平面内,复数z=cos 3+isin 3(i为虚数单位),则|z|为(　　)‎ A.1　　　　B.2　　　　C.3　　　　D.4‎ 答案　A　‎ 考点二　复数的运算 ‎1.(2018河南豫南九校第六次质量考评,2)已知复数a+i‎2+i=x+yi(a,x,y∈R,i是虚数单位),则x+2y=(　　)‎ A.1　　　　B.‎3‎‎5‎　　　　C.-‎3‎‎5‎　　　　D.-1‎ 答案　A　‎ ‎2.(2018河北邯郸一模,1)已知复数z=-1+i(i是虚数单位),则z+2‎z‎2‎‎+z=(　　)‎ A.-1　　　　B.1　　　　C.-i　　　　D.i 答案　A　‎ ‎3.(2018江西赣州模拟,2)若z=2+i,则‎4iz·z-1‎=(　　)‎ A.i　　　　B.-i　　　　C.1　　　　D.-1‎ 答案　A　‎ 炼技法 ‎【方法集训】‎ 方法1　复数概念的解题方法 ‎　　　　　　 　　　　　　 　　　　　　 ‎ ‎1.(2018江西吉安一中、九江一中等八所重点中学4月联考,2)在复平面内,复数z对应的点与‎2‎‎1-i对应的点关于实轴对称,则z等于(　　)‎ A.1+i　　　　B.-1-i　　　　‎ C.-1+i　　　　D.1-i 答案　D　‎ ‎2.(2018安徽安庆二模,1)已知复数a+i‎2-i是纯虚数(i是虚数单位),则实数a等于(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.-2　　　　B.2　　　　C.‎1‎‎2‎　　　　D.-1‎ 答案　C　‎ ‎3.(2017浙江,12,6分)已知a,b∈R,(a+bi)2=3+4i(i是虚数单位),则a2+b2=　　　　,ab=　　　　. ‎ 答案　5;2‎ 方法2　复数的四则运算解题方法 ‎1.(2018湖南师大附中月考,1)设i是虚数单位,则-1+i-i2+i3-i4+…-i100=(　　)‎ A.1　　　　B.0　　　　C.-1　　　　D.i 答案　C　‎ ‎2.(2017广东汕头第三次质检,1)已知i为虚数单位,则‎1-i‎1+i‎2‎=(　　)‎ A.-1　　　　B.1　　　　C.-i　　　　D.i 答案　A　‎ 过专题 ‎【五年高考】‎ A组　统一命题·课标卷题组 考点一　复数的概念及几何意义 ‎1.(2017课标Ⅲ,2,5分)设复数z满足(1+i)z=2i,则|z|=(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.‎1‎‎2‎　　　　B.‎2‎‎2‎　　　　C.‎2‎　　　　D.2‎ 答案　C　‎ ‎2.(2016课标Ⅱ,1,5分)已知z=(m+3)+(m-1)i在复平面内对应的点在第四象限,则实数m的取值范围是(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A.(-3,1)　　　　B.(-1,3)‎ C.(1,+∞)　　　　D.(-∞,-3)‎ 答案　A　‎ ‎3.(2015课标Ⅱ,2,5分)若a为实数,且(2+ai)(a-2i)=-4i,则a=(　　)‎ A.-1　　　　B.0　　　　C.1　　　　D.2‎ 答案　B　‎ 考点二　复数的运算 ‎1.(2018课标Ⅲ,2,5分)(1+i)(2-i)=(　　)‎ A.-3-i　　　　B.-3+i　　　　C.3-i　　　　D.3+i 答案　D　‎ ‎2.(2016课标Ⅲ,2,5分)若z=1+2i,则‎4izz-1‎=(　　)‎ A.1　　　　B.-1　　　　C.i　　　　D.-i 答案　C　‎ ‎3.(2014课标Ⅰ,2,5分)‎(1+i‎)‎‎3‎‎(1-i‎)‎‎2‎=(　　)‎ A.1+i　　　　B.1-i　　　　C.-1+i　　　　D.-1-i 答案　D　‎ B组　自主命题·省(区、市)卷题组 考点一　复数的概念及几何意义 ‎1.(2018浙江,4,4分)复数‎2‎‎1-i(i为虚数单位)的共轭复数是(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.1+i　　　　B.1-i　　　　C.-1+i　　　　D.-1-i 答案　B　‎ ‎2.(2017北京,2,5分)若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是(　　)‎ A.(-∞,1)　　　　B.(-∞,-1)　　　　C.(1,+∞)　　　　D.(-1,+∞)‎ 答案　B　‎ ‎3.(2018江苏,2,5分)若复数z满足i·z=1+2i,其中i是虚数单位,则z的实部为　　　　. ‎ 答案　2‎ 考点二　复数的运算 ‎1.(2015湖北,1,5分)i为虚数单位,i607的共轭复数‎····‎为(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.i　　　　B.-i　　　　C.1　　　　D.-1‎ 答案　A　‎ ‎2.(2018天津,9,5分)i是虚数单位,复数‎6+7i‎1+2i=　　　　. ‎ 答案　4-i C组　教师专用题组 考点一　复数的概念及几何意义　　　　　　　 　　　　　　 　　　　　　 ‎ ‎1.(2014重庆,1,5分)复平面内表示复数i(1-2i)的点位于(　　)‎ A.第一象限　　　　B.第二象限　　　　C.第三象限　　　　D.第四象限 答案　A　‎ ‎2.(2016山东,1,5分)若复数z满足2z+z=3-2i,其中i为虚数单位,则z=(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.1+2i　　　　B.1-2i　　　　C.-1+2i　　　　D.-1-2i 答案　B　‎ ‎3.(2015广东,2,5分)若复数z=i(3-2i)(i是虚数单位),则z=　(　　)‎ A.2-3i　　　　B.2+3i C.3+2i　　　　D.3-2i 答案　A　‎ ‎4.(2015湖南,1,5分)已知‎(1-i‎)‎‎2‎z=1+i(i为虚数单位),则复数z=(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.1+i　　　　B.1-i　　　　C.-1+i　　　　D.-1-i 答案　D　‎ ‎5.(2015山东,2,5分)若复数z满足z‎1-i=i,其中i为虚数单位,则z=(　　)‎ A.1-i　　　　B.1+i　　　　C.-1-i　　　　D.-1+i 答案　A　‎ ‎6.(2014课标Ⅱ,2,5分)设复数z1,z2在复平面内的对应点关于虚轴对称,z1=2+i,则z1z2=(　　)‎ A.-5　　　　B.5　　　　C.-4+i　　　　D.-4-i 答案　A　‎ ‎7.(2016课标Ⅰ,2,5分)设(1+i)x=1+yi,其中x,y是实数,则|x+yi|=(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A.1　　　　B.‎2‎　　　　C.‎3‎　　　　D.2‎ 答案　B　‎ ‎8.(2015课标Ⅰ,1,5分)设复数z满足‎1+z‎1-z=i,则|z|=(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.1　　　　B.‎2‎　　　　C.‎3‎　　　　D.2‎ 答案　A　‎ ‎9.(2017江苏,2,5分)已知复数z=(1+i)(1+2i),其中i是虚数单位,则z的模是　　　　. ‎ 答案　‎‎10‎ 解析　∵z=(1+i)(1+2i)=1+2i+i+2i2=3i-1,‎ ‎∴|z|=‎3‎‎2‎‎+(-1‎‎)‎‎2‎=‎10‎.‎ ‎10.(2016北京,9,5分)设a∈R.若复数(1+i)(a+i)在复平面内对应的点位于实轴上,则a=　　　　. ‎ 答案　-1‎ ‎11.(2016江苏,2,5分)复数z=(1+2i)(3-i),其中i为虚数单位,则z的实部是　　　　. ‎ 答案　5‎ ‎12.(2015重庆,11,5分)设复数a+bi(a,b∈R)的模为‎3‎,则(a+bi)(a-bi)=　　　　. ‎ 答案　3‎ ‎13.(2015天津,9,5分)i是虚数单位,若复数(1-2i)(a+i)是纯虚数,则实数a 的值为　　　　. ‎ 答案　-2‎ 考点二　复数的运算 ‎1.(2017山东,2,5分)已知a∈R,i是虚数单位.若z=a+‎3‎i,z·z=4,则a=(　　)‎ A.1或-1　　　　B.‎7‎或-‎‎7‎ C.-‎3‎　　　　D.‎‎3‎ 答案　A　‎ ‎2.(2017课标Ⅱ,1,5分)‎3+i‎1+i=(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.1+2i　　　　B.1-2i　　　　C.2+i　　　　D.2-i 答案　D　‎ ‎3.(2015北京,1,5分)复数i(2-i)=(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.1+2i　　　　B.1-2i　　　　C.-1+2i　　　　D.-1-2i 答案　A　‎ ‎4.(2014安徽,1,5分)设i是虚数单位,z表示复数z的共轭复数.若z=1+i,则zi+i·z=(　　)‎ A.-2　　　　B.-2i　　　　C.2　　　　D.2i 答案　C　‎ ‎5.(2014山东,1,5分)已知a,b∈R,i是虚数单位,若a-i与2+bi互为共轭复数,则(a+bi)2=(　　)‎ A.5-4i　　　　B.5+4i　　　　C.3-4i　　　　D.3+4i 答案　D　‎ ‎6.(2014湖南,1,5分)满足z+iz=i(i为虚数单位)的复数z=(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.‎1‎‎2‎+‎1‎‎2‎i　　　　B.‎1‎‎2‎-‎1‎‎2‎i　　　　C.-‎1‎‎2‎+‎1‎‎2‎i　　　　D.-‎1‎‎2‎-‎1‎‎2‎i 答案　B　‎ ‎7.(2016天津,9,5分)已知a,b∈R,i是虚数单位.若(1+i)(1-bi)=a,则ab的值为　　　　. ‎ 答案　2‎ ‎8.(2015江苏,3,5分)设复数z满足z2=3+4i(i是虚数单位),则z的模为　　　　. ‎ 答案　‎‎5‎ ‎9.(2014上海,2,4分)若复数z=1+2i,其中i是虚数单位,则z+‎‎1‎z·z=　　　　. ‎ 答案　6‎ ‎【三年模拟】‎ 选择题(每小题5分,共55分)‎ ‎1.(2019届河南名校联盟高三“尖子生”调研考试,2)已知i为虚数单位,则‎2-4i‎1+3i=(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.-1-i　　　　B.-1+i　　　　C.1-i　　　　D.1+i 答案　A　‎ ‎2.(2019届沈阳东北育才学校高三联合考试,8)欧拉公式eix=cos x+isin x(i为虚数单位)是瑞士数学家欧拉发明的,将指数的定义域扩大到复数集,建立了三角函数和指数函数的联系,被誉为“数学中的天桥” .根据欧拉公式可知,eπ‎6‎i+eπ‎3‎i表示的复数的模为(　　)‎ A.‎3‎‎+1‎‎2‎　　　　B.‎3‎‎-1‎‎2‎　　　　C.‎6‎‎+‎‎2‎‎2‎　　　　D.‎‎6‎‎-‎‎2‎‎2‎ 答案　C　‎ ‎3.(2019届广东汕头达濠华侨中学、东厦中学第三次联考,2)已知i为虚数单位,则复数z=‎|‎3‎-i|‎‎1+i的共轭复数z为(　　)‎ A.2+2i　　　　B.2-2i　　　　C.1+i　　　　D.1-i 答案　C　‎ ‎4.(2019届陕西四校联考高三模拟,2)已知复数z=‎3‎‎1-2i(i是虚数单位),则z的实部为(　　)‎ A.-‎3‎‎5‎　　　　B.‎3‎‎5‎　　　　C.-‎1‎‎5‎　　　　D.‎‎1‎‎5‎ 答案　B　‎ ‎5.(2018四川德阳三校联考,2)若(x+2i)i=y-‎1‎i(x,y∈R),则x+y=(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.-1　　　　B.1　　　　C.3　　　　D.-3‎ 答案　A　‎ ‎6.(2018江西上饶第二次模拟,2)设a,b∈R,a=‎3+bi‎3-2i(i是虚数单位),则b=(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.-2　　　　B.-1　　　　C.1　　　　D.2‎ 答案　A　‎ ‎7.(2017安徽黄山二模,2)复数z=(a+1)+(a2-3)i(i为虚数单位),若z<0,则实数a的值是(　　)‎ A.‎3‎　　　　B.1　　　　C.-1　　　　D.-‎‎3‎ 答案　D　‎ ‎8.(2018江西八所重点中学联考,2)设复数z满足z=‎|2+i|+2ii(i为虚数单位),则|z|=(　　)‎ A.3　　　　B.‎10‎　　　　C.9　　　　D.10‎ 答案　A　‎ ‎9.(2018湖南G10教育联盟4月联考,2)已知复数z=‎3‎‎1-2i(i是虚数单位),则 z=(　　)‎ A.‎3‎‎5‎-‎6‎‎5‎i　　　　B.‎3‎‎5‎+‎6‎‎5‎I ‎1‎‎5‎-‎2‎‎5‎i　　　　D.‎1‎‎5‎+‎2‎‎5‎i 答案　A　‎ ‎10.(2018湖南三湘名校教育联盟第三次联考,2)已知i为虚数单位,复数z=‎3+2i‎2-i,则以下为真命题的是(　　)‎ A.z的共轭复数为‎7‎‎5‎-‎‎4i‎5‎ B.z的虚部为‎8‎‎5‎ C.|z|=3‎ D.z在复平面内对应的点在第一象限 答案　D　‎ ‎11.(2017河南百校联盟4月模拟,2)已知复数z的共轭复数为z,若‎3z‎2‎‎+‎z‎2‎(1-2‎2‎i)=5-‎2‎i(i为虚数单位),则在复平面内,复数z所对应的点位于(　　)‎ A.第一象限　　　　B.第二象限 C.第三象限　　　　D.第四象限 答案　A　‎