山西省太原五中2020届高三上学期阶段性检测（9月）数学（理）试卷答案 7页

太原五中2019—2020学年度第一学期阶段性检测 高 三 数 学(理)‎ 高三数学答案（理）‎ 一、选择题 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答 案 B B B A D A B C A A D A 二、填空题 题 号 ‎13‎ ‎14‎ ‎15‎ ‎16‎ 答 案 ‎9‎ ‎(-∞, -5)‎ ‎12‎ 三、解答题 ‎17.(1)证明：f(x+y)=f(x)+f(y) (x，y∈R)， ①‎ 令x=y=0，代入①式，得f(0+0)=f(0)+f(0)，即 f(0)=0．‎ 令y=-x，代入①式，得 f(x-x)=f(x)+f(-x)，又f(0)=0，‎ 则有0=f(x)+f(-x)．即f(-x)=-f(x)对任意x∈R成立，‎ 所以f(x)是奇函数．‎ ‎ (2)解：＞0，即f(3)＞f(0)，又在R上是单调函数，‎ 所以在R上是增函数 ‎ 又由(1)f(x)是奇函数．f(k·3)＜-f(3-9-2)=f(-3+9+2)， ‎ ‎∴ k·3＜-3+9+2，3-(1+k)·3+2＞0对任意x∈R成立． ‎ 令t=3＞0，问题等价于t-(1+k)t+2＞0‎ 对任意t＞0恒成立．‎ R恒成立．‎ ‎18.（Ⅰ）f(x)的单调递减区间是(－∞，ln2)，单调递增区间是(ln2，＋∞),极小值为f(ln2)＝eln2－2ln2＋2a＝2(1－ln2＋a)；‎ ‎19. 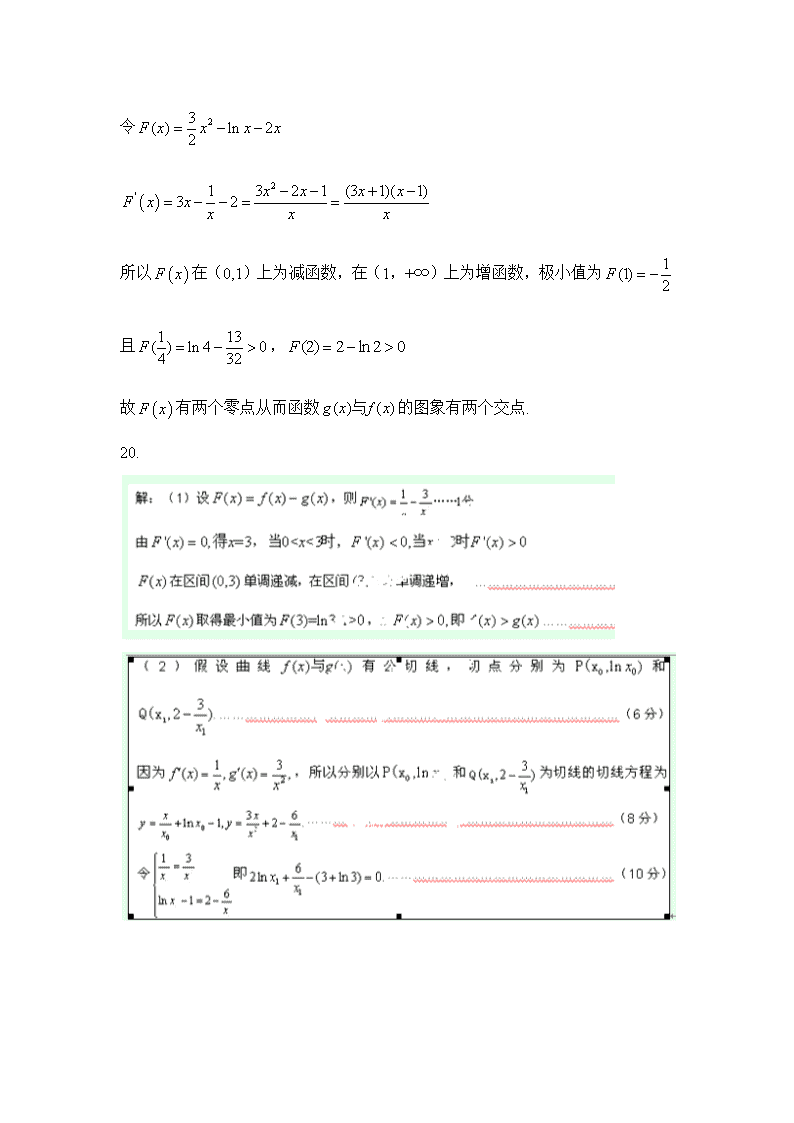解析：由题意得f′(x)＝2x＋－(2＋a)＝＝，x∈(0，＋∞)．‎ ‎(1))①当a≤0时，函数f(x)在(0,1)上单调递减，在(1，＋∞)上单调递增．‎ ‎②当a>0时，令f′(x)＝0得x＝1或x＝，‎ 当＝1，即a＝2时，在(0，＋∞)上恒有f′(x)≥0，故函数f(x)在(0，＋∞)上单调递增．‎ 当<1，即01，即a>2时，函数f(x)在(0,1)，上单调递增，在上单调递减；‎ ‎ (2) 即，‎ 化简得 令 ‎ 所以在（0,1）上为减函数，在（1，+∞）上为增函数，极小值为 且，‎ 故有两个零点从而函数的图象有两个交点.‎ ‎20.‎ ‎21.解：（Ⅰ）∵，∴. ……………………………1分 ‎∵切线与直线平行，‎ ‎∴，∴. ……………………………………………2分 ‎（Ⅱ）易得()，‎ ‎ ∴ ().‎ 由题意，知函数存在单调递减区间,等价于在上有解，‎ ‎∵，则故可设.…………………………………4分 而，所以，要使在上有解，‎ 则只须， 即，‎ 故所求实数的取值范围是. ……………………………………………5分 ‎（Ⅲ）由（Ⅱ）知，，‎ 令，得.‎ ‎∵()是函数的两个极值点，‎ ‎∴()是方程的两个根，‎ ‎∴，. …………………………………………………7分 ‎ ∴‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ …………………………………………8分 令，∵，∴，‎ 且.‎ ‎∵，∴，‎ ‎∴‎ ‎ ‎ 化简整理，得,解得或.‎ 而，∴. ……………………………………………………10分 ‎ 又，∴函数在单调递减，‎ ‎ ∴. …………………………………………………11分 ‎ 故的最小值为. ………………………………………12分 ‎ ‎22．【解析】（1）由，得，‎ 由，得，‎ 因为，消去得，所以直线的直角坐标方程为，‎ 曲线的普通方程为．‎ ‎（2）点的直角坐标为，点在直线上，‎ 设直线的参数方程为（为参数），代入，‎ 得，‎ 设点对应的参数分别为，则，，‎ 所以．‎ ‎23．【解析】（1），即，‎ 不等式等价于或或，‎ 解得或，‎ 所以的解集为．‎ ‎（2）因为，使得成立，‎ 所以，‎ 又，所以，‎ 当，即时，，解得，所以；‎ 当，即时，，解得，所以；‎ 当，即时，‎ 解得或，所以或，‎ 综上，实数的取值范围为．‎