广东省珠海市202-2013学年高一数学下学期期末考试试题（A卷）新人教A版 11页

珠海市2012～2013学年度第二学期期末学生学业质量监测 高一数学试题（A卷）及参考答案 时量：120分钟 分值：150分 ．适用学校：全市各高中使用A卷学校．‎ 内容：数学必修②第二章，数学必修③，数学必修④．‎ 一、选择题（本大题共12小题，每小题5分，共60分，每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1.(平面向量) 已知平面向量，，且与平行，则（ ）‎ A． B． C． D．‎ ‎2.(三角函数) 的值是（ ）A． B． C． D．‎ ‎3.(概率) 一个人打靶时连续射击两次,事件“至少有一次中靶”的对立事件是(　　 ).‎ A. 至多有一次中靶 B. 两次都中靶 C. 只有一次中靶 D. 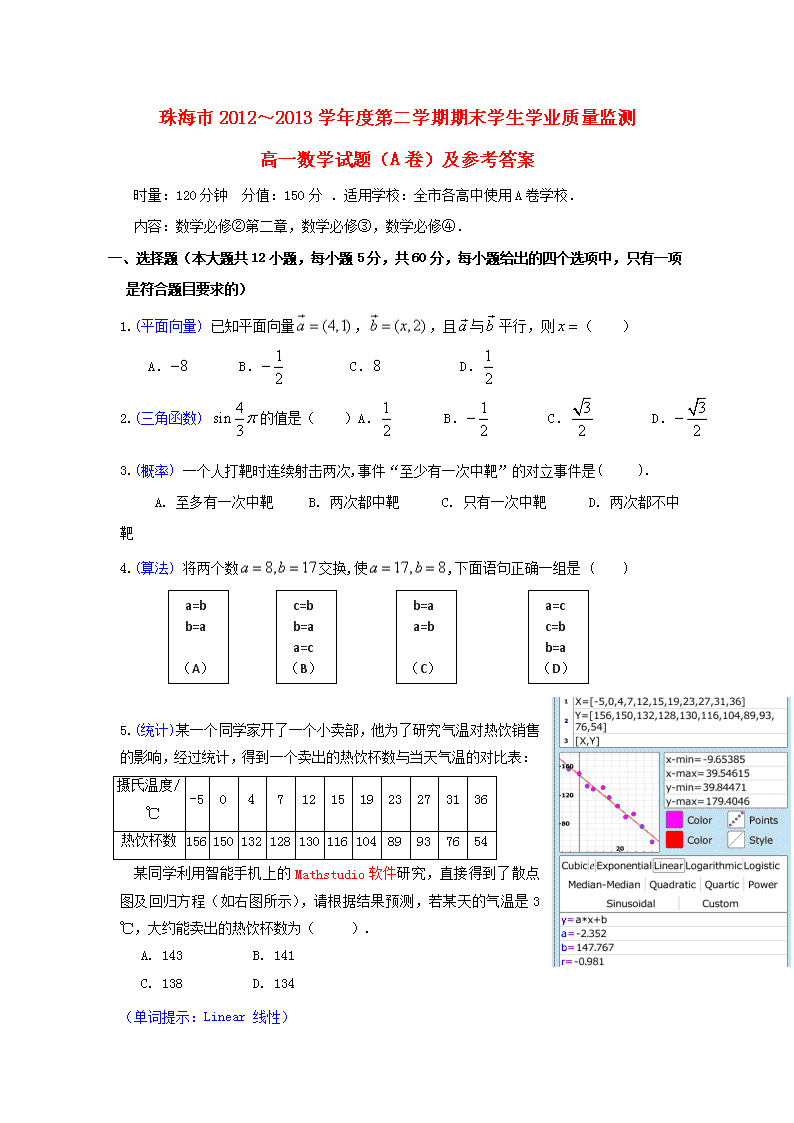两次都不中靶 ‎4.(算法) 将两个数交换,使,下面语句正确一组是 ( )‎ a=c c=b b=a ‎（D） ‎ c=b b=a a=c ‎（B）‎ b=a a=b ‎（C）‎ a=b b=a ‎（A）‎ ‎ ‎ ‎5.(统计)某一个同学家开了一个小卖部，他为了研究气温对热饮销售的影响，经过统计，得到一个卖出的热饮杯数与当天气温的对比表：‎ 摄氏温度/℃‎ ‎-5‎ ‎0‎ ‎4‎ ‎7‎ ‎12‎ ‎15‎ ‎19‎ ‎23‎ ‎27‎ ‎31‎ ‎36‎ 热饮杯数 ‎156‎ ‎150‎ ‎132‎ ‎128‎ ‎130‎ ‎116‎ ‎104‎ ‎89‎ ‎93‎ ‎76‎ ‎54‎ ‎ 某同学利用智能手机上的Mathstudio软件研究，直接得到了散点图及回归方程（如右图所示），请根据结果预测，若某天的气温是‎3℃‎，大约能卖出的热饮杯数为（ ）.‎ ‎ A. 143 B. 141‎ ‎ C. 138 D. 134‎ ‎（单词提示：Linear 线性）‎ ‎6.(统计) 要从已编号（）的枚最新研制的某型导弹中随机抽取枚来进行发射试验，用每部分选取的号码间隔一样的系统抽样方法确定所选取的枚导弹的编号可能是（　　）‎ A． B． C． D．‎ ‎7.(平面向量) 如右下图所示，是的边上的中点，记，，则向量（ ）‎ A． B． C． D．‎ n=5‎ s=0‎ WHILE s<15‎ ‎ s = s + n ‎ n=n－1‎ WEND PRINT n END ‎(第9题)‎ ‎8.(平面向量) 若,，且与的夹角为，则（ ）‎ A． B． C． D． ‎ ‎9.(算法) 右边程序执行后输出的结果是（ ）‎ A. B． C． D．‎ ‎10.(圆一般方程) 直线与圆相切，则的值为（ ）A． B．或 C． D．或 ‎11.(三角函数)将函数的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得的图象向左平移个单位，得到的图象对应的解析式是（ ）‎ A． B． C. 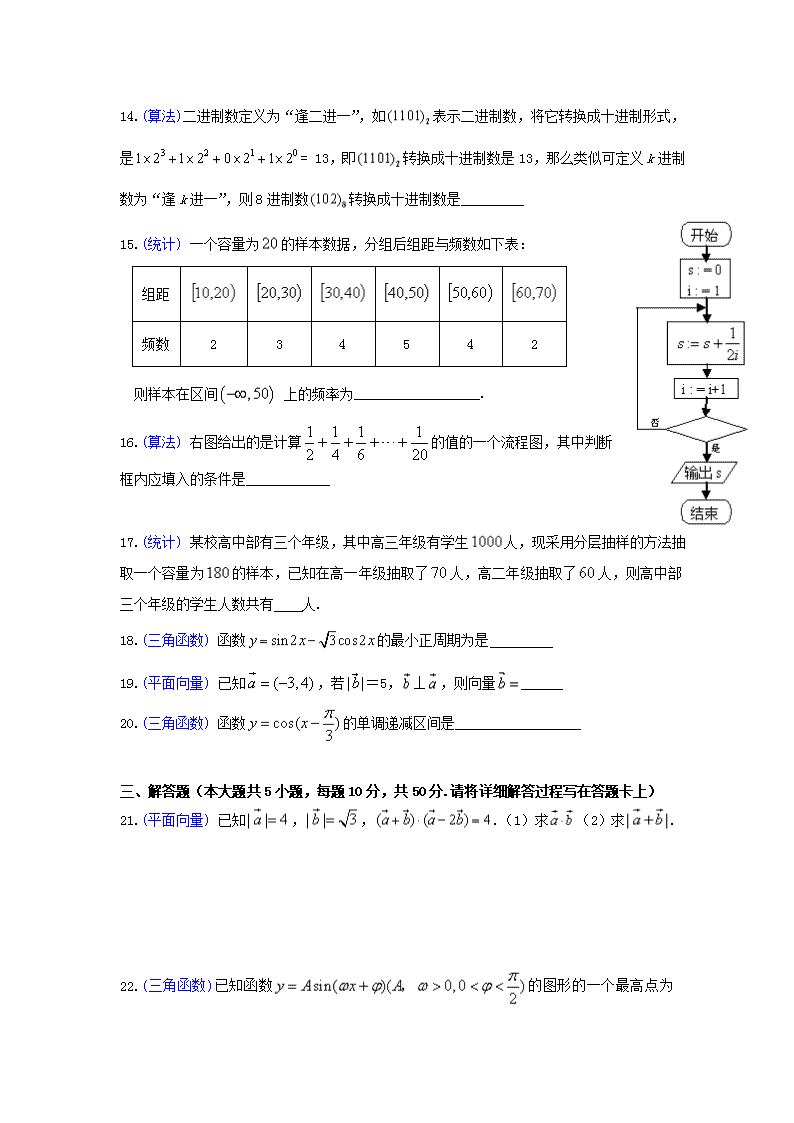D.‎ ‎12.(三角变换) 已知，，则（ ）‎ A． B． C． D． ‎ 二、填空题（本大题共8小题，每小题5分，共40分,请将正确答案填在答题卡上）‎ ‎13.(圆的方程) 以为直径两端点的圆的标准方程为 ． ‎ ‎14.(算法)二进制数定义为“逢二进一”，如表示二进制数，将它转换成十进制形式，是= 13，即转换成十进制数是13，那么类似可定义k进制数为“逢k进一”，则8进制数转换成十进制数是_________‎ ‎15.(统计) 一个容量为的样本数据，分组后组距与频数如下表：‎ 组距 频数 ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎4‎ ‎2‎ 则样本在区间 上的频率为__________________.‎ ‎16.(算法) 右图给出的是计算的值的一个流程图，其中判断 框内应填入的条件是____________‎ ‎17.(统计) 某校高中部有三个年级，其中高三年级有学生人，现采用分层抽样的方法抽取一个容量为的样本，已知在高一年级抽取了人，高二年级抽取了人，则高中部三个年级的学生人数共有 人.‎ ‎18.(三角函数) 函数的最小正周期为是 ‎ ‎19.(平面向量) 已知，若＝5，⊥，则向量______‎ ‎20.(三角函数) 函数的单调递减区间是__________________‎ 三、解答题（本大题共5小题，每题10分，共50分.请将详细解答过程写在答题卡上）‎ ‎21.(平面向量) 已知，，.（1）求（2）求.‎ ‎22.(三角函数)已知函数的图形的一个最高点为 ‎，由这个最高点到相邻的最低点时曲线经过，求这个函数的解析式. ‎ ‎23.(统计) 某学校900名学生在一次百米测试中，成绩全部介于秒与秒之间，抽取其中50个样本，将测试结果按如下方式分成五组：第一组，第二组，…，第五组，下图是按上述分组方法得到的频率分布直方图．‎ ‎（1）若成绩小于14秒认为优秀，求该样本在这次百米测试中成绩优秀的人数；‎ ‎（2）请估计学校900名学生中，成绩属于第四组的人数；‎ ‎（3）请根据频率分布直方图，求样本数据的众数和中位数.‎ ‎24.(概率) 某次游园的一项活动中，设置了两个中奖方案：‎ 方案1：在如图所示的游戏盘内转动一个小球，如果小球静止时停在正方形区域内则中奖；‎ 方案2：从一个装有2个红球和3个白球的袋中无放回地取出2个球，当两个球同色时则中奖.‎ 两个方案中，哪个方案中奖率更高？请说明理由.‎ ‎25.(三角变换)已知是半径为1，圆心角为的扇形，是扇形弧上的动点. 是扇形的内接矩形，记.‎ ‎（1）求当角取何值时，矩形的面积最大？并求出这个最大值.‎ ‎（2）当矩形的面积为时，求角的值.‎ 附加题：‎ ‎26. 在一次商贸交易会上，一商家在柜台开展促销抽奖活动，甲、乙两人相约同一天上午去该柜台参与抽奖. ‎ ‎（1）若抽奖规则是从一个装有6个红球和4个白球的袋中有放回地取出2个球，当两个球同色时则中奖，求中奖概率；‎ ‎（2）若甲计划在9：00～9：40之间赶到，乙计划在9：20～10：00之间赶到，求甲比乙提前到达的概率.‎ ‎27．如图，已知在三角形中，,，.‎ ‎(1) 求向量的模；‎ ‎(2)若长为的线段以点为中点，问的夹角取何值时的值最大？并求这个最大值.‎ ‎28. 在三角形中 ‎（1）若，求的值.‎ ‎（2）若，求证：.‎ 珠海市2012～2013学年度第二学期期末学生学业质量监测 高一数学试题及参考答案 一、选择题 ‎1、C　2、D　3、D　4、B　5、B　6、B　7、B　8、D　9、B　10、B　11、C　12、C 二、填空题（本大题共8小题，每小题5分，共40分,请将正确答案填在答题卡上）‎ ‎13.　　14. 　　15.　16. ‎ ‎17.　　　　18.　　　19. 　　20.‎ 三、解答题（本大题共5小题，每题10分，共50分.请将详细解答过程写在答题卡上）‎ ‎21.解：（1）‎ ‎………………………………………………………………（1分）‎ 即…………………………………………………………（3分）‎ 即………………………………………………………（4分）‎ ‎……………………………………………………………（5分）‎ ‎（2） …………………………………………………（7分）‎ 而………………（9分）‎ ‎ …………………………………………（10分）‎ ‎22、解：由题意可知：，………………………………………………………（1分）‎ ‎，即………………………………………………………（3分）‎ 由周期公式可得到：，又，…………………………（4分）‎ ‎……………………………………………………………（5分）‎ 又函数图像过点 ‎，即…………………………………（7分）‎ 又 ‎…………………………………………………………………（9分）‎ 所以函数解析式是：……………………………………（10分）‎ ‎23.解：（1）样本在这次百米测试中成绩优秀的人数=（人）……………（2分）‎ ‎（2）学校900名学生中，成绩属于第四组的人数（人）………………………（2分）‎ ‎（3）由图可知众数落在第三组，是………………………（5分）‎ 因为数据落在第一、二组的频率 数据落在第一、二、三组的频率…………（6分）‎ 所以中位数一定落在第三组中. ………………………………（7分）‎ 假设中位数是，所以……………………（9分）‎ 解得中位数…………………………………（10分）‎ ‎24.解：（1）设正方形边长为2，则圆半径为，中奖概率为.…………………（4分）‎ ‎（2）从袋中5个球中摸出2个，试验的结果共有（种）………………（5分）‎ 中奖的情况分为两种：‎ ‎（i）2个球都是红色，包含的基本事件数为；………………………………（6分）‎ ‎（ii）2个球都是白色，包含的基本事件数为.……………………………（7分）‎ 所以，中奖这个事件包含的基本事件数为1+3=4. 因此，中奖概率为.…………（9分）‎ 由于，所以方案1的中奖率更高. …………………………………………（10分）‎ ‎25.解：(1)在中：，……………………（1分）‎ 在中：‎ 所以…………………………………（2分）‎ 所以……………………………………（3分）‎ 所以矩形的面积……………………（4分）‎ ‎………………………………（6分）‎ 由，得，‎ 所以当，即时，……………（7分）‎ ‎(2) 当时，即……………（8分）‎ 又因为，所以，即…………………（10分）‎ 附加题：‎ ‎26. 在一次商贸交易会上，一商家在柜台开展促销抽奖活动，甲、乙两人相约同一天上午去该柜台参与抽奖. ‎ ‎（1）若抽奖规则是从一个装有6个红球和4个白球的袋中有放回地取出2个球，当两个球同色时则中奖，求中奖概率；‎ ‎（2）若甲计划在9：00～9：40之间赶到，乙计划在9：20～10：00之间赶到，求甲比乙提前到达的概率.‎ 解：（1）从袋中10个球中摸出2个，试验的结果共有 ‎（种）……………………………（1分）‎ 中奖的情况分为两种：‎ ‎（i）2个球都是红色，包含的基本事件数为；…………………………（2分）‎ ‎（ii）2个球都是白色，包含的基本事件数为.…………………………（3分）所以，中奖这个事件包含的基本事件数为36+16=52. 因此,中奖概率为.………………………（4分）（2）设两人到达的时间分别为9点到10点之间的x分钟、y分钟. ‎ 用表示每次试验的结果，则所有可能结果为 ‎ ；……………………………………………………………（5分）‎ 记甲比乙提前到达为事件A，则事件A的可能结果为 ‎ . ………………………………………………………（6分）‎ 如图所示，试验全部结果构成区域Ω为正方形ABCD. 而事件A所构成区域是正方形内的阴影部分. ………………………………………………………（8分）‎ 根据几何概型公式，得到 ‎ .‎ 所以，甲比乙提前到达的概率为. ………………………………（10分）‎ ‎27．如图，已知在三角形中，,，.‎ ‎(1) 求向量的模；‎ ‎(2)若长为的线段以点为中点，问的夹角取何值时的值最大？并求这个最大值.‎ 解：（1）………………………………（1分）‎ ‎……………………（2分）‎ ‎……………………（3分）‎ ‎…………………………………………………………………………………（4分）‎ ‎（另解：用几何法，根据向量加法的平行四边形法则，画图，很快可得）‎ ‎（2）……………………………………………（5分）‎ ‎……………………………………（6分）‎ ‎…………………………………………………（7分）‎ ‎……………………………………………………（8分）‎ ‎………………………………………………………（9分）‎ 当即时，……………………………（10分）‎ ‎28. 在三角形中 ‎（1）若，求的值.‎ ‎（2）若，求证：.‎ 解：（1）由得即……………………………（1分）‎ 即 即…………………………………………………（2分）‎ 即…………………………………………（3分）‎ 即 即…………………………………………………（4分）‎ ‎（2）由已知得：都为锐角，…………………………………………（5分）‎ ‎……………………………（6分）‎ ‎……………………………………………（7分）‎ 是方程的两个实根……………（8分）‎ 即 即 即或（舍去）………………………………………（9分）‎ 又因为为锐角，所以 所以…………………………………………（10分）‎