2014年普通高等学校招生全国统一考试（北京卷） 理科数学 11页

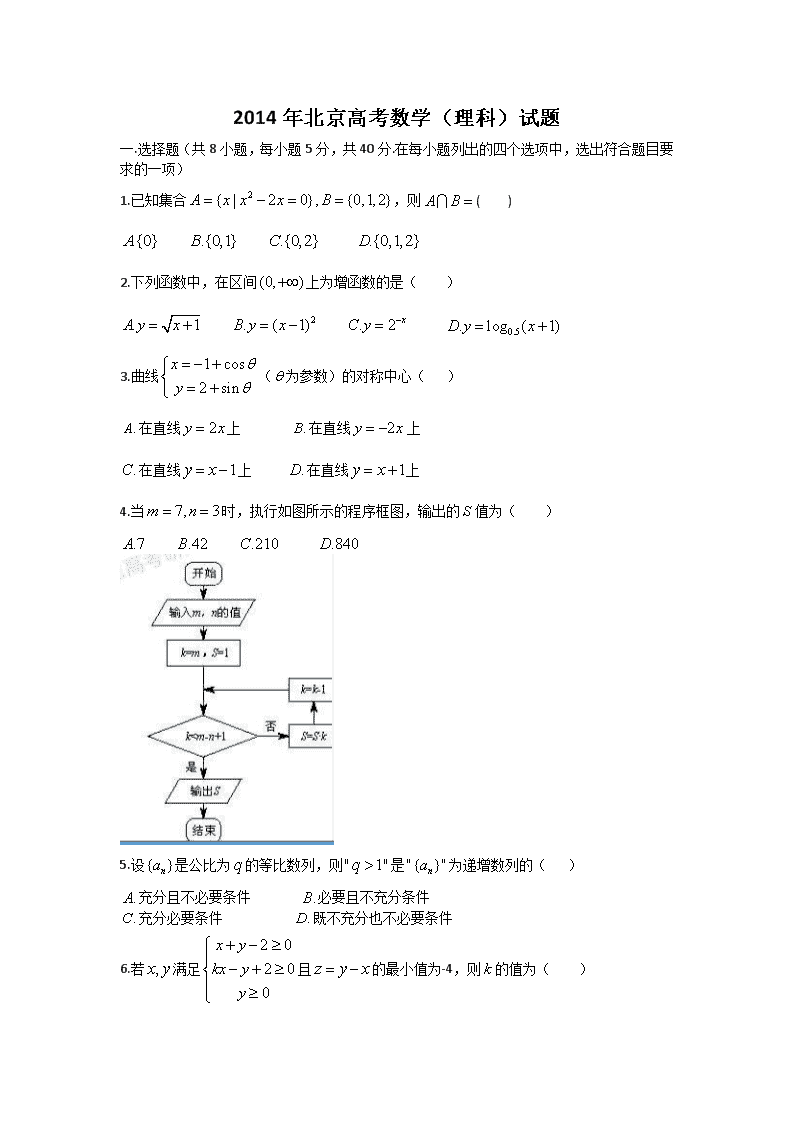
‎2014年北京高考数学（理科）试题 一.选择题（共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项）‎ ‎1.已知集合，则( )‎ ‎ ‎ ‎2.下列函数中，在区间上为增函数的是（ ）‎ ‎ ‎ ‎3.曲线（为参数）的对称中心（ ）‎ 在直线上 在直线上 ‎ 在直线上 在直线上 ‎4.当时，执行如图所示的程序框图，输出的值为（ ）‎ ‎ ‎ ‎5.设是公比为的等比数列，则是为递增数列的（ ）‎ 充分且不必要条件 必要且不充分条件 ‎ 充分必要条件 既不充分也不必要条件 ‎6.若满足且的最小值为-4，则的值为（ ）‎ ‎ ‎ 7. 在空间直角坐标系中，已知，，，，若 ‎ ，，分别表示三棱锥在，，坐标平面上的正投影图形的 ‎ 面积，则（ ）‎ ‎（A） （B）且 ‎ ‎（C）且 （D）且 ‎ 8. 有语文、数学两学科，成绩评定为“优秀”“合格”“不合格”三种.若同学每科成绩不 ‎ 低于同学，且至少有一科成绩比高，则称“同学比同学成绩好.”现有若干同学，‎ ‎ 他们之间没有一个人比另一个成绩好，且没有任意两个人语文成绩一样，数学成绩也一样 ‎ 的.问满足条件的最多有多少学生（ ）‎ ‎ （A） （B） （C） （D）‎ 二、 填空题（共6小题，每小题5分，共30分）‎ 9. 复数________.‎ 10. 已知向量、满足，，且，则________.‎ 11. 设双曲线经过点，且与具有相同渐近线，则的方程为________；‎ ‎ 渐近线方程为________.‎ 12. 若等差数列满足，，则当________时的前 ‎ 项和最大.‎ ‎13. 把5件不同产品摆成一排，若产品与产品不相邻，则不同的摆法有_______种.‎ ‎14. 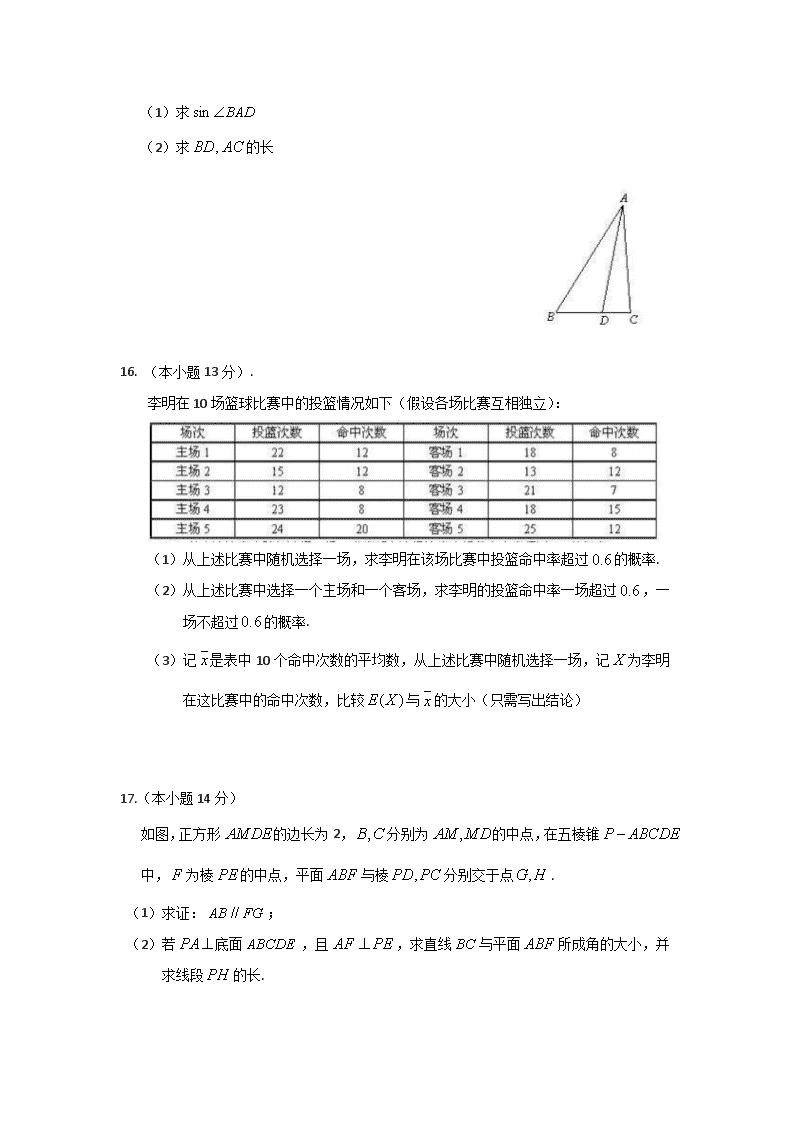设函数，，若在区间上具有单调性，且 ‎ ，则的最小正周期为________.‎ 三．解答题（共6题，满分80分）‎ ‎15. （本小题13分）如图，在中，，点在边上，且 ‎ （1）求 ‎ （2）求的长 ‎16. （本小题13分）.‎ 李明在10场篮球比赛中的投篮情况如下（假设各场比赛互相独立）：‎ ‎（1）从上述比赛中随机选择一场，求李明在该场比赛中投篮命中率超过的概率.‎ ‎（2）从上述比赛中选择一个主场和一个客场，求李明的投篮命中率一场超过，一 ‎ 场不超过的概率.‎ （3） 记是表中10个命中次数的平均数，从上述比赛中随机选择一场，记为李明 ‎ 在这比赛中的命中次数，比较与的大小（只需写出结论）‎ ‎17.（本小题14分）‎ ‎ 如图，正方形的边长为2，分别为的中点，在五棱锥 ‎ 中，为棱的中点，平面与棱分别交于点.‎ ‎ （1）求证：；‎ ‎ （2）若底面，且，求直线与平面所成角的大小，并 ‎ 求线段的长.‎ 18. ‎（本小题13分）‎ 已知函数，‎ （1） 求证：；‎ （2） 若在上恒成立，求的最大值与的最小值.‎ 19. ‎（本小题14分）‎ 已知椭圆，‎ （1） 求椭圆的离心率.‎ （2） 设为原点，若点在椭圆上，点在直线上，且，求直线与圆的位置关系，并证明你的结论.‎ ‎20.（本小题13分）‎ 对于数对序列，记，‎ ‎，其中 表示和两个数中最大的数，‎ （1） 对于数对序列，求的值.‎ （2） 记为四个数中最小值，对于由两个数对组成的数对序列和，试分别对和的两种情况比较和的大小.‎ ‎（3）在由5个数对组成的所有数对序列中，写出一个数对序列使最小，并写出的值.（只需写出结论）.‎ ‎2014年普通高等学校招生全国统一考试 数学（理）（北京卷）参考答案 一、选择题（共8小题，每小题5分，共40分）‎ ‎（1）C （2）A （3）B （4）C ‎（5）D （6）D （7）D （8）B 二、填空题（共6小题，每小题5分，共30分）‎ ‎（9）1 （10）‎ ‎（11） （12）8‎ ‎（13）36 （14）‎ 三、解答题（共6小题，共80分）‎ ‎（15）（共13分）‎ 解：（I）在中，因为，所以。‎ 所以 ‎（Ⅱ）在中，由正弦定理得 ‎，‎ 在中，由余弦定理得 所以 所以在随机选择的一场比赛中，李明的投篮命中率超过0.6的概率是05.‎ ‎（Ⅱ）设事件A为“在随机选择的一场主场比赛中李明的投篮命中率超过0.6”，‎ 事件B为“在随机选择的一场客场比赛中李明的投篮命中率超过0.6”，‎ 事件C为“在随机选择的一个主场和一个客场中，李明的投篮命中率一场超过0.6，一场不超过0.6”。‎ 则C=，A,B独立。‎ 根据投篮统计数据，.‎ ‎ ‎ ‎ ‎ ‎ ‎ 所以，在随机选择的一个主场和一个客场中，李明的投篮命中率一场超过0.6，一场不超过0.6的概率为.‎ ‎（Ⅲ）.‎ ‎（17）（共14分）‎ 解：（I）在正方形中，因为B是AM的中点，所以∥。‎ 又因为平面PDE，‎ 所以∥平面PDE，‎ 因为平面ABF，且平面平面，‎ 所以∥。‎ ‎（Ⅱ）因为底面ABCDE,所以，.‎ 如图建立空间直角坐标系，则，,,,, ‎ ‎ .‎ 设平面ABF的法向量为，则 即 令，则。所以，设直线BC与平面ABF所成角为a,则 ‎。‎ 设点H的坐标为。‎ 因为点H在棱PC上，所以可设，‎ 即。所以。‎ 因为是平面ABF的法向量，所以，即。‎ 解得，所以点H的坐标为。‎ 所以 ‎（18）（共13分）‎ 解：（I）由得 ‎ 。‎ ‎ 因为在区间上，所以在区间上单调递减。‎ 从而。‎ ‎（Ⅱ）当时，“”等价于“”“”等价于“”。‎ ‎ 令，则，‎ ‎ 当时，对任意恒成立。‎ ‎ 当时，因为对任意，，所以在区间上单调递减。从而对任意恒成立。‎ ‎ 当时，存在唯一的使得。‎ ‎ 与在区间上的情况如下：‎ ‎ ‎ ‎→‎ ‎0‎ ‎→‎ ‎↗‎ ‎↘‎ 因为在区间上是增函数，所以。进一步，“对 任意恒成立”当且仅当，即，‎ ‎ 综上所述，当且仅当时，对任意恒成立；当且仅当时，‎ 对任意恒成立。‎ ‎ 所以，若对任意恒成立，则a最大值为，b的最小值为1.‎ ‎（19）‎ 解：（I）由题意，椭圆C的标准方程为。‎ ‎ 所以，从而。因此。‎ 故椭圆C的离心率。‎ ‎（Ⅱ） 直线AB与圆相切。证明如下：‎ 设点A,B的坐标分别为，，其中。‎ 因为，所以，即，解得。‎ ‎ 当时，，代入椭圆C的方程，得，‎ ‎ 故直线AB的方程为。圆心O到直线AB的距离。‎ ‎ 此时直线AB与圆相切。‎ ‎ 当时，直线AB的方程为，‎ ‎ 即，‎ ‎ 圆心0到直线AB的距离 ‎ ‎ ‎ 又，故 ‎ ‎ ‎ 此时直线AB与圆相切。‎ ‎（20）‎ 解：（I）‎ ‎ =8‎ ‎（Ⅱ）‎ ‎ .‎ ‎ 当m=a时，==‎ ‎ 因为，且，所以≤‎ ‎ 当m=d时，‎ ‎ 因为≤，且所以≤。‎ ‎ 所以无论m=a还是m=d，≤都成立。‎ ‎（Ⅲ）数对序列（4,6），（11,11），（16,11），（11,8），（5,2）的值最小，‎ ‎ =10， =26， =42， =50， =52‎