华师大版七年级数学上复习检测：期末测试题（一） 5页

期末测试题（一）‎ 一、选择题（每小题3分，共30分）‎ ‎1．图1中的物体是一些常见的几何体，则图中可能不存在的几何体为（ ）‎ A．圆柱 B．圆锥 C．四棱柱 D．三棱柱 2． ‎－2018的绝对值是（ ）‎ A．2018 B．－2018 C． D．－‎ ‎3．为了防止某种病毒入侵电脑，可开启自动漫游，文档自动备份云端．某时刻，云文档正守护着168 888万份文档免受入侵，则数据168 888万用科学记数法可表示为（ ）‎ A．1.688 88×108 B．1.688 88×109 ‎ C．1.688 88×1010 D．16.888 8×1010‎ ‎4．如图2，∠ABC与∠DEF的大小关系为 （ ）‎ A．∠ABC>∠DEF B．∠ABC<∠DEF C．∠ABC=∠DEF D．无法确定 ‎5．有理数a，b在数轴上的对应点的位置如图3所示，则正确的结论是（　　）‎ A． b>－3 B．b<－4 C．b<－a D．b>－a ‎6．下列说法不正确的是（ ）‎ A．0是整式 B．a是代数式 C．单项式－的系数是－ D．－2x2y－1是三次二项式 7． 如图4，在直角三角形ABC中，∠B=90°，∠ACB=30°，AB=2，延长BC到D，CE平分∠ACD，则下列说法不正确的是（ ） ‎ A．点A到直线BC的距离为AB B．AB+BC>AC C．∠BCE=105° D．∠A与∠B是同旁内角 7． 如图5是一个圆柱体和一个长方体组成的几何体，圆柱的下底面紧贴在长方体的上底面上，那么这个几何体的主视图为（ ）‎ ‎9．图6是生活中一件四边形的装饰品，已知AB∥CD，∠A=∠C，则判断AD∥BC的根据是（ ）‎ A．同位角相等，两直线平行 B．内错角相等，两直线平行 C．同旁内角互补，两直线平行 D．两直线平行，同旁内角互补 ‎10．如图7所示，第1个图形中共有5个三角形，第2个图形中共有13个三角形，第3个图形中共有21个三角形，……，按照这种方法排列，则第n个图形中共有三角形 （ ）‎ A．（8n+3）个 B．（8n－3）个 C．（8n+5）个 D．（8n－5）个 二、填空题（每小题4分，共24分）‎ ‎11．近似数2.56×105精确到___________．‎ ‎12．若∠=13.8°，∠=150′，则∠－∠=________°．‎ ‎13．若单项式－2x2y2b与5y6xa+4的差是单项式，则ab=_________．‎ ‎14．将一副三角尺按图8所示放置，已知∠CBE=135°，则∠ABD的余角共有______个．‎ ‎15．图9和图10中所有的正方形大小相同，将图9的正方形放在图10中的①②③④某一位置，所组成的图形不能围成正方体的位置是_________．‎ ‎ ‎ ‎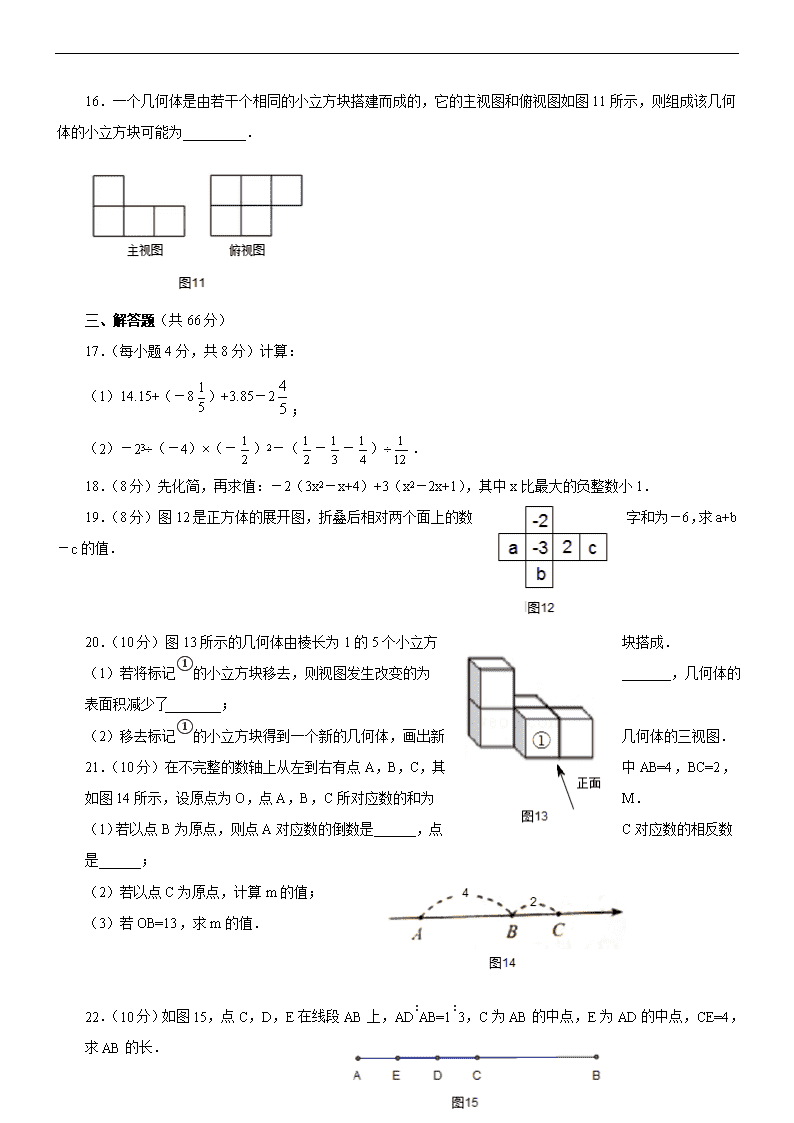16．一个几何体是由若干个相同的小立方块搭建而成的，它的主视图和俯视图如图11所示，则组成该几何体的小立方块可能为_________．‎ 三、解答题（共66分）‎ ‎17．（每小题4分，共8分）计算：‎ ‎（1）14.15+（－8）+3.85－2；‎ （2） ‎－23÷（－4）×（－）2－（－－）÷．‎ ‎18．（8分）先化简，再求值：－2（3x2－x+4）+3（x2－2x+1），其中x比最大的负整数小1．‎ ‎19．（8分）图12是正方体的展开图，折叠后相对两个面上的数字和为－6，求a+b－c的值．‎ ‎20．（10分）图13所示的几何体由棱长为1的5个小立方块搭成．‎ （1） 若将标记①的小立方块移去，则视图发生改变的为_______，几何体的表面积减少了________；‎ （2） 移去标记①的小立方块得到一个新的几何体，画出新几何体的三视图．‎ ‎21．（10分）在不完整的数轴上从左到右有点A，B，C，其中AB=4，BC=2，如图14所示，设原点为O，点A，B，C所对应数的和为M．‎ （1） 若以点B为原点，则点A对应数的倒数是______，点C对应数的相反数是______；‎ （2） 若以点C为原点，计算m的值；‎ （3） 若OB=13，求m的值．‎ ‎22．（10分）如图15，点C，D，E在线段AB上，AD∶AB=1∶3，C为AB的中点，E为AD的中点，CE=4，求AB的长．‎ 23. ‎（12分）如图16，在四边形ABCD中，已知AD∥BC，EF⊥AB，∠ABC=90°，点P是线段EF上一个动点，连接AP，BP．‎ （1） ‎∠DAP，∠CBP，∠APB之间有怎样的数量关系？并简单说明理由．‎ （2） 当点P与点E重合时，（1）的结论还成立吗？‎ （3） 当点P移动到FE的延长线上，如图17所示，那么（1）的结论还成立吗？如果不成立，写出∠DAP，∠CBP，∠APB之间的数量关系，并简单说明理由．‎ ‎（拟题 金杨建）‎ 期末测试题（一）‎ 一、1．D 2．A 3．B 4．B 5．C 6．C 7．A 8．D 9．C 10．B 二、11．千位 12．11．3 13．－8 14．4 15．① 16．6个或7个 三、17．解：（1）原式=（14.15+3.85）－（8+2）=18－11=7．‎ ‎（2）原式=－8÷（－4）×－（－－）×12=2×－（×12－×12－×12）=－（6－4－3）=－（－1）=+1=．‎ ‎18．解：原式=－6x2+2x－8+3x2－6x+3=－3x2－4x－5．‎ 因为最大的负整数为－1，所以x=－1－1=－2．‎ 当x=－2时，原式=－3×（－2）2－4×（－2）－5=－12+8－5=－9．‎ ‎19．解：根据题意，得a+2=－6，b－2=－6，c－3=－6．‎ 所以a=－6－2=－8，b=－6+2=－4，c=－6+3=－3．‎ 所以a+b－c=－8－4－（－3）=－8－4+3=－9．‎ ‎20．解：（1）俯视图 2‎ ‎（2）如图所示：‎ ‎21．解：（1）－ －2‎ ‎（2）由题意可知，点A，B，C所对应的数分别为－6，－2，0，所以m=－6－2+0=－8．‎ ‎（3）①若点O在点B的左边，则点A，B，C所对应的数分别为9，13，15，所以m=9+13+15=37．‎ ‎②若点O在点B的右边，则点A，B，C所对应的数分别为－17，－13，－11，所以m=‎ ‎－17－13－11=－41．‎ 综上可知，m的值为37或－41．‎ ‎22．解：因为AD∶AB=1∶3，所以AD=AB．‎ 因为E为AD的中点，所以AE=AD=×AB=AB．‎ 因为C为AB的中点，所以AC=AB．‎ 因为AC－AE=CE=4，所以AB－AB=4，即（－）AB=4，解得AB=12（cm）．‎ ‎23．解：（1）∠DAP+∠CBP=∠APB．理由如下：‎ 因为∠ABC=90°，所以BC⊥AB．‎ 因为EF⊥AB，所以EF∥BC．所以∠CBP=∠BPE．‎ 又因为AD∥BC，所以AD∥EF，所以∠DAP=∠APE．‎ 所以∠DAP+∠CBP=∠APE+∠BPE=∠APB．‎ ‎（2）成立．‎ ‎（3）（1）的结论不成立，∠DAP+∠CBP+∠APB=360°．理由如下：‎ 因为AD∥EF，所以∠DAP+∠APE=180°．‎ 因为EF∥BC，所以∠CBP+∠BPE=180°．‎ 所以∠DAP+∠CBP+∠APB=∠DAP+∠APE+∠CBP+∠BPE=180°+180°=360°．‎