- 195.50 KB
- 2021-10-21 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
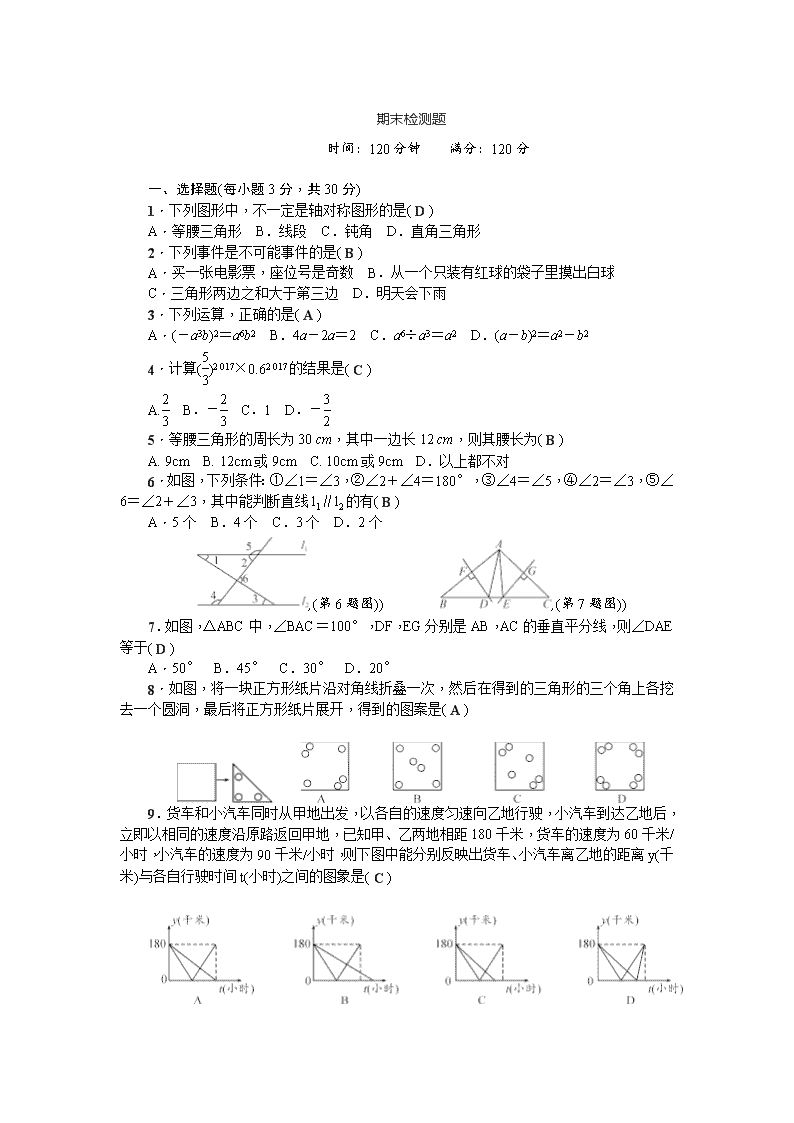
期末检测题
时间:120 分钟 满分:120 分
一、选择题(每小题 3 分,共 30 分)
1.下列图形中,不一定是轴对称图形的是( D )
A.等腰三角形 B.线段 C.钝角 D.直角三角形
2.下列事件是不可能事件的是( B )
A.买一张电影票,座位号是奇数 B.从一个只装有红球的袋子里摸出白球
C.三角形两边之和大于第三边 D.明天会下雨
3.下列运算,正确的是( A )
A.(-a3b)2=a6b2 B.4a-2a=2 C.a6÷a3=a2 D.(a-b)2=a2-b2
4.计算(5
3)2 017×0.62 017 的结果是( C )
A.2
3 B.-2
3 C.1 D.-3
2
5.等腰三角形的周长为 30 cm,其中一边长 12 cm,则其腰长为( B )
A. 9cm B. 12cm 或 9cm C. 10cm 或 9cm D.以上都不对
6.如图,下列条件:①∠1=∠3,②∠2+∠4=180°,③∠4=∠5,④∠2=∠3,⑤
∠6=∠2+∠3,其中能判断直线 l1∥l2 的有( B )2
A.5 个 B.4 个 C.3 个 D.2 个
,(第 6 题图)) ,(第 7 题图))
7.如图,△ABC 中,∠BAC=100°,DF,EG 分别是 AB,AC 的垂直平分线,则∠DAE
等于( D )
A.50° B.45° C.30° D.20°
8.如图,将一块正方形纸片沿对角线折叠一次,然后在得到的三角形的三个角上各挖
去一个圆洞,最后将正方形纸片展开,得到的图案是( A )
9.货车和小汽车同时从甲地出发,以各自的速度匀速向乙地行驶,小汽车到达乙地后,
立即以相同的速度沿原路返回甲地,已知甲、乙两地相距 180 千米,货车的速度为 60 千米/
小时,小汽车的速度为 90 千米/小时,则下图中能分别反映出货车、小汽车离乙地的距离 y(千
米)与各自行驶时间 t(小时)之间的图象是( C )
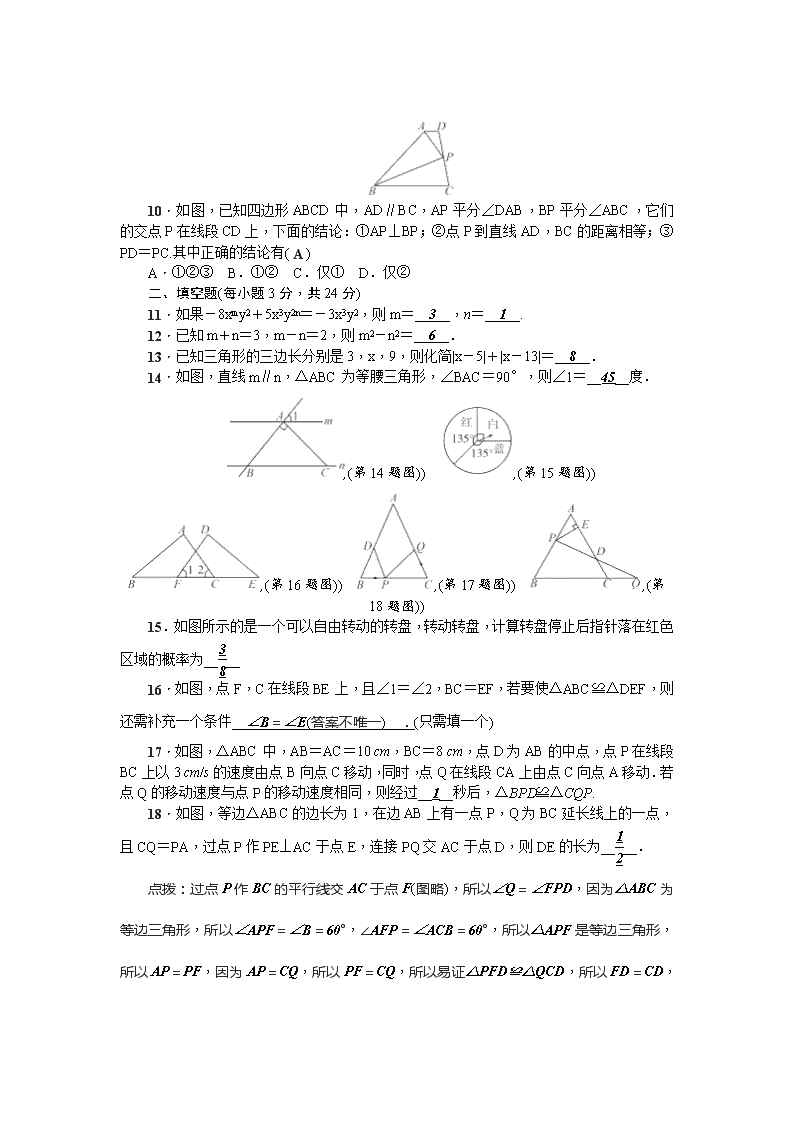
10.如图,已知四边形 ABCD 中,AD∥BC,AP 平分∠DAB,BP 平分∠ABC,它们
的交点 P 在线段 CD 上,下面的结论:①AP⊥BP;②点 P 到直线 AD,BC 的距离相等;③
PD=PC.其中正确的结论有( A )
A.①②③ B.①② C.仅① D.仅②
二、填空题(每小题 3 分,共 24 分)
11.如果-8xmy2+5x3y2n=-3x3y2,则 m=__3__,n=__1__.
12.已知 m+n=3,m-n=2,则 m2-n2=__6__.
13.已知三角形的三边长分别是 3,x,9,则化简|x-5|+|x-13|=__8__.
14.如图,直线 m∥n,△ABC 为等腰三角形,∠BAC=90°,则∠1=__45__度.
,(第 14 题图)) ,(第 15 题图))
,(第 16 题图)) ,(第 17 题图)) ,(第 18
题图))
15.如图所示的是一个可以自由转动的转盘,转动转盘,计算转盘停止后指针落在红色
区域的概率为__3
8__
16.如图,点 F,C 在线段 BE 上,且∠1=∠2,BC=EF,若要使△ABC≌△DEF,则
还需补充一个条件__∠B=∠E(答案不唯一)__.(只需填一个)
17.如图,△ABC 中,AB=AC=10 cm,BC=8 cm,点 D 为 AB 的中点,点 P 在线段
BC 上以 3 cm/s 的速度由点 B 向点 C 移动,同时,点 Q 在线段 CA 上由点 C 向点 A 移动.若
点 Q 的移动速度与点 P 的移动速度相同,则经过__1__秒后,△BPD≌△CQP.
18.如图,等边△ABC 的边长为 1,在边 AB 上有一点 P,Q 为 BC 延长线上的一点,
且 CQ=PA,过点 P 作 PE⊥AC 于点 E,连接 PQ 交 AC 于点 D,则 DE 的长为__1
2__.
点拨:过点 P 作 BC 的平行线交 AC 于点 F(图略),所以∠Q=∠FPD,因为△ABC 为
等边三角形,所以∠APF=∠B=60°,∠AFP=∠ACB=60°,所以△APF 是等边三角形,
所以 AP=PF,因为 AP=CQ,所以 PF=CQ,所以易证△PFD≌△QCD,所以 FD=CD,
因为 PE⊥AC,△APF 是等边三角形,所以 AE=EF,所以 AE+DC=EF+FD,所以 ED
=1
2AC=1
2.
三、解答题(共 66 分)
19.(9 分)用简便方法计算.
(1)594
5
×601
5
; (2)992;
解:(1)原式=(60-1
5)×(60+1
5)=602-(1
5)2=3 59924
25
(2)原式=(100-1)2=9 801
(3)(x
2
+5)2-(x
2
-5)2.
解:原式=(x
2+5+x
2-5)×(x
2+5-x
2+5)=10x
20.(10 分)(1)化简:(3m2n)3·(-2mn2)2·n-(2m2)4·(-3n4)2;
解:原式=27m6n3·4m2n4·n-16m8·9n8=108m8n8-144m8n8=-36m8n8.
(2)先化简,再求值:(a2b-ab2)÷b+(3-a)(3+a),其中 a=1
4
,b=8.
解:原式=a2-ab+9-a2=-ab+9,当 a=1
4
,b=8 时,原式=-1
4
×8+9=7.
21.(7 分)如图,有公路 l1 同侧、l2 异侧的两个城镇 A,B,电信部门要修建一座信号发
射塔,按照设计要求,发射塔到两个城镇 A,B 的距离必须相等,到两条公路 l1,l2 的距离
也必须相等,发射塔 C 应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点 C
的位置.(保留作图痕迹,不要求写出画法)
解:作图略,作 l1、l2 所夹角的平分线及线段 AB 的垂直平分线,有两个交点,即 C1,
C2 符合题意.
22.(8 分)在一个不透明的袋中装有 2 个黄球,3 个黑球和 5 个红球,它们除颜色外其
他都相同.
(1)将袋中的球摇匀后,求从袋中随机摸出一个球是黄球的概率;
(2)现在再将若干个红球放入袋中,与原来的 10 个球均匀混合在一起,使从袋中随机摸
出一个球是红球的概率是2
3
,请求出后来放入袋中的红球的个数
解:(1)因为共 10 个球,有 2 个黄球,所以 P(黄球)= 2
10=1
5.
(2)设后来有 x 个红球放入袋中,根据题意,得(10+x)×2
3=5+x,解得 x=5,故后来
放入袋中的红球有 5 个
23.(10 分)如图,在四边形中 ABCD 中,AB∥CD,∠1=∠2,DB=DC.
(1)试说明:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE 的度数.
解:(1)因为 AB∥CD,所以∠ABD=∠EDC,在△ABD 和△EDC 中,
∠1=∠2,
DB=DC,
∠ABD=∠EDC,
所以△ABD≌△EDC(ASA)
(2)因为∠ABD=∠EDC=30°,∠A=135°,所以∠1=∠2=15°,因为 DB=DC,
所以∠DCB=180°-∠BDC
2
=75°,所以∠BCE=75°-15°=60°.
24.(10 分) 小红与小兰从学校出发到距学校 5 千米的书店买书,如图反应了他们两人
离开学校的路程与时间的关系.请根据图形解决问题.2-1-c-n-j-y
(1)小红与小兰谁先出发?早出发几分钟?
(2)小兰前 20 分钟的速度和最后 10 分钟的速度各是多少?
(3)小红与小兰从学校到书店的平均速度各是多少?
解:(1)小兰比小红先出发,早出发了 10 分钟.
(2)小兰前 20 分钟的速度为 2÷1
3=6(千米/小时),最后 10 分钟的速度为(5-2)÷1
6=18(千
米/小时).2·1·c·n·j·y
(3)小兰的平均速度为 5÷1=5(千米/小时),小红的平均速度为 5÷5
6=6(千米/小时).
25.(12 分) 已知△ABC,点 D,F 分别为线段 AC,AB 上两点,连接 BD,CF 交于点
E.
(1)若 BD⊥AC,CF⊥AB,如图 1 所示,试说明:∠BAC+∠BEC=180°;
(2)若 BD 平分∠ABC,CF 平分∠ACB,如图 2 所示,试说明此时∠BAC 与∠BEC 的
数量关系;
(3)在(2)的条件下,若∠BAC=60°,试说明:EF=ED.
解:(1)因为 BD⊥AC,CF⊥AB,所以∠DCE+∠DEC=∠DCE+∠FAC=90°,所以
∠DEC=∠BAC,因为∠DEC+∠BEC=180°,所以∠BAC+∠BEC=180°.(2)因为 BD
平分∠ABC,CF 平分∠ACB,所以∠EBC=1
2
∠ABC,∠ECB=1
2
∠ACB,所以∠BEC=180°
-(∠EBC+∠ECB)=180°-1
2(∠ABC+∠ACB)=180°-1
2(180°-∠BAC)=90°+
1
2
∠BAC.(3)作∠BEC 的平分线 EM 交 BC 于点 M,因为∠BAC=60°,所以∠BEC=90°
+1
2
∠BAC=120°,所以∠FEB=∠DEC=60°,因为 EM 平分∠BEC,所以∠BEM=60°,
在△EBF 与△EBM 中,
∠FBE=∠EBM,
BE=BE,
∠FEB=∠MEB,
所以△EBF≌△EBM,所以 EF=EM,同理
DE=EM,所以 EF=DE.
相关文档
- 河南七年级道德与法治上册期末检测2021-10-2133页
- 北师版七年级数学上册-期末检测题2021-10-215页
- 2020七年级数学上册 期末检测题 (新2021-10-216页
- 新人教版七年级数学上册期末检测题2021-10-214页
- 银川市2010—2011学年第一学期期末2021-10-126页
- 黑龙江省大庆市林甸县2014—2015学2021-10-1210页
- 银川市2010—2011学年第一学期期末2021-10-126页
- 九年级英语上册期末检测卷课件 外2021-10-1236页
- 外研初中二年级英语期末检测题A2021-10-127页
- 海南省海口市2012-2013学年八年级2021-10-129页