青岛初中数学七年级下册10.3三元一次方 程组 20页

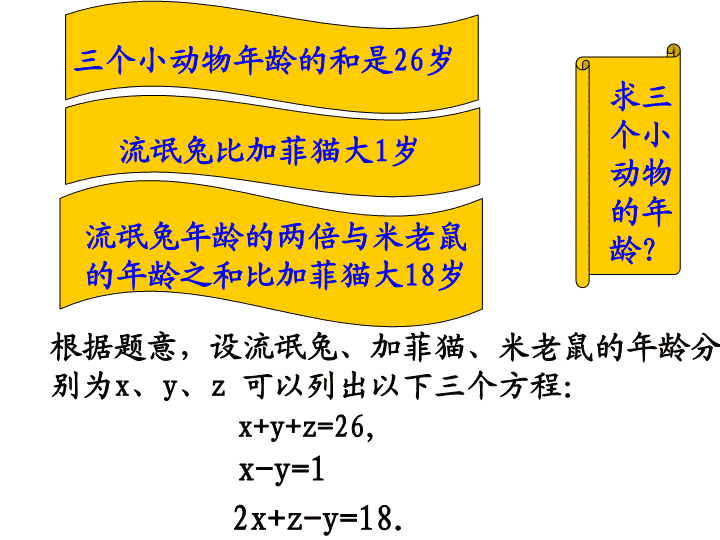
10.3三元一次方程组 流氓兔比加菲猫大1岁流氓兔年龄的两倍与米老鼠的年龄之和比加菲猫大18岁求三个小动物的年龄?三个小动物年龄的和是26岁x+y+z=26,x-y=12x+z-y=18．根据题意，设流氓兔、加菲猫、米老鼠的年龄分别为x、y、z可以列出以下三个方程： （一）三元一次方程含有三个未知数，并且含有未知数的项的次数都是1，像这样的整式方程叫做三元一次方程。定义 （二）三元一次方程组解:设流氓兔x岁，加菲猫y岁，米老鼠z岁，x＋y+z=26，①x-y=1，②2x+z-y=18．③组合在一起这样就构成了方程组x+y+z=26①x-y=1②2x+z-y=18③ 含有三个相同的未知数，每个方程中含有未知数的项的次数都是1，像这样的方程组叫做三元一次方程组三元一次方程组如何定义?x＋y+z=26，x-y=1，2x+z-y=18.含有三个未知数未知数的项次数都是一次特点定义 辨析判断下列方程组是不是三元一次方程组?方程个数不一定是三个,但至少要有两个。方程中含有未知数的个数是三个√×①② ③×方程中含有未知数的项的次数都是一次x+y=20y+z=19x+z=21√方程组中一共有三个未知数④辨析 代入消元法2、解二元一次方程组的基本思路是什么？消元一元一次方程二元一次方程组消元1、解二元一次方程组的方法有哪些？加减消元法 三元一次方程组一元一次方程二元一次方程组1.化“三元”为“二元”总结消元消元三元一次方程组求法步骤：2.化“二元”为“一元”怎样解三元一次方程组？（也就是消去一个未知数） 例1解方程组x-z=4.③2x+2z=2①＋②，得④1.化“三元”为“二元”考虑消去哪个未知数（也就是三个未知数要去掉哪一个?）2.化“二元”为“一元”。x-y+z=0②x+y+z=2①x-z=4③④解法一：消去y ①③②解法二：消去x由③得，x=z+4④把④代入①、②得，2z+y=-2⑦2z-y=-4⑧（z+4)+y+z=2⑤(z+4)-y+z=0⑥化简得， ①③②解法三：消去z由③得，z=x-4④把④代入①、②得2x+y=6⑦4-y=0⑧x+y+(x-4)=2,⑤x-y+(x-4)=0,⑥化简得， 注：如果三个方程中有一个方程是二元一次方程（如例1中的③），则可以先通过对另外两个方程组进行消元，消元时就消去三个元中这个二元一次方程（如例1中的③）中缺少的那个元。缺某元，消某元。①③②在三元化二元时，对于具体方法的选取应该注意选择最恰当、最简便的方法。 解：　①＋②，得2x+2z=2,化简，得x+z=1④③+④,得①③②把　　　代入③，得x=2x=5x-z=4③x+z=1④∴,把代入②，得y=1所以，原方程组的解是 课堂练习x+y+z=12,x+2y+5z=22,x=4y. ①③②1.化“三元”为“二元”解：③－②，得④④①2.化“二元”为“一元”例2解方程组原方程组中有哪个方程还没有用到？ 例2解方程组①③②解:③-②，得①+④，得∴④所以,原方程组的解是把x=1代入方程①、③，分别得 ④①①③②1.化“三元”为“二元”解：　③－②，得④例2解方程组原方程组中有哪个方程还没有用到？可不可以不用①？④②④③在消去一个未知数得出比原方程组少一个未知数的二元一次方程组的过程中，原方程组的每一个方程一般都至少要用到一次．可不可以只用方程组中的两个就求解出方程的解？ 例2也可以这样解:①+②+③,得即，⑤－①,得⑤－②,得①③②⑤－③，得所以，原方程组的解是⑤④ 小结（一）三元一次方程组的概念是什么?（二）解三元一次方程组的基本思路是什么?（三）在三元化二元时，对于具体方法的选取应该注意什么？