北师版七年级数学下册-第二章检测题 6页

第二章检测题(时间：120分钟满分：120分)一、选择题(每小题3分，共30分)1．如图所示，∠1与∠2不是同旁内角的是(D)2．点P是直线l外一点，点A，B，C在直线l上，若PA＝4cm，PB＝5cm，PC＝6cm，则点P到直线l的距离是(C)A．4cmB．小于4cmC．不大于4cmD．5cm3．如图，AB∥CD，∠A＝45°，∠C＝28°，则∠AEC的大小为(D)A．17°B．62°C．63°D．73°,第4题图),第5题图)4．(济南中考)如图，AF是∠BAC的平分线，DF∥AC，若∠1＝35°，则∠BAF的度数为(B)A．17.5°B．35°C．55°D．70°5．如图，下列推理正确的是(D)A．因为∠1＝∠2，所以DE∥BFB．因为∠1＝∠2，所以CE∥AFC．因为∠CEF＋∠AFE＝180°，所以DE∥BFD．因为∠CEF＋∠AFE＝180°，所以CE∥AF6．如图，直线AB与CD相交于点O，EO⊥CD，垂足为O，则图中∠AOE和∠BOD的关系是(D)A．相等角B．互为补角C．对顶角D．互为余角,第6题图),第8题图),第9题图)7．一辆汽车在公路上行驶，两次拐弯后，仍在原来的方向上平行行驶，那么两个拐弯的角度可以是(B)A．先向左转130°，再向左转50°B．先向左转50°，再向右转50°C．先向左转50°，再向右转40°D．先向左转50°，再向左转40° 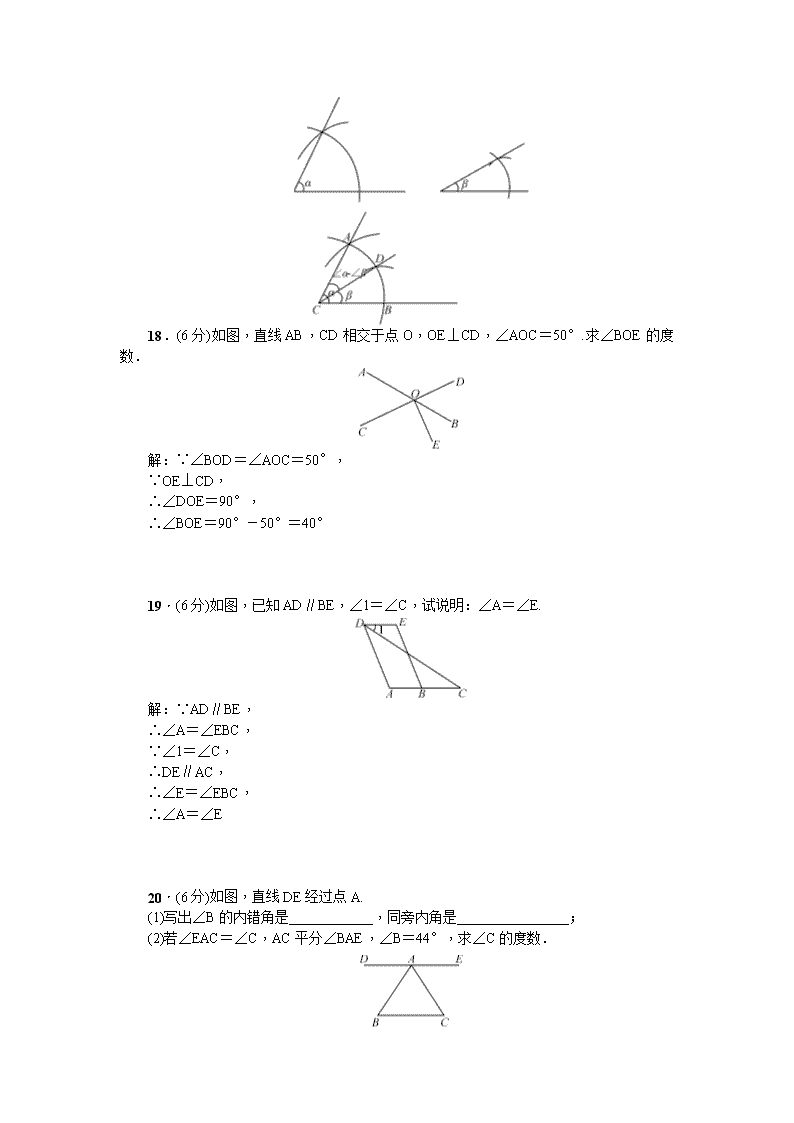8．如图，EF⊥MN，垂足为F，且∠1＝140°，则当∠2等于多少时，AB∥CD(A)A．50°B．40°C．30°D．60°9．如图，直线l1∥l2，∠CAB＝125°，∠ABD＝85°，则∠1＋∠2等于(A)A．30°B．35°C．36°D．40°10．如图，a∥b，∠1＝65°，∠2＝140°，则∠3等于(B)A．100°B．105°C．110°D．115°二、填空题(每小题3分，共18分)11．如果一个角的余角是40°，那么这个角的补角是130°.12．如图，将一张长方形纸条折叠，∠2＝60°，则∠1＝60°.,第12题图),第13题图),第14题图)13．如图，已知∠1＝∠2，则图中互相平行的线段是AD∥BC.14．因修建公路需要在某处开凿一条隧道，为了加快进度，决定在如图所示的A，B两处同时开工．如果在A地测得隧道方向为北偏东62°，那么在B地应按南偏西62°方向施工，就能保证隧道准确接通．15．如图，一个含有30°角的直角三角形的两个顶点放在一个长方形的对边上，若∠1＝25°，则∠2＝115°.,第15题图),第16题图)16．如图，AD平分∠CAE，CF∥AD，∠1＝80°，∠2＝100°.三、解答题(共72分)17．(6分)已知∠α，∠β，用直尺和圆规，求作角，使它等于∠α－∠β.(要求保留作图痕迹，在所作图中标上必要的字母，不要求写作法)解：如图，∠ACD即为所求 18．(6分)如图，直线AB，CD相交于点O，OE⊥CD，∠AOC＝50°.求∠BOE的度数．解：∵∠BOD＝∠AOC＝50°，∵OE⊥CD，∴∠DOE＝90°，∴∠BOE＝90°－50°＝40°19．(6分)如图，已知AD∥BE，∠1＝∠C，试说明：∠A＝∠E.解：∵AD∥BE，∴∠A＝∠EBC，∵∠1＝∠C，∴DE∥AC，∴∠E＝∠EBC，∴∠A＝∠E20．(6分)如图，直线DE经过点A.(1)写出∠B的内错角是____________，同旁内角是________________；(2)若∠EAC＝∠C，AC平分∠BAE，∠B＝44°，求∠C的度数． 解：(1)∠B的内错角是∠BAD，∠B的同旁内角是∠BAC，∠EAB和∠C(2)∵∠EAC＝∠C，∴DE∥BC，∴∠BAE＝180°－44°＝136°，∵AC平分∠BAE，∴∠EAC＝68°，∴∠C＝∠EAC＝68°21．(8分)如图，已知AB∥CD，∠B＝40°，CN是∠BCE的平分线CM⊥CN.(1)求∠BCE的度数；(2)求∠BCM的度数．解：(1)∵AB∥CD，∴∠BCE＋∠B＝180°.∵∠B＝40°，∴∠BCE＝180°－40°＝140°(2)∵CN是∠BCE的平分线，∴∠BCN＝∠BCE＝×140°＝70°.∵CM⊥CN，∴∠BCM＝90°－70°＝20°22．(8分)(1)如图1，O是直线AB上一点，OE平分∠AOC，OF平分∠BOC，试说明OE⊥OF；(2)如图2，AB∥CD，∠1＝∠B，∠2＝∠D.说明BE⊥DE的理由．(1)解：∵OE平分∠AOC，OF平分∠BOC，∴∠EOC＝∠AOC，∠FOC＝BOC，∵∠AOC＋∠BOC＝180°，∴∠EOF＝∠EOC＋∠FOC＝90°，∴OE⊥OF(2)解：∵AB∥CD，∴∠A＋∠C＝180°，∵∠2＋∠D＋∠C＝180°，∠1＋∠A＋∠B＝180°，∠1＝∠B，∠2＝∠D，∴2∠1＋2∠2＝180°＋180°－180°＝180°，∴∠1＋∠2＝90°，∴∠BED＝90°，∴BE⊥DE23．(10分)如图，台球运动中，如果母球P击中边点A，经桌边反弹后击中相邻的另一桌边的点B，两次反弹．(1)若∠PAD＝32度，求∠PAB的度数；(2)母球P经过的路线BC与PA一定平行吗？请说明理由． 解：(1)∵∠PAD＝32°，∠PAD＝∠BAE，∠PAD＋∠PAB＋∠BAE＝180°，∴∠PAB＝180°－32°－32°＝116°(2)BC∥PA，理由如下：∵∠PAD＝∠BAE，∠PAB＝180°－∠PAD－∠BAE，∴∠PAB＝180°－2∠BAE.同理：∠ABC＝180°－2∠ABE.∵∠BAE＋∠ABE＝90°，∴∠PAB＋∠ABC＝360°－2(∠BAE＋∠ABE)＝180°.∴BC∥PA24．(10分)已知：如图，点C在∠AOB的一边OA上，过点C的直线DE∥OB，CF平分∠ACD，CG⊥CF于点C.(1)若∠O＝38°，求∠ECF的度数；(3分)(2)试说明CG平分∠OCD的理由；(3分)(3)当∠O为多少度时，CD平分∠OCF，请说明理由．(4分)解：(1)∵DE∥OB，∠O＝38°，∴∠ACE＝∠O＝38°，∵∠ACD＋∠ACE＝180°，∴∠ACD＝142°，∵CF平分∠ACD，∴∠ACF＝∠ACD＝71°，∴∠ECF＝∠ACE＋∠ACF＝109°(2)∵CG⊥CF，∴∠FCG＝90°，∴∠DCG＋∠DCF＝90°，又∵∠GCO＋∠DCG＋∠DCF＋∠ACF＝180°，∴∠GCO＋∠FCA＝90°，∵∠ACF＝∠DCF，∴∠GCO＝∠GCD，即CG平分∠OCD(3)当∠O＝60°时，CD平分∠OCF.理由如下：当∠O＝60°时，∵DE∥OB，∴∠DCO＝∠O＝60°，∴∠ACD＝120°，又∵CF平分∠ACD，∴∠DCF＝60°，∴∠DCO＝∠DCF，即CD平分∠OCF25．(12分)观察发现：已知AB∥CD，点P是平面上一个动点．当点P在直线AB，CD的异侧，且在BC(不与点B，C重合)上时，如图①，容易发现：∠ABP＋∠DCP＝∠BPC.拓展探究： (1)当点P位于直线AB，CD的异侧，且在BC左侧时，如图②，∠ABP，∠DCP，∠BPC之间有何关系？并说明理由；(2)当点P位于直线AB，CD的异侧，且在BC右侧时，如图③，∠ABP，∠DCP，∠BPC之间有何关系？并说明理由；(3)当点P位于直线AB，CD的同侧，如图④，∠ABP，∠DCP，∠BPC之间有何关系？并说明理由．解：(1)∠ABP＋∠DCP＝∠BPC.理由：如图，过点P作直线PQ∥AB，∴∠ABP＝∠BPQ(两直线平行，内错角相等)，∵AB∥CD(已知)，∴DC∥PQ(如果两条直线和第三条直线平行，那么这两条直线平行)，∴∠DCP＝∠CPQ(两直线平行，内错角相等)，∴∠ABP＋∠DCP＝∠BPQ＋∠CPQ＝∠BPC(等量代换)(2)∠ABP＋∠BPC＋∠DCP＝360°，理由：如图③，过P作PQ∥AB，则DC∥PQ，∴∠ABP＋∠BPQ＝180°，∠DCP＋∠CPQ＝180°，∴∠ABP＋∠BPC＋∠DCP＝360°(3)∠BPC＝∠DCP－∠ABP，理由：如图④，过P作PQ∥AB，则PQ∥DC，∴∠DCP＝∠CPQ，∠ABP＝∠BPQ，∴∠BPC＝∠CPQ－∠BPQ＝∠DCP－∠ABP