幂的乘方与积的乘方教案 4页

‎ ‎ ‎8.2幂的乘方与积的乘方（1）‎ 教学目标：‎ ‎1．能说出幂的乘方与积的乘方的运算性质，并会用符号表示。‎ ‎2．会运用幂的乘方与积的乘方的运算性质进行运算，并能说出每一步运算的依据。‎ ‎3．经历探索幂的乘方与积的乘方的运算性质的过程，进一步体会幂的意义，从中感受具体到抽象、特殊到一般的思考方法，发展数感和归纳的能力。‎ 教学内容 个人主页 ‎（一）情境创设：‎ 除课本提供的情境外，教学中还可以举一些学生熟悉的问题，比如，一个正方人本的棱长是100mm，即102mm，它的体积是多少？引导学生体会进行幂的乘方运算的必要性。‎ ‎（二）探索活动 问题一 我们知道100个104相乘可以记作（104）100，你能说说（23）2、（54）3的意义吗？‎ 问题二 请你计算（23）2、（54）3，并说明每一步计算的理由。‎ 问题三 你能说说（a3）4（x4）3的意义吗？‎ 问题四 请你计算（a3）4、（x4）3，并说明每一步计算的理由。‎ 问题五 从上面的计算中你发现什么规律？能说明你的猜想是正确的吗？‎ ‎（三）例题教学 例1 计算 ‎(1)(106)2; (2)(am)4(m是正整数);‎ ‎(3)－(y3)2 (4)(－x3)3‎ 例1的教学，建议不要直接套用公式写出结果，通过写出计算过程，以引导学生逐步熟悉“幂的乘方的运算性质”；‎ 例2 计算 ‎(1)x2·x4+(x3)2； (2)(a3)3·(a4)3‎ 例2的教学，应让学生在说明算理的基础上，充分交流各自的做法，以利于正确的理解和区别幂的乘方运算性质和同底数幂的乘法运算性质。‎ ‎ 例3 ①已知(b2·bx)2=b12，求x的值。‎ ‎②求27m·qn的值。‎ ‎③比较2555,3444,4333的大小（增加性质的逆应用）‎ 4‎ ‎ ‎ ‎4、思维拓展 建议本节课进行一些幂的乘方运算性质的逆向运用的训练，逐步培养学生逆向思维的习惯。如：‎ ‎（１）填空：‎ ‎①108＝（ ）２；　　　　　　　　　 ②b27＝(b３)( )；‎ ‎③(ym）3＝（ ）m；　　　　　　　　　 ④p２n＋２＝( )2。‎ ‎（２）请你比较３４０与４３０的大小。‎ ‎（3）已知2x+5y－7=0，求4x，32y的值。‎ ‎５、小结 ‎（１）说说幂的乘方的运算性质；‎ ‎（２）举例说明幂的乘方运算性质与同底数幂的乘法运算性质的联系与区别。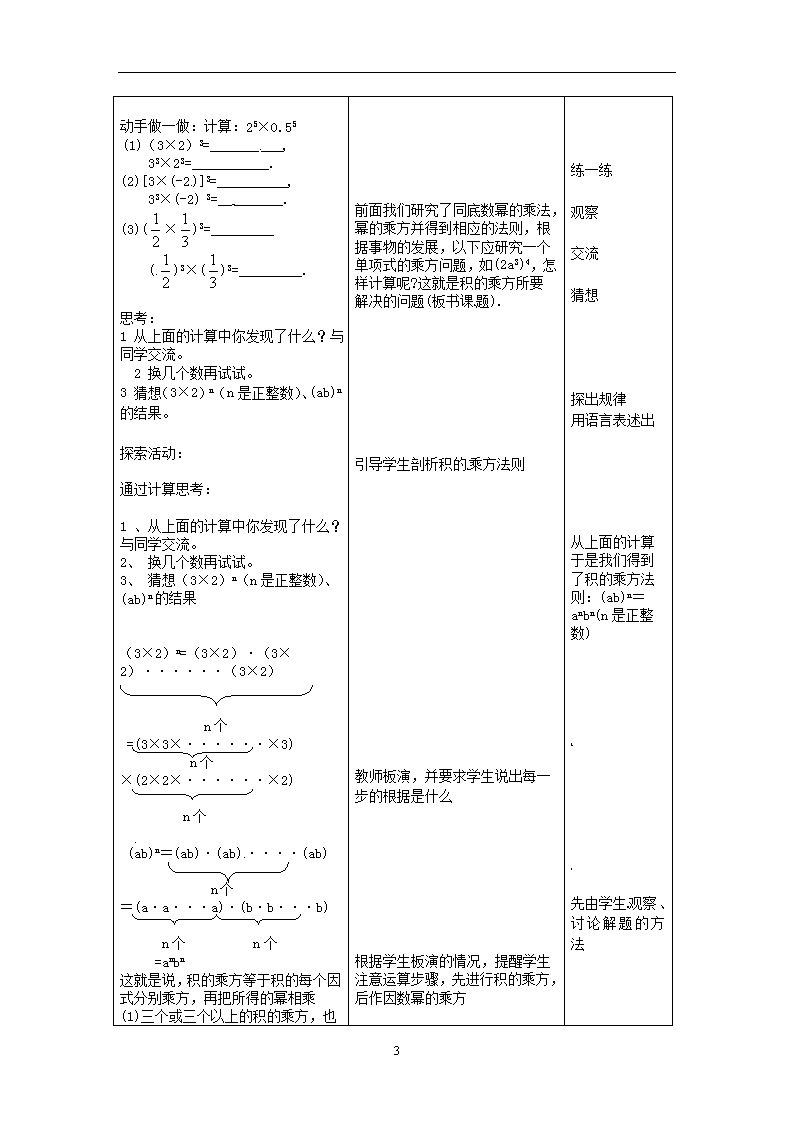‎ ‎ ‎ ‎8.2幂的乘方与积的乘方（2）‎ 课时编号 ‎3‎ 备课时间 课 题 ‎8.2幂的乘方和积的乘方（2）‎ 教学目标 ‎1、经历积的乘方运算性质的探索过程，进一步理解幂的意义； ‎2、使学生能灵活地运用积的乘方法则进行计算，并会解决一些实际问题； 3、通过法则的推导过程培养学生分析问题、解决问题的能力；‎ ‎4、从中感受具体到抽象、特殊到一般的思考方法，发展数感和归纳的能力 教学重点 法则的理解与掌握 教学难点 法则的灵活运用 教 学 过 程 教学内容 教师活动 学生活动 4‎ ‎ ‎ 动手做一做：计算：25×0.55‎ ‎(1)（3×2）3=__________,‎ ‎33×23=___________.‎ ‎(2)[3×(-2)]3=__________,‎ ‎33×(-2) 3=_________.‎ ‎(3)(×)3=_________‎ ‎()3×()3=_________.‎ 思考：‎ ‎1 从上面的计算中你发现了什么？与同学交流。‎ ‎ 2 换几个数再试试。‎ ‎3 猜想（3×2）n（n是正整数）、(ab)n的结果。‎ 探索活动：‎ 通过计算思考：‎ ‎1 、从上面的计算中你发现了什么？与同学交流。‎ ‎2、 换几个数再试试。‎ ‎3、 猜想（3×2）n（n是正整数）、(ab)n的结果 ‎（3×2）n=（3×2）·（3×2）······（3×2）‎ ‎ ‎ ‎ n个 ‎ =(3×3×······×3) ‎ n个 ‎×(2×2×······×2)‎ n个 ‎ ‎ ‎ (ab)n＝(ab)·(ab)····(ab)‎ ‎ ‎ ‎ n个 ‎＝(a·a···a)·(b·b···b)‎  ‎ n个 n个 ‎ =anbn 这就是说，积的乘方等于积的每个因式分别乘方，再把所得的幂相乘 前面我们研究了同底数幂的乘法，幂的乘方并得到相应的法则，根据事物的发展，以下应研究一个单项式的乘方问题，如(2a3)4，怎样计算呢?这就是积的乘方所要解决的问题(板书课题).‎ 引导学生剖析积的乘方法则 教师板演，并要求学生说出每一步的根据是什么 根据学生板演的情况，提醒学生注意运算步骤，先进行积的乘方，后作因数幂的乘方 练一练 观察 交流 猜想 探出规律 用语言表述出 从上面的计算于是我们得到了积的乘方法则：(ab)n＝anbn(n是正整数) 先由学生观察、讨论解题的方法 4‎ ‎ ‎ ‎(1)三个或三个以上的积的乘方，也具有这一性质，如(abc)n＝anbncn ‎(2)a，b与前面几个公式一样，可以表示具体的数，也可以表示一个代数式 例1 计算：‎ ‎(1)(5m )3； (2)(-xy2)3； ‎ ‎ 巩固练习 ‎1.P55 练一练2‎ ‎2.例2 计算：‎ ‎(1)(3xy2)2； (2)(-2ab3c2)4 解：(1)(3xy2)2=32·x2·(y2)2=9x2y4;‎ ‎(2)(-2ab3c2)4 =(-2)4·a4·(b3)4·(c2)4=16a4b12c8.‎ 解：(1)(5m)3＝53·m3＝125m3； ‎ ‎(2)(- xy2)3＝(-1)3·x3·(y2)3＝-x3y6.‎ ‎(1)系数的乘方；(2)因数中若有幂的形式，要注意运算步骤，先进行积的乘方，后作因数幂的乘方 板书设计 情境创设 ‎1、‎ ‎2、‎ 例1： ‎ 例2： ‎ 习题 作业布置 课后随笔 课时编号 ‎4‎ 备课时间 4‎