2017-2018学年湖南省涟源市七年级下学期期末考试数学试题含答案 8页

涟源市2017-2018学年下学期期末考试七年级试题 数 学 时量：120分钟          满分：120分 题号[来源:Z*xx*k.Com]‎ 一 二 三 总分 得分 一、选择题（共12小题，每小题3分，共36分）‎ ‎1．方程x-3y=1，xy=2，x-(1/y)=1，x-2y+3z=0，x2+y=3中是二元一次方程的有（A） ‎ A．1个 B．2个 C．3个 D．4个 ‎ ‎ ‎2．化简(-a2)·a5所得的结果是（B）‎ A．a7‎ B．-a7‎ C．a10‎ D．-a10‎ ‎ ‎ ‎3．一组数据按从小到大的顺序排列为1、2、3、x、4、5，若这组数据的中位数为3，则这组数据的方差是（D）‎ A．1‎ B．4/3‎ C．3/2‎ D．5/3‎ ‎ ‎ ‎4．方程2x-3y=7，用含x的代数式表示y为（B）‎ A．y=(7-2x)/3‎ B．y=(2x-7)/3‎ C．x=(7+3y)/2‎ D．x=(7-3y)/2‎ ‎ ‎ ‎5．用白铁皮做罐头盒，每张铁皮可制盒身25个，或制盒底40个，一个盒身与两个盒底配成一套罐头盒，现在有36张白铁皮，设用x张制作盒身，y张制作盒底可以使盒身和盒底正好配套，则所列方程组正确的是（B）‎ A．{x+y=36，25x=40y}‎ B．{x+y=36，2×25x=40y}‎ C．{x+y=36，25x=2×40y}‎ D．{x+y=36，40x=25y}‎ ‎ ‎ ‎6．若x+y=7，xy=-11，则x2+y2的值是（D）‎ A．49‎ B．27‎ C．38‎ D．71‎ ‎ ‎ ‎7．把x2y-2y2x+y3分解因式正确的是（C）‎ A．y(x2-2xy+y2)‎ B．x2y-y2(2x-y)‎ C．y(x-y)2‎ D．y(x+y)2‎ ‎ ‎ ‎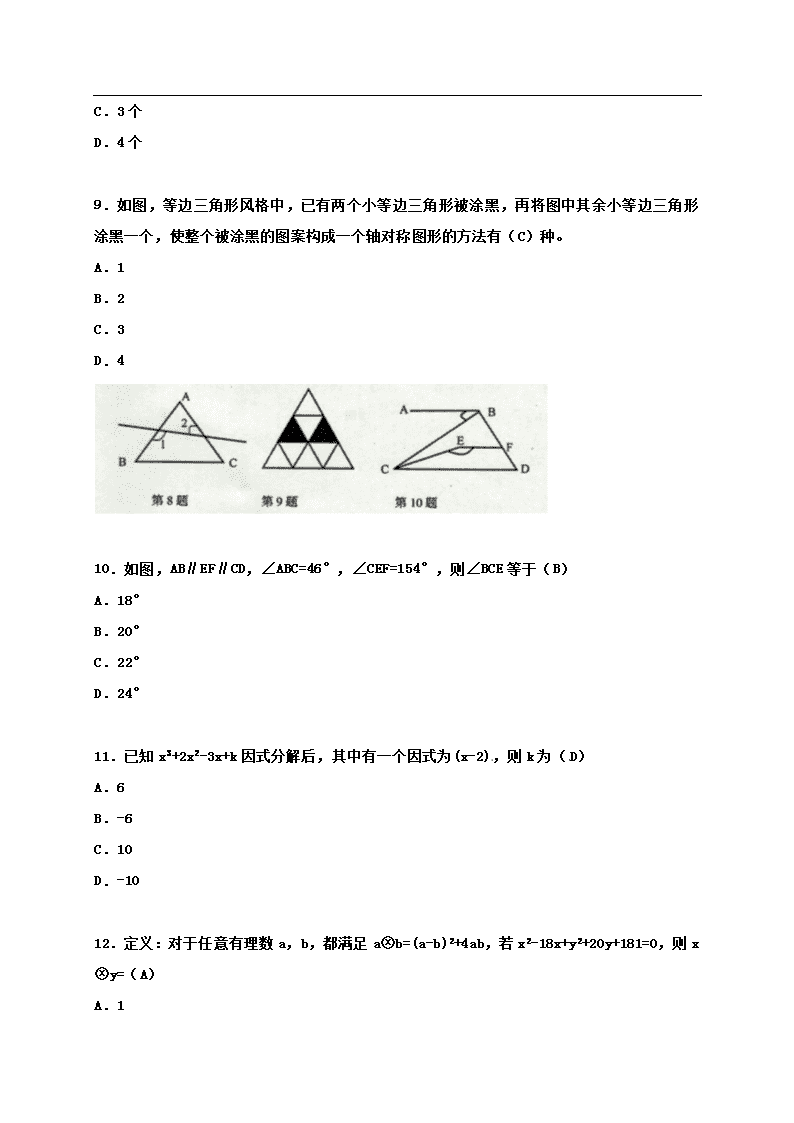8．如图所示，下列说法中：①∠A与∠B是同旁内角；②∠2与∠1是内错角；③∠A与∠C是内错角；④∠A与∠1是同位角。正确的个数是（C）‎ A．1个 B．2个 C．3个 D．4个 ‎ ‎ ‎9．如图，等边三角形风格中，已有两个小等边三角形被涂黑，再将图中其余小等边三角形涂黑一个，使整个被涂黑的图案构成一个轴对称图形的方法有（C）种。‎ A．1‎ B．2‎ C．3‎ D．4‎ ‎ [来源:Zxxk.Com]‎ ‎10．如图，AB∥EF∥CD，∠ABC=46°，∠CEF=154°，则∠BCE等于（B）‎ A．18°‎ B．20°‎ C．22°‎ D．24°‎ ‎ ‎ ‎11．已知x3+2x2-3x+k因式分解后，其中有一个因式为(x-2)，则k为（D）‎ A．6‎ B．-6‎ C．10‎ D．-10‎ ‎ ‎ ‎12．定义：对于任意有理数a，b，都满足aⓧb=(a-b)2+4ab，若x2-18x+y2+20y+181=0，则xⓧy=（A）‎ A．1‎ B．-1‎ C．361‎ D．-361‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A B D B B D C C C B D[来源:学科网ZXXK]‎ A 二、填空题（本题共6个小题，每题3分，共18分）‎ ‎13．20152-2014×2016=  1  .‎ ‎14．如果(x-2)(x+3)=x2+px-6，则p=  1  .‎ ‎15．已知多项式x2-mx+(1/4)是完全平方式，则m的值为 ±1  .‎ ‎16．若x=2，y=-3是方程组{x+y=m，2x-y=n}的解，则m+n=  6  .‎ ‎17．已知a2m=3，b3n=2，则(1/9)a4mb6n的值为   4  .‎ ‎18．已知m2+m-1=0，则m3+2m2+1= 2  .‎ 三、解答题（本题共66分）‎ ‎19．（每题4分，共8分）计算：‎ ‎（1）0.1259×(-8)10+(2/5)11×(5/2)12‎ ‎（2）(2x-2)(x+1)-(x-1)2-(x+1)2‎ 解：（1）原式=(1/8)9×89×8＋(2/5)11×(5/2)11×(5/2)‎ ‎                      =8＋(5/2)=10.5‎ ‎（2）原式=2x2-2-x2＋2x-1-x2-2x-1=-4‎ ‎ ‎ ‎20．（每题4分，共8分）解二元一次方程组：‎ ‎（1）{3x-4y=10，x+3y=-1}‎ ‎（2）{3(x-1)=y+5，(x+2)/2=(y-1)/3+1}‎ ‎ ‎ 解：（1）：在方程x+3y=-1两边同时乘以3得 ‎3x+9y=-3，用此方程减3x-4y=10得13y=-13‎ 所以可得y=-1‎ 将y=-1代入方程x+3y=-1得x=2‎ 因此原方程组的解为{x=2，y=-1}‎ ‎ ‎ ‎（2）：在方程(x+2)/2=(y-1)/3+1两边同时乘以6得 ‎3x+6=2y-2+6，整理得3x-2y=-2‎ 将方程3(x-1)=y+5整理变形可得3x-y=8‎ 用方程3x-y=8去减方程3x-2y=-2两边 可解得y=10‎ 把y=10代入方程3x-y=8得x=6[来源:学,科,网Z,X,X,K]‎ 因此原方程组的解为{x=6，y=10}‎ ‎ ‎ ‎21．（6分）如图，已知EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD（请填空）‎ 解：因为EF∥AD 所以∠2=  ∠3  （  两直线平等，同位角相等  ）‎ 又因为∠1=∠2‎ 所以∠1=∠3（  等量代换  ）‎ 所以AB∥  DG （  内错角相等，两直线平等  ）‎ 所以∠BAC+  ∠AGD  =180°（  两直线平等，同旁内角互补  ）‎ 因为∠BAC=70°（  已知 ）‎ 所以∠AGD=  180°-70°=110°（  等量代换  ）‎ ‎ ‎ ‎22．（6分）如图所示，不用量角器，将方格纸中的四边形绕着点O按逆时针方向旋转90°，画出旋转后的图形。（不用定过程，直接画出图形即可）‎ ‎ ‎ ‎23．（9 分）在解方程组{ax+5y=-17，4x-by=1}时，由于粗心，甲看错了方程组中的a，而得到解为{x=4，y=3}，乙看错了方程组中的b，而得到解为{x=-3，y=-1}。‎ ‎（1）求正确的a，b的值；‎ ‎（2）求原方程组的解。‎ 解：（1）：将{x=4，y=3}代入方程4x-by=1得b=5‎ 将{x=-3，y=-1}代入方程ax+5y=-17得a=4‎ ‎ ‎ ‎（2）：将a=4，b=5代入原方程组得 ‎{4x+5y=-17，4x-5y=1}‎ 解此方程组得{x=-2，y=-1.8}‎ ‎ ‎ ‎24．（9分）甲 ，乙两支仪仗队队员的身高（单位：cm）如下：‎ 甲队：178，177，179，178，177，178，177，179，178，179；‎ 乙队：178，179，176，178，180，178，176，178，177，180；‎ ‎（1）将下表填完整：‎ 身高 ‎176‎ ‎177‎ ‎178‎ ‎179[来源:学+科+网]‎ ‎180‎ 甲队（人数）‎ ‎0‎ ‎3‎ ‎4‎ ‎3‎ ‎0[来源:学科网ZXXK]‎ 乙队（人数）‎ ‎2[来源:学_科_网Z_X_X_K]‎ ‎1‎ ‎4‎ ‎1‎ ‎2‎ ‎（2）甲队队员身高的平均数为  178 cm，乙队队员身高的平均数为  178  cm；‎ ‎（3）你认为哪支仪仗队更为整齐？简要说明理由。‎ 甲队方差：[(178-178)2+(177-178) 2+(179-178)2+(178-178) 2 +(177-178) 2 +(178-178) 2 +(177-178)2 +(179-178) 2 +(178-178) 2 +(179-178) 2]/10=[0+1+1+0+1+0+1+1+0+1]/10=0.6‎ 乙队方差：[(178-178)2+(179-178) 2+(176-178)2+(178-178) 2 +(180-178) 2 +(178-178) 2 +(176-178)2 +(178-178) 2 +(177-178) 2 +(180-178) 2]/10=[0+1+4+0+4+0+4+0+1+4]/10=1.8‎ 答：甲队更加整齐。原因：甲队身高的方差为0.6，乙队身高的方差为1.8，甲队的方差较小。‎ ‎ ‎ ‎25．（10分）某超市为了促销，对A、B两种商品进行打折出售。打折前，购买5件A商品和2件B商品需要88元，购买7件A商品和3件B商品需要124元。促销期间，购买100件A商品和100件B商品仅需1500元。‎ ‎（1）求打折前每件A商品和B商品的价格。‎ ‎（2）若B商品所打折扣为7.5折，求促销期间每件A商品的价格。‎ 解：（1）设打折前A、B两种商品的单价分别为x元、y元，则 ‎{5x+2y=88，7x+3y=124}‎ 解得：{x=16，y=4}‎ ‎（2）设促销期间A商品的价格为z元，则 ‎100×4×0.75＋100z=1500‎ 解得：z=12‎ 答：打折前A商品每件16元，B商品每件4元。促销期间每件A商品的价格为12元。‎ ‎ ‎ ‎26．（10分）如图1，直线AG与直线BH和DI分别相交于点A和点G，点C为DI上一点，且CD⊥AG，垂足为点E，∠DCE-∠HAE=90°。‎ ‎（1）求证：BH∥DI。‎ ‎（2）如图2：直线AF交DC于，AM平分∠EAF，AN平分∠BAE，证明：∠AFG＝２∠MAN 证明：（1）：∠DCE＋∠ECG=180°‎ ‎∠CEG＋∠CGA＋∠ECG=180°‎ 所以∠DCE=∠CEG＋∠CGA 因为CD⊥AG 所以∠DCE－∠CGA=∠CEG=90°‎ 又因为∠DCE－∠HAE=90°‎ 所以∠CGA=∠HAE 所以BH∥DI ‎ ‎ ‎（2）：因为AM平分∠EAF  AN平分∠BAE 所以∠EAM=∠FAM  ∠EAN=∠BAN 又因为∠MAN=∠EAN－∠EAM 所以∠MAN=∠BAN－∠FAM 又因为∠BAN=∠BAF＋∠FAN ‎∠FAM=∠MAN＋∠FAN 所以∠MAN=∠BAF－∠MAN 所以∠BAF=2∠MAN 又所以BH∥DI 所以∠AFG=∠BAF 所以∠AFG=2∠MAN