2019-2020学年初二上学期月考数学试题（福建省莆田青璜中学） 2页

青璜中学八年级数学 10 月月考试卷 一、精心选一选：让你算的少，要你想的多，只选一个可要认准哦！本大题共 10 小题， 每小题 4 分，共 40 分。 1．若一个三角形的两边长分别是 4、9，则这个三角形的第三边的长可能是（ ） A．3 B．5 C．8 D．13 2．若 AD 是△ABC 的中线，则下列结论正确的是（ ） A．BD＝CD B．AD⊥BC C．∠BAD＝∠CAD D．BD＝CD 且 AD⊥BC 3．在△ABC 中，若满足下列条件，则一定不是直角三角形的是（ ） A．∠A＝∠B+∠C B．∠A＝∠C﹣∠B C．一个外角等于与它相邻的内角 D．∠A：∠B：∠C＝1：3：5 4．在△ABC 中，如果∠B﹣2∠C＝90°﹣∠C，那么△ABC 是（ ） A．直角三角形 B．钝角三角形 C．锐角三角形 D．锐角三角形或钝角三角形 5．一个正多边形，它的每一个外角都等于 40°，则该正多边形是（ ） A．正六边形 B．正七边形 C．正八边形 D．正九边形 6．将一个多边形纸片沿一条直线剪下一个三角形后，变成一个六边形，则原多边形纸片的边数不 可能是（ ） A．5 B．6 C．7 D．8 *7．如果一个三角形两边上的高的交点在三角形的内部，那么这个三角形是（ ） （本题来源于校本作业作业 2 第 3 题） A．锐角三角形 B．直角三角形 C．钝角三角形 D．任意三角形 *8．下列各组图形中，一定全等的是（ ）（本题来源于课课练第 23 页第 3 题） A．各有一个角是 45°的两个等腰三角形 B．腰和顶角都相等的两个等腰三角形 C．各有一个角是 40°，腰长都为 3 的两个等腰三角形 D．两个等边三角形 9．如图，△ABC 中，∠1＝∠2，G 为 AD 中点，延长 BG 交 AC 于 E， F 为 AB 上一点，且 CF⊥AD 于 H，下列判断，其中正确的个数是（ ） ① BG 是△ABD 中边 AD 上的中线； ② AD 既是△ABC 的角平分线，也是△ABE 的角平分线； ③ CH 既是△ACD 中 AD 边上的高线，也是△ACH 中 AH 边上的高线． A．0 B．1 C．2 D．3 10．如图，在△OAB 和△OCD 中，OA＝OB，OC＝OD，OA＞OC，∠OCD=∠ODC， ∠OAB=∠OBA，OE⊥AC，OF⊥BD，∠AOB＝∠COD＝40°，连接 AC，BD 交于点 M，连接 OM．下列结论： ① AC＝BD； ② ∠AMB＝40°； ③ OM 平分∠BOC； ④ MO 平分∠BMC．其中 正确的个数为（ ） A．4 B．3 C．2 D．1 二、细心填一填：简洁的结果，需要的是细心！本大题共 6 小题，每小题 4 分，共 24 分。 11．如果 n 边形的每一个内角都等于与它相邻外角的 2 倍，则 n 的值是 ． 12．在△ABC 中，∠ACB＝60°，CE 为△ABC 的角平分线，AC 边上的高 BD 与 CE 所在的直线交 于点 F，若∠ABD：∠ACF＝2：3，则∠BEC 的度数为 ． 13．如图，在△ABC 中，AD 是 BC 边上的高，AE 平分∠BAC，∠B＝∠BCA﹣70°，∠DAE= °． 第 13 题 第 14 题 第 16 题 14．如图所示，点 A、B、C、D 在同一条直线上，△ACF≌△DBE，AD＝10cm，BC＝6cm， 则 AB 的长为 cm． *15．锐角△ABC 中，∠B=3∠C，则∠C 的取值范围是 （本题来源于校本作业作业 4 第 8 题） 16．如图，在 Rt△ABC 中，∠ACB=90°，AC=BC，∠CAB=45°，D 为 BC 上一点，CE⊥AD 于 点 E，延长 CE 交 AB 于点 F，BG⊥CB 于点 B，∠ADC=45°+∠DCE.则  DE CEAD 2 . 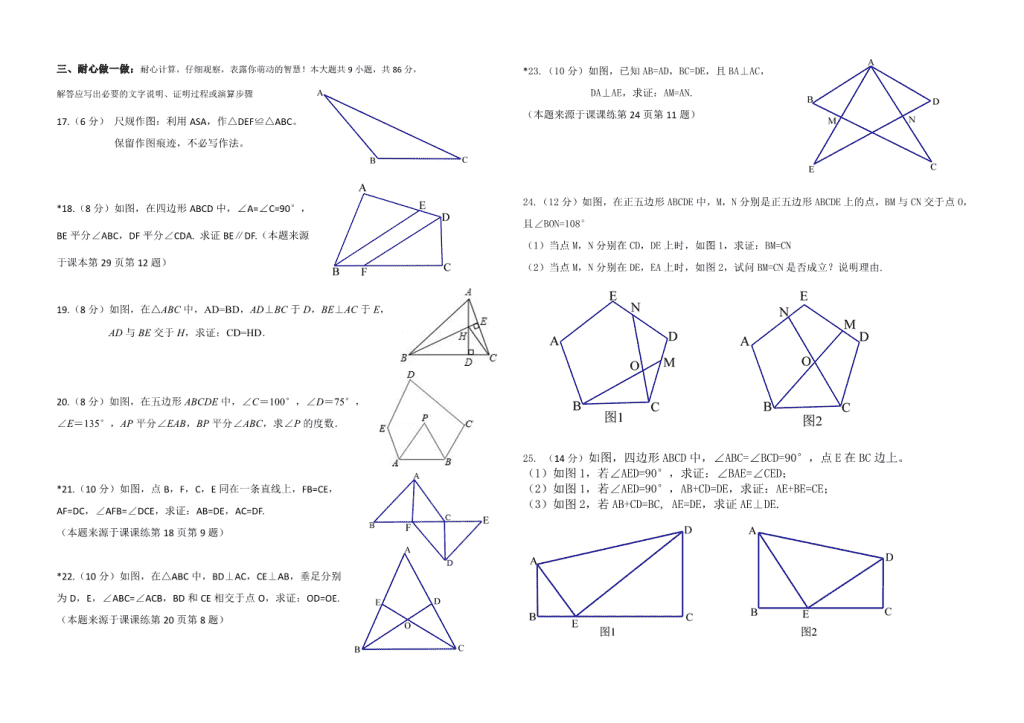第 9 题 三、耐心做一做：耐心计算，仔细观察，表露你萌动的智慧！本大题共 9 小题，共 86 分， 解答应写出必要的文字说明、证明过程或演算步骤 17.（6 分） 尺规作图：利用 ASA，作△DEF≌△ABC。 保留作图痕迹，不必写作法。 *18.（8 分）如图，在四边形 ABCD 中，∠A=∠C=90°， BE 平分∠ABC，DF 平分∠CDA. 求证 BE∥DF.（本题来源 于课本第 29 页第 12 题） 19.（8 分）如图，在△ABC 中，AD=BD，AD⊥BC 于 D，BE⊥AC 于 E， AD 与 BE 交于 H，求证：CD=HD． 20.（8 分）如图，在五边形 ABCDE 中，∠C＝100°，∠D＝75°， ∠E＝135°，AP 平分∠EAB，BP 平分∠ABC，求∠P 的度数． *21.（10 分）如图，点 B，F，C，E 同在一条直线上，FB=CE， AF=DC，∠AFB=∠DCE，求证：AB=DE，AC=DF. （本题来源于课课练第 18 页第 9 题） *22.（10 分）如图，在△ABC 中，BD⊥AC，CE⊥AB，垂足分别 为 D，E，∠ABC=∠ACB，BD 和 CE 相交于点 O，求证：OD=OE. （本题来源于课课练第 20 页第 8 题） *23.（10 分）如图，已知 AB=AD，BC=DE，且 BA⊥AC， DA⊥AE，求证：AM=AN. （本题来源于课课练第 24 页第 11 题） 24.（12 分）如图，在正五边形 ABCDE 中，M，N 分别是正五边形 ABCDE 上的点，BM 与 CN 交于点 O， 且∠BON=108° （1）当点 M，N 分别在 CD，DE 上时，如图 1，求证：BM=CN （2）当点 M，N 分别在 DE，EA 上时，如图 2，试问 BM=CN 是否成立？说明理由. 25. （14 分）如图，四边形 ABCD 中，∠ABC=∠BCD=90°，点 E 在 BC 边上。 （1）如图 1，若∠AED=90°，求证：∠BAE=∠CED； （2）如图 1，若∠AED=90°，AB+CD=DE，求证：AE+BE=CE； （3）如图 2，若 AB+CD=BC, AE=DE，求证 AE⊥DE.