三角形的内角和教案(2) 7页

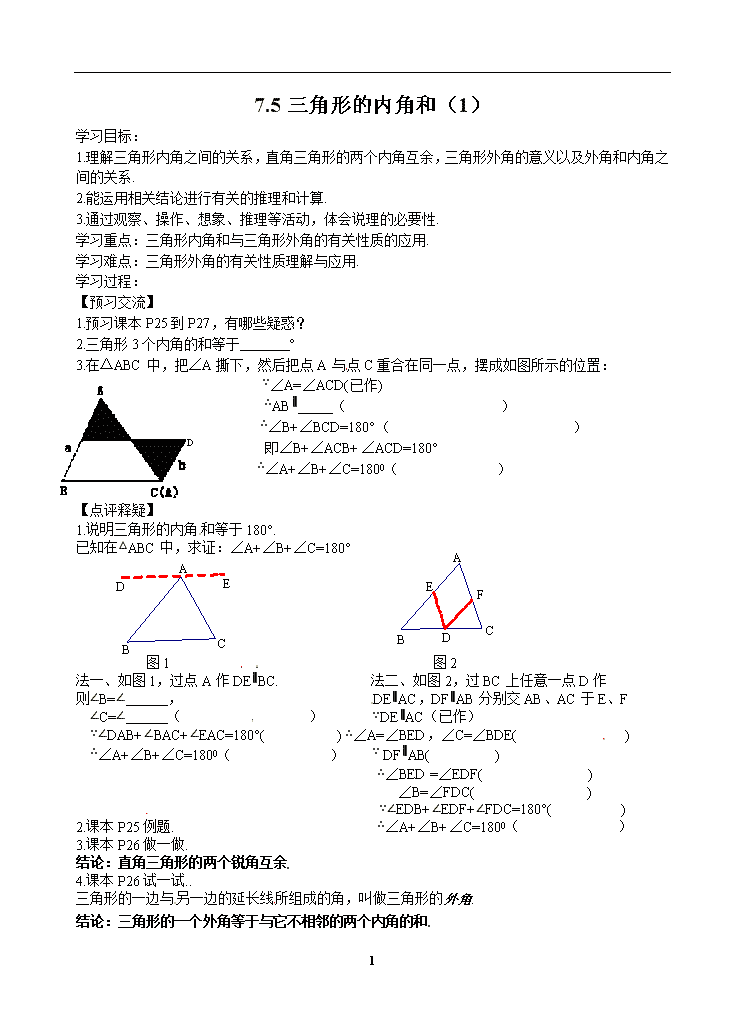
‎ ‎ ‎7.5三角形的内角和（1）‎ 学习目标：‎ ‎1.理解三角形内角之间的关系，直角三角形的两个内角互余，三角形外角的意义以及外角和内角之间的关系.‎ ‎2.能运用相关结论进行有关的推理和计算.‎ ‎3.通过观察、操作、想象、推理等活动，体会说理的必要性.‎ 学习重点：三角形内角和与三角形外角的有关性质的应用.‎ 学习难点：三角形外角的有关性质理解与应用.‎ 学习过程：‎ ‎【预习交流】‎ ‎1.预习课本P25到P27，有哪些疑惑？‎ ‎2.三角形3个内角的和等于 °‎ ‎3.在△ABC中，把∠A撕下，然后把点A与点C重合在同一点，摆成如图所示的位置：‎ ‎ ∵∠A=∠ACD(已作)‎ ‎ ∴AB∥ （ ）‎ ‎∴∠B+∠BCD=180°（ ）‎ ‎ 即∠B+∠ACB+∠ACD=180°‎ ‎ ∴∠A+∠B+∠C=1800（ ）‎ ‎【点评释疑】‎ ‎1.说明三角形的内角和等于180°.‎ 已知在△ABC中，求证：∠A+∠B+∠C=180°‎ ‎ 图1 图2‎ 法一、如图1，过点A作DE∥BC. 法二、如图2，过BC上任意一点D作 则∠B=∠ ， DE∥AC，DF∥AB分别交AB、AC于E、F ‎∠C=∠ （ ） ∵DE∥AC（已作）‎ ‎∵∠DAB+∠BAC+∠EAC=180°( ) ∴∠A=∠BED，∠C=∠BDE( )‎ ‎∴∠A+∠B+∠C=1800（ ） ∵ DF∥AB( )‎ ‎ ∴∠BED =∠EDF( )‎ ‎∠B=∠FDC( )‎ ‎ ∵∠EDB+∠EDF+∠FDC=180°( )‎ ‎2.课本P25例题. 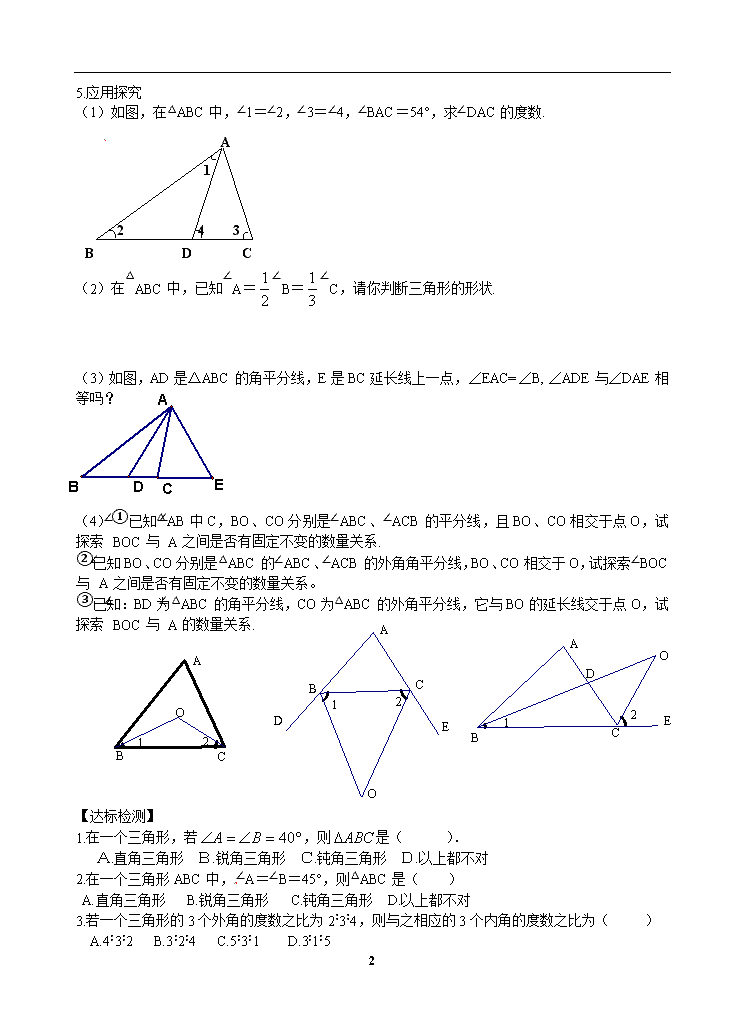∴∠A+∠B+∠C=1800（ ）‎ ‎3.课本P26做一做.‎ 结论：直角三角形的两个锐角互余.‎ ‎4.课本P26试一试..‎ 三角形的一边与另一边的延长线所组成的角，叫做三角形的外角.‎ 结论：三角形的一个外角等于与它不相邻的两个内角的和.‎ 7‎ ‎ ‎ ‎5.应用探究 B　　　　　　 D　 C ‎2　　　　　 4　 3 ‎ ‎1　　　　 ‎ A　　　　 ‎ ‎（1）如图，在△ABC中，∠1＝∠2，∠3＝∠4，∠BAC＝54°，求∠DAC的度数.‎ ‎（2）在△ABC中，已知∠A＝∠B＝∠C，请你判断三角形的形状.‎ ‎（3）如图，AD是△ABC的角平分线，E是BC延长线上一点，∠EAC=∠B, ∠ADE与∠DAE相等吗？‎ ‎（4）①已知△AB中C，BO、CO分别是∠ABC、∠ACB的平分线，且BO、CO相交于点O，试探索∠BOC与∠A之间是否有固定不变的数量关系.‎ ‎②已知BO、CO分别是△ABC的∠ABC、∠ACB的外角角平分线，BO、CO相交于O，试探索∠BOC与∠A之间是否有固定不变的数量关系。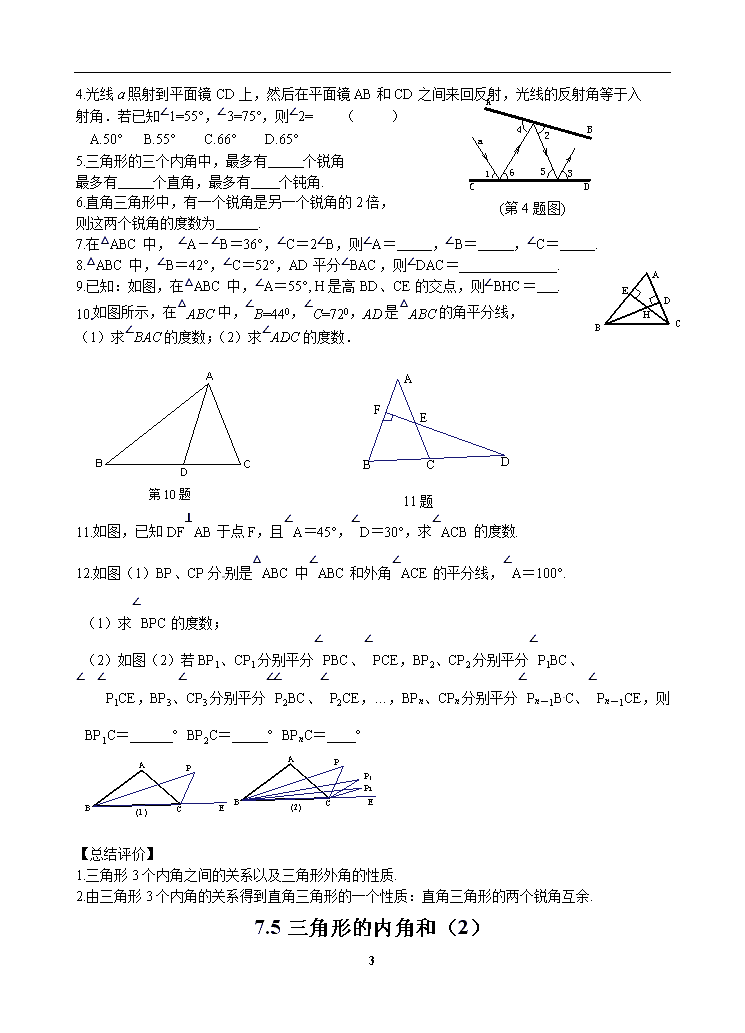‎ ‎③已知：BD为△ABC的角平分线，CO为△ABC的外角平分线，它与BO的延长线交于点O，试探索∠BOC与∠A的数量关系.‎ ‎【达标检测】‎ ‎1.在一个三角形，若，则是（ ）．‎ Ａ.直角三角形 Ｂ.锐角三角形 Ｃ.钝角三角形 Ｄ.以上都不对 ‎2.在一个三角形ABC中，∠A＝∠B＝45°，则△ABC是（ ）‎ A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上都不对 ‎3.若一个三角形的3个外角的度数之比为2∶3∶4，则与之相应的3个内角的度数之比为（ ）‎ A.4∶3∶2 B.3∶2∶4 C.5∶3∶1 D.3∶1∶5‎ 7‎ ‎ ‎ ‎4.光线a照射到平面镜CD上，然后在平面镜AB和CD之间来回反射，光线的反射角等于入 射角．若已知∠1=55°，∠3=75°，则∠2= （ ）‎ A.50° B.55° C.66° D.65°‎ ‎5.三角形的三个内角中，最多有 个锐角 最多有 个直角，最多有 个钝角.‎ ‎(第4题图)‎ ‎6.直角三角形中，有一个锐角是另一个锐角的2倍，‎ 则这两个锐角的度数为 .‎ ‎7.在△ABC中， ∠A－∠B＝36°，∠C＝2∠B，则∠A＝ ，∠B＝ ，∠C＝ .‎ ‎8.△ABC中，∠B＝42°，∠C＝52°，AD平分∠BAC，则∠DAC＝______________.‎ ‎9.已知：如图，在△ABC中，∠A＝55°, H是高BD、CE的交点，则∠BHC＝ . ‎ ‎10.如图所示，在△ABC中，∠B=440，∠C=720，AD是△ABC的角平分线，‎ ‎（1）求∠BAC的度数；（2）求∠ADC的度数． ‎ 第10题 ‎ 11题 ‎11.如图，已知DF⊥AB于点F，且∠A＝45°，∠D＝30°，求∠ACB的度数.‎ ‎12.如图（1）BP、CP分别是△ABC中∠ABC和外角∠ACE的平分线，∠A＝100°.‎ ‎ （1）求∠BPC的度数；‎ ‎ （2）如图（2）若BP1、CP1分别平分∠PBC、∠PCE，BP2、CP2分别平分∠P1BC、‎ ‎ ∠P1CE，BP3、CP3分别平分∠P2BC、∠P2CE，…，BPn、CPn分别平分∠Pn－1BC、∠Pn－1CE，则∠BP1C＝ °∠BP2C＝ °∠BPnC＝ °‎ ‎ ‎ ‎【总结评价】‎ ‎1.三角形3个内角之间的关系以及三角形外角的性质.‎ ‎2.由三角形3个内角的关系得到直角三角形的一个性质：直角三角形的两个锐角互余.‎ ‎7.5三角形的内角和（2）‎ 7‎ ‎ ‎ 学习目标：‎ ‎1.通过将多边形分割成三角形，从而探索出多边形内角和的计算公式，并能进行应用.‎ ‎2.经历操作、探索等活动，提高分析问题、解决问题的水平，提升从不同角度思考问题的能力.‎ 学习重点：理解多边形的内角和公式的推导过程，体会化归思想.‎ 学习难点：从不同角度思考问题.‎ 导学过程：‎ ‎【预习交流】‎ ‎1.预习课本P27到P28，记下你的疑惑.‎ ‎2.在△ABC中，如果∠A=2∠B=3∠C，则△ABC 是 （按角分）三角形.‎ ‎3.如图是一个五角星，则∠A+∠B+∠C+∠D+∠E= ° 3题图 4题图 ‎4. 如图，∠A+∠B+∠C+∠D+∠E= °‎ ‎5.直角三角形的两个锐角平分线所夹的钝角= °‎ ‎6.在△ABC中， ∠A－∠B＝36°，∠C＝2∠B，则∠A＝　　　，∠B＝　　　，∠C＝　　　.‎ ‎7.一个零件的形状如图中阴影部分．按规定∠A应等于90º，∠B、∠C应分别是29º和21º，检验 第7题图 人员度量得∠BDC＝141º，就断定这个零件不合格．你能说明理由吗？ ‎ ‎8.如图，已知△ABC中，已知∠B＝65°，∠C＝45°，AD是BC边上的高，AE是∠BAC的平分线，求∠DAE的度数.‎ ‎【点评释疑】‎ ‎1. 课本P27议一议.‎ 结论：n边形的内角和为（n-2）·180°.‎ ‎2. 课本P28想一想.‎ ‎3.应用探究 ‎（1）一个多边形的内角和是2340°，求它的边数.‎ ‎（2）一个多边形的各个内角都相等，且一个内角是150°，你知道它是几边形吗？‎ ‎（3）一个五边形截去一个角后，求剩下的多边形的内角和.‎ 7‎ ‎ ‎ ‎（4）一个多边形，除去一个内角外，其余各内角的和为2750°，求这个多边形的边数.‎ ‎（5）如图，求∠1＋∠2＋∠3＋∠4的度数．‎ ‎【达标检测】 ‎ ‎1.多边形的内角和可能是（ ）A.810° B.540° C.180° D.605°‎ ‎2.如果一个四边形的一组对角都是直角，那么另一组对角可以（ ）‎ Ａ.都是锐角 B.都是钝角 C.是一个锐角和一个直角 D.是一个锐角和一个钝角 ‎3.一个多边形的边数增加1，则它的内角和将（ ）Ａ.增加90° B.增加180° C.增加360° D.不变 ‎4.多边形内角和增加360°，则它的边数（ ）Ａ.增加1 B.增加2 C.增加3 D.不变 ‎5.若一个多边形的对角线有14条，则这个多边形的边数是（ ）A.10 B.7 C.14 D.6‎ ‎6.一个十边形所有内角都相等，它的每一个内角等于 .‎ ‎7.如图，在四边形ABCD中，∠1、∠2分别是∠BCD和∠BAD的补角，‎ 且∠B＋∠ADC＝140°，则∠1＋∠2＝ °.‎ ‎8.已知九边形中，除了一个内角外，其余各内角之和是1205°，求该内角.‎ ‎9.将纸片△ABC沿DE折叠使点A落在A’处的位置.‎ ‎（1）如果A’落在四边形BCDE的内部（如图1），∠A’与∠1＋∠2之间存在怎样的数量关系？并说明理由.‎ ‎（2）如果A’落在四边形BCDE的的BE边上，这时图1中的∠1变为0°角，则∠A’与∠2之间的关系是 .‎ ‎（3）如果A’落在四边形BCDE的外部（如图2），这时∠A’与∠1、∠2之间又存在怎样的数量关系？并说明理由. ‎ ‎【总结评价】‎ ‎1．多边形内角和公式.‎ ‎2．探求多边形内角和公式的方法.‎ ‎7.5三角形的内角和（3）‎ 学习目标：‎ 7‎ ‎ ‎ ‎1.知道多边形的外角的含义，并能在图形中加以识别.‎ ‎2.知道多边形的外角和的结论，并能用来进行有关的计算和推理.‎ 学习重点：掌握多边形外角和的特点.‎ 学习难点：多边形外角和性质的应用.‎ 学习过程：‎ ‎【预习交流】‎ ‎1.预习课本P29到P30，有哪些疑惑？‎ ‎2.五边形的内角和是__________，六边形的内角和是_________.‎ ‎3.若一个多边形的内角和等于1260°，则这个多边形是　　　边形.‎ ‎4.如果一个多边形的每一个内角都等于108°，则这个多边形是　　　边形.‎ ‎5.在四边形ABCD中，若∠A＝∠C＝90°，2∠B＝3∠D，则∠B＝ °，∠D＝ °.‎ 第6题图 ‎6.如图，在四边形ABCD中，∠1=∠2，∠3=∠4，且∠D+∠C=220°，‎ 求∠AOB的度数．‎ ‎【点评释疑】‎ ‎1.多边形的一边与另一边的延长线的夹角，叫做多边形的外角.‎ 在每个顶点处分别取这个多边形的一个外角，这些外角的和叫做这个多边形的外角和.‎ ‎2.课本P29做一做.‎ 结论：任意多边形的外角和等于360°.‎ ‎3.课本P30议一议.‎ ‎4.应用探究 ‎（1）一个多边形的内角和与外角和相等，这个多边形是几边形？‎ ‎（2）一个多边形每个外角都是60°，求这个多边形的边数.‎ ‎（3）一个正多边形的每一个内角都比相邻的外角大36°，求这个多边形的边数.‎ ‎（4）如图，求∠A+∠B+∠C+∠D+∠E+∠F的度数.‎ ‎【课堂检测】 ‎ ‎1.一个多边形，它的内角和是外角和的2倍，这个多边形的边数是（ ）．‎ 7‎ ‎ ‎ A.3 B.4 C.5 D.6‎ ‎2.一个多边形，它的每个内角都等于相邻外角的5倍， 则这个多边形是( )‎ ‎ A.五边形 B.十边形 C.十二边形 D.不存在 ‎3.用正方形地砖铺地面时，在一个交接点周围的正方形的个数为（ ）‎ ‎ A.2 B.3 C.4 D.5‎ ‎4.n边形的内角和等于 ，多边形的外角和都等于 .‎ ‎5.一个多边形的每个外角都是300， 则这个多边形是 边形．‎ ‎6.一个五边形五个外角的比是2：3：4：5：6，则这个五边形五个外角的度数分别是 .‎ ‎7.多边形边数增加一条，则它的内角和增加 度，外角和 .‎ ‎8.一个多边形的外角中钝角的个数最多只能有 个.‎ ‎9.如图，若AB∥CD，EF与AB、CD分别相交于点E、F，EP⊥EF，∠EFD 的平分线与EP相交于点P，且∠BEP=40°，则∠EPF=_______度．‎ 图10‎ ‎10.如图，分别以边形的顶点为圆心，以单位1为半径画圆，则图中阴影部分的面积之和为 个平方单位．‎ ‎11.一个多边形的外角和是内角和的，它是几边形？ ‎ ‎12.一个多边形的每一个外角都相等，且每一个内角都比外角大900，求这个多边形的边数和每个内角的度数.‎ ‎【总结评价】‎ ‎1.多边形的外角和的性质.‎ ‎2.综合、对比所学，形成理性思维，有条理地表达.‎ 7‎