2014-2015 学年重庆七十一中七年级（上）月考数学试卷（12 月 份） 16页

‎2014-2015学年重庆七十一中七年级（上）月考数学试卷（12月份）‎ ‎　‎ 一．选择题 ‎1．在0，﹣2，1，6这四个数中，最小的数是（　　）‎ A．6 B．1 C．﹣2 D．0‎ ‎　‎ ‎2．如图是一个正方体的表面展开图，上面标有“我、爱、七、十、一、中”六个字，图中“爱”对面的字是（　　）‎ A．七 B．一 C．十 D．中 ‎　‎ ‎3．下列说法不正确的是（　　）‎ A．0既不是正数，也不是负数 B．互为相反数的两个数的和为0‎ C．互为倒数的两个数的和为1‎ D．0的绝对值是0‎ ‎　‎ ‎4．A为数轴上表示2的点，将点A沿数轴向左平移7个单位到点B，再由B向右平移6个单位到点C，则点C所表示的数是（　　）‎ A．11 B．1 C．2 D．3‎ ‎　‎ ‎5．在﹣，﹣|12|，﹣20，0，﹣（﹣5）中，负数的个数有（　　）‎ A．2个 B．3 个 C．4 个 D．5 个 ‎　‎ ‎6．如图所示，关于线段、射线和直线的条数，下列说法正确的是（　　）‎ A．五条线段，三条射线 B．一条直线，三条线段 C．三条线段，两条射线，一条直线 D．三条线段，三条射线 ‎　‎ ‎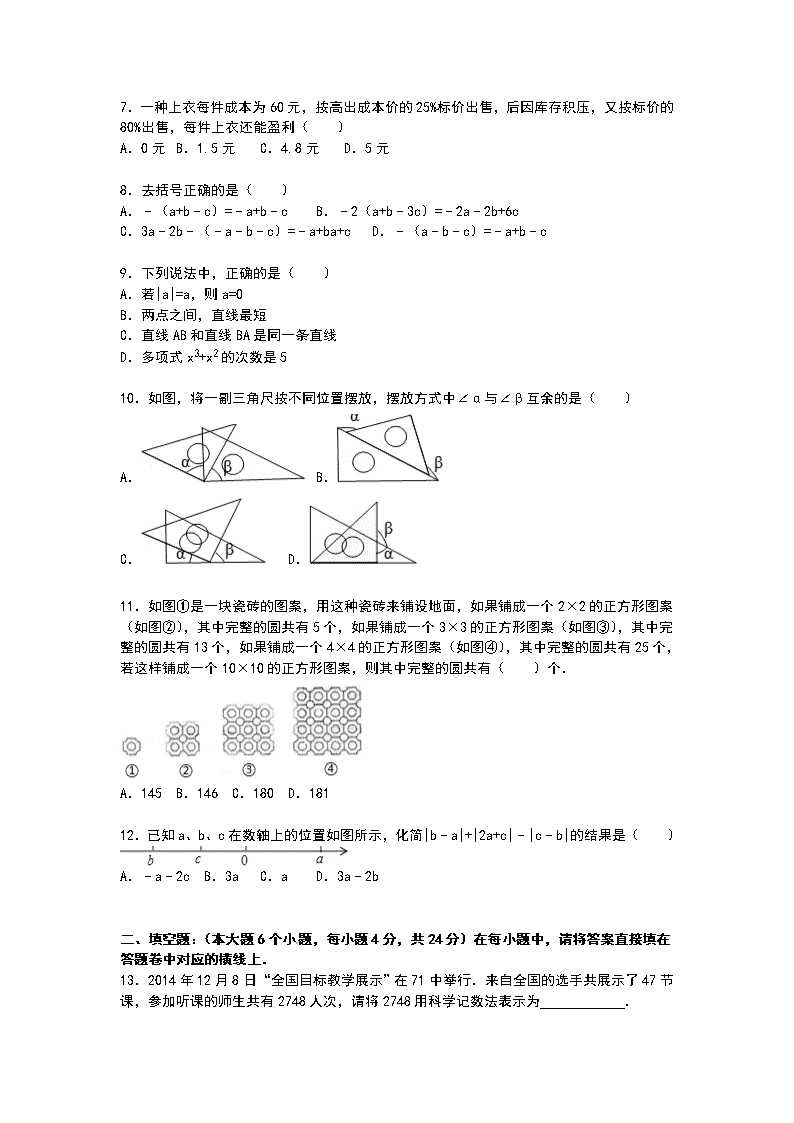7．一种上衣每件成本为60元，按高出成本价的25%标价出售，后因库存积压，又按标价的80%出售，每件上衣还能盈利（　　）‎ A．0元 B．1.5元 C．4.8元 D．5元 ‎　‎ ‎8．去括号正确的是（　　）‎ A．﹣（a+b﹣c）=﹣a+b﹣c B．﹣2（a+b﹣3c）=﹣2a﹣2b+6c C．3a﹣2b﹣（﹣a﹣b﹣c）=﹣a+ba+c D．﹣（a﹣b﹣c）=﹣a+b﹣c ‎　‎ ‎9．下列说法中，正确的是（　　）‎ A．若|a|=a，则a=0‎ B．两点之间，直线最短 C．直线AB和直线BA是同一条直线 D．多项式x3+x2的次数是5‎ ‎　‎ ‎10．如图，将一副三角尺按不同位置摆放，摆放方式中∠α与∠β互余的是（　　）‎ A． B． ‎ C． D．‎ ‎　‎ ‎11．如图①是一块瓷砖的图案，用这种瓷砖来铺设地面，如果铺成一个2×2的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个3×3的正方形图案（如图③），其中完整的圆共有13个，如果铺成一个4×4的正方形图案（如图④），其中完整的圆共有25个，若这样铺成一个10×10的正方形图案，则其中完整的圆共有（　　）个．‎ A．145 B．146 C．180 D．181‎ ‎　‎ ‎12．已知a、b、c在数轴上的位置如图所示，化简|b﹣a|+|2a+c|﹣|c﹣b|的结果是（　　）‎ A．﹣a﹣2c B．3a C．a D．3a﹣2b ‎　‎ ‎　‎ 二、填空题：（本大题6个小题，每小题4分，共24分）在每小题中，请将答案直接填在答题卷中对应的横线上．‎ ‎13．2014年12月8日“全国目标教学展示”在71中举行．来自全国的选手共展示了47节课，参加听课的师生共有2748人次，请将2748用科学记数法表示为　　　　　　．‎ ‎　‎ ‎14．单项式﹣πa2bc的系数是　　　　　　；次数是　　　　　　．‎ ‎　‎ ‎15．∠A=32°36′，它的补角为　　　　　　．‎ ‎　‎ ‎16．多项式5x2y+y3﹣3xy2﹣x3按x的降幂排列是　　　　　　．‎ ‎　‎ ‎17．已知代数式2a3bn+1与﹣3am﹣2b2是同类项，则2m+3n=　　　　　　．‎ ‎　‎ ‎18．观察下面一列有规律的数，根据这个规律可知第n个数是　　　　　　（n是正整数）‎ ‎　‎ ‎　‎ 三、解答题：（本大题2个小题，每小题7分，共14分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答书写在答题卷中对应的位置上．‎ ‎19．计算：‎ ‎（1）﹣7+13﹣6+20； ‎ ‎（2）．‎ ‎　‎ ‎20．作图题．如图，在同一平面内有四个点A、B、C、D，‎ ‎①画射线BD； ‎ ‎②画直线BC； ‎ ‎③连结AC与射线BD相交于点P；‎ ‎④延长线段AD与直线BC相交于点Q．‎ ‎　‎ ‎　‎ 四、解答题（每题10分，共40分）‎ ‎21．计算：‎ ‎（1）2（x2y+xy2）﹣3（x2y﹣5x）﹣2xy2﹣7x；‎ ‎（2）．‎ ‎　‎ ‎22．先化简，再求值：‎ 已知：（a+1）2+|b+2|=0，求代数式﹣a2b+（3ab2﹣a2b）﹣2（2ab2﹣a2b）的值．‎ ‎　‎ ‎23．如图，OE为∠AOD的平分线，∠COD=∠EOC，∠COD=15°，‎ 求：①∠EOC的大小； ②∠AOD的大小．‎ ‎　‎ ‎24．如图已知点C为AB上一点，AC=12cm，CB=AC，D、E分别为AC、AB的中点，求DE的长．‎ ‎　‎ ‎　‎ 四、解答题：（每小题12分，共24分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答书写在答题卷中对应的位置上 ‎25．重庆某餐饮集团公司将沙坪坝下属一个分公司对外招商承包，有符合条件的两个企业甲、乙，分别拟定上缴利润方案如下：‎ 甲：每年结算一次上缴利润，第一年上缴利润5万元，以后每年比前一年增加5万元；‎ 乙：每半年结算一次上缴利润，第一个半年上缴利润1.5万元，以后每半年比前一半年增加1.5万元；‎ ‎（1）如果企业乙承包一年，则需上缴的总利润为　　　　　　万元．‎ ‎（2）如果承包4年，你认为应该承包给哪家企业，总公司获利多？为什么？‎ ‎（3）如果承包n年，请你用含n的代数式分别表示两企业上缴利润的总金额（单位：万元）．‎ ‎　‎ ‎26．近年来，随着社会竞争的日益激烈，家长为使孩子不输在教育的起跑线上，不惜花费重金购置教育质量好的学区的房产．张先生准备购买一套小户型学区房，他去某楼盘了解情况得知，该户型的单价是12000元/m2，面积如图所示（单位：米，卫生间的宽未定，设宽为x米），售房部为张先生提供了以下两种优惠方案：‎ 方案一：整套房的单价是12000元/m2，其中厨房可免费赠送的面积；‎ 方案二：整套房按原销售总金额的9折出售．‎ ‎（1）用y1表示方案一中购买一套该户型商品房的总金额，用y2表示方案二中购买一套该户型商品房的总金额，分别求出两种方案中的总金额y1、y2（用含x的式子表示）；‎ ‎（2）求当x=2时，两种方案的总金额分别是多少元？‎ ‎（3）张先生因现金不够，在银行借了18万元住房贷款，贷款期限为6年，从开始贷款的下一个月起逐月偿还，贷款月利率是0.5%，每月还款数额=平均每月应还的贷款本金数额+月利息，月利息=上月所剩贷款本金数额×月利率．‎ ‎①张先生借款后第一个月应还款数额是多少元？‎ ‎②假设贷款月利率不变，若张先生在借款后第n（1≤n≤72，n是正整数）个月的还款数额为P，请写出P与n之间的关系式．‎ ‎　‎ ‎　‎ ‎2014-2015学年重庆七十一中七年级（上）月考数学试卷（12月份）‎ 参考答案与试题解析 ‎　‎ 一．选择题 ‎1．在0，﹣2，1，6这四个数中，最小的数是（　　）‎ A．6 B．1 C．﹣2 D．0‎ 考点： 有理数大小比较．‎ 分析： 先在数轴上表示出各数，再根据数轴的特点即可得出结论．‎ 解答： 解：如图所示，‎ ‎，‎ 由图可知，这四个数中，最小的数是﹣2．‎ 故选C．‎ 点评： 本题考查的是有理数的大小比较，熟知数轴上右边的数总比左边的大是解答此题的关键．‎ ‎　‎ ‎2．如图是一个正方体的表面展开图，上面标有“我、爱、七、十、一、中”六个字，图中“爱”对面的字是（　　）‎ A．七 B．一 C．十 D．中 考点： 专题：正方体相对两个面上的文字．‎ 分析： 正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．‎ 解答： 解：正方体的表面展开图，相对的面之间一定相隔一个正方形，‎ ‎“我”与“十”是相对面，‎ ‎“爱”与“一”是相对面，‎ ‎“七”与“中”是相对面．‎ 故选B．‎ 点评： 本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．‎ ‎　‎ ‎3．下列说法不正确的是（　　）‎ A．0既不是正数，也不是负数 B．互为相反数的两个数的和为0‎ C．互为倒数的两个数的和为1‎ D．0的绝对值是0‎ 考点： 倒数；正数和负数；相反数；绝对值．‎ 分析： 根据零的意义，可判断A，根据相反数的关系，可判断B，根据倒数的定义，可判断C，根据绝对值的意义，可判断D．‎ 解答： 解：A、0既不是正数也不是负数，故A正确；‎ B、互为相反数的和为零，故B正确；‎ C、互为倒数的两个数的积为1，故C错误；‎ D、0的绝对值是0，故D正确；‎ 故选：C．‎ 点评： 本题考查了倒数，乘积为1的两个数互为倒数．‎ ‎　‎ ‎4．A为数轴上表示2的点，将点A沿数轴向左平移7个单位到点B，再由B向右平移6个单位到点C，则点C所表示的数是（　　）‎ A．11 B．1 C．2 D．3‎ 考点： 数轴．‎ 分析： 根据数轴规定向右为正方向，则向右平移，用加；向左平移，用减求解．‎ 解答： 解：B的点表示的数为2﹣7=﹣5，点C所表示的数是﹣5+6=1．‎ 故选：B．‎ 点评： 本题主要考查了数轴，解题的关键是数轴上的数移运时用左减右加．‎ ‎　‎ ‎5．在﹣，﹣|12|，﹣20，0，﹣（﹣5）中，负数的个数有（　　）‎ A．2个 B．3 个 C．4 个 D．5 个 考点： 正数和负数．‎ 分析： 根据绝对值、相反数，可化简数，根据小于零的数是负数，可得答案．‎ 解答： 解：﹣＜0，﹣|12|=﹣12＜0，﹣20＜0，0=0，﹣（﹣5）=5＞0，‎ ‎∴﹣，﹣|12|，﹣20是负数，‎ 故选：B．‎ 点评： 本题考查了正数和负数，判断一个数是正数还是负数，要把它化简成最后形式再判断．概念：用正数表示其中一种意义的量，另一种量用负数表示；特别地，在用正负数表示向指定方向变化的量时，通常把向指定方向变化的量规定为正数，而把向指定方向的相反方向变化的量规定为负数．‎ ‎　‎ ‎6．如图所示，关于线段、射线和直线的条数，下列说法正确的是（　　）‎ A．五条线段，三条射线 B．一条直线，三条线段 C．三条线段，两条射线，一条直线 D．三条线段，三条射线 考点： 直线、射线、线段．‎ 分析： 利用直线，射线及线段的特征求解即可．‎ 解答： 解：由图形可得有三条线段，两条射线，一条直线．‎ 故选：C．‎ 点评： 本题主要考查了直线，射线及线段，解题的关键是熟记直线，射线及线段的特征．‎ ‎　‎ ‎7．一种上衣每件成本为60元，按高出成本价的25%标价出售，后因库存积压，又按标价的80%出售，每件上衣还能盈利（　　）‎ A．0元 B．1.5元 C．4.8元 D．5元 考点： 有理数的混合运算．‎ 专题： 应用题．‎ 分析： 根据题意列出算式，计算即可得到结果．‎ 解答： 解：根据题意得：60×（1+25%）×80%﹣60=0（元），‎ 则每件上衣还能盈利0元．‎ 故选A 点评： 此题考查了有理数的混合运算，弄清题意是解本题的关键．‎ ‎　‎ ‎8．去括号正确的是（　　）‎ A．﹣（a+b﹣c）=﹣a+b﹣c B．﹣2（a+b﹣3c）=﹣2a﹣2b+6c C．3a﹣2b﹣（﹣a﹣b﹣c）=﹣a+ba+c D．﹣（a﹣b﹣c）=﹣a+b﹣c 考点： 去括号与添括号．‎ 分析： 直接利用去括号法则进而判断得出即可．‎ 解答： 解：A、﹣（a+b﹣c）=﹣a﹣b+c，故此选项错误；‎ B、﹣2（a+b﹣3c）=﹣2a﹣2b+6c，正确；‎ C、3a﹣2b﹣（﹣a﹣b﹣c）=4a﹣b+c，故此选项错误；‎ D、﹣（a﹣b﹣c）=﹣a+b+c，故此选项错误；‎ 故选：B．‎ 点评： 此题主要考查了去括号法则的应用，正确去括号是解题关键．‎ ‎　‎ ‎9．下列说法中，正确的是（　　）‎ A．若|a|=a，则a=0‎ B．两点之间，直线最短 C．直线AB和直线BA是同一条直线 D．多项式x3+x2的次数是5‎ 考点： 绝对值；多项式；直线、射线、线段；线段的性质：两点之间线段最短．‎ 专题： 计算题．‎ 分析： 利用绝对值的代数意义，多项式的次数，以及直线的定义，线段的性质判断即可．‎ 解答： 解：A、若|a|=a，则a为非负数，错误；‎ B、两点之间，线段最短，错误；‎ C、直线AB与直线BA是同一条直线，正确；‎ D、多项式x3+x2的次数是3，错误，‎ 故选C 点评：此题考查了绝对值，多项式，直线、射线、线段，以及线段的性质，熟练掌握各自的定义是解本题的关键．‎ ‎　‎ ‎10．如图，将一副三角尺按不同位置摆放，摆放方式中∠α与∠β互余的是（　　）‎ A． B． C． D．‎ 考点： 余角和补角．‎ 分析： 根据图形，结合互余的定义判断即可．‎ 解答： 解：A、∠α与∠β不互余，故本选项错误；‎ B、∠α与∠β不互余，故本选项错误；‎ C、∠α与∠β互余，故本选项正确；‎ D、∠α与∠β不互余，∠α和∠β互补，故本选项错误；‎ 故选C．‎ 点评： 本题考查了对余角和补角的应用，主要考查学生的观察图形的能力和理解能力．‎ ‎　‎ ‎11．如图①是一块瓷砖的图案，用这种瓷砖来铺设地面，如果铺成一个2×2的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个3×3的正方形图案（如图③），其中完整的圆共有13个，如果铺成一个4×4的正方形图案（如图④），其中完整的圆共有25个，若这样铺成一个10×10的正方形图案，则其中完整的圆共有（　　）个．‎ A．145 B．146 C．180 D．181‎ 考点： 规律型：图形的变化类．‎ 分析： 根据给出的四个图形的规律可以知道，组成大正方形的每个小正方形上有一个完整的圆，因此圆的数目是大正方形边长的平方，每四个小正方形组成一个完整的圆，从而可得这样的圆是大正方形边长减1的平方，从而可得若这样铺成一个10×10的正方形图案，则其中完整的圆共有102+（10﹣1）2=181个．‎ 解答： 解：分析可得完整的圆是大正方形的边长减1的平方，从而可知铺成一个10×10的正方形图案中，完整的圆共有102+（10﹣1）2=181个．‎ 故选D．‎ 点评： 本题难度中等，考查探究图形的规律．本题也只可以直接根据给出的四个图形中计数出的圆的个数，找出数字之间的规律得出答案．‎ ‎　‎ ‎12．已知a、b、c在数轴上的位置如图所示，化简|b﹣a|+|2a+c|﹣|c﹣b|的结果是（　　）‎ A．﹣a﹣2c B．3a C．a D．3a﹣2b 考点： 整式的加减；数轴；绝对值．菁优网版权所有 专题： 计算题．‎ 分析： 根据数轴上点的位置判断出绝对值里边式子的正负，利用绝对值的代数意义化简，计算即可得到结果．‎ 解答： 解：根据数轴上点的位置得：b＜c＜0＜a，‎ ‎∴b﹣a＜0，2a+c＞0，c﹣b＞0，‎ 则原式=a﹣b+2a+c﹣c+b=3a，‎ 故选：B．‎ 点评： 此题考查了整式的加减，数轴以及绝对值，熟练掌握运算法则是解本题的关键．‎ ‎　‎ 二、填空题：（本大题6个小题，每小题4分，共24分）在每小题中，请将答案直接填在答题卷中对应的横线上．‎ ‎13．2014年12月8日“全国目标教学展示”在71中举行．来自全国的选手共展示了47节课，参加听课的师生共有2748人次，请将2748用科学记数法表示为　2.748×103　．‎ 考点： 科学记数法—表示较大的数．‎ 分析： 科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．‎ 解答： 解：2748=2.748×103；‎ 故答案为：2.748×103．‎ 点评： 此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．‎ ‎　‎ ‎14．单项式﹣πa2bc的系数是　﹣π　；次数是　4　．‎ 考点： 单项式．‎ 分析： 根据单项式系数及次数的定义，即可得出答案．‎ 解答： 解：单项式﹣πa2bc的系数是﹣π；次数是4．‎ 故答案为：﹣π，4．‎ 点评： 本题考查了单项式的知识，解答本题的关键是掌握单项式系数及次数的定义．‎ ‎　‎ ‎15．∠A=32°36′，它的补角为　147°24′　．‎ 考点： 余角和补角；度分秒的换算．‎ 分析： 根据两个角的和等于180°，则这两个角互补，可得答案．‎ 解答： 解：由补角的定义，得 ‎∠A的补角=180°﹣∠A=180°﹣32°36′=147°24′，‎ 故答案为：147°24′．‎ 点评： 本题考查了余角和补角，利用了补角的定义．‎ ‎　‎ ‎16．多项式5x2y+y3﹣3xy2﹣x3按x的降幂排列是　﹣x3+5x2y﹣3xy2+y3　．‎ 考点： 多项式．‎ 分析： 按x的指数从大到小排列即可．‎ 解答： 解：多项式5x2y+y3﹣3xy2﹣x3按x的降幂排列是﹣x3+5x2y﹣3xy2+y3．‎ 点评： 考查的知识点为：把一个多项式的各项按照某个字母的指数从大到小或从小到大的顺序排列，称为按这个字母的降幂或升幂排列．要注意，在排列多项式各项时，要保持其原有的符号．‎ ‎　‎ ‎17．已知代数式2a3bn+1与﹣3am﹣2b2是同类项，则2m+3n=　13　．‎ 考点： 同类项．‎ 分析： 本题考查同类项的定义（所含字母相同，相同字母的指数相同），可得：m﹣2=3，n+1=2，解方程即可求得m，n的值，从而求出2m+3n的值．‎ 解答：解：由同类项的定义，‎ 可知m﹣2=3，n+1=2，‎ 解得n=1，m=5，‎ 则2m+3n=13．‎ 故答案为：13‎ 点评： 同类项定义中的两个“相同”：所含字母相同，相同字母的指数相同，是易混点，因此成了中考的常考点．‎ ‎　‎ ‎18．观察下面一列有规律的数，根据这个规律可知第n个数是　　（n是正整数）‎ 考点： 规律型：数字的变化类．‎ 分析： 观察这列数发现，每一个数都是分数，其中分子等于序号，分母是分子加1的平方减去1，由此即可求解．‎ 解答： 解：∵第1个数是：=，‎ 第2个数是：=，‎ 第3个数是：=，‎ 第4个数是：=，‎ ‎…‎ ‎∴第n个数是．‎ 故答案为：．‎ 点评： 考查了规律型：数字的变化．本题是一道找规律的题目，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．找分数的规律时，一定要分别观察分数的分子和分母的规律．‎ ‎　‎ 三、解答题：（本大题2个小题，每小题7分，共14分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答书写在答题卷中对应的位置上．‎ ‎19．计算：‎ ‎（1）﹣7+13﹣6+20； ‎ ‎（2）．‎ 考点： 有理数的混合运算．‎ 专题： 计算题．‎ 分析： （1）原式结合后，相加即可得到结果；‎ ‎（2）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果．‎ 解答： 解：（1）原式=﹣13+13+20=20；‎ ‎（2）原式=9×（﹣）+8÷4=﹣3+2=﹣1．‎ 点评： 此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．‎ ‎　‎ ‎20．作图题．如图，在同一平面内有四个点A、B、C、D，‎ ‎①画射线BD； ‎ ‎②画直线BC； ‎ ‎③连结AC与射线BD相交于点P；‎ ‎④延长线段AD与直线BC相交于点Q．‎ 考点： 直线、射线、线段．‎ 专题： 作图题．‎ 分析： 根据直线：向两方无限延伸；射线向一方无限延伸；线段：本身不能向两方无限延伸，画出图形即可．‎ 解答： 解：如图所示：‎ ‎．‎ 点评： 此题主要考查了直线、射线、线段，关键是掌握三种线的特点．‎ ‎　‎ 四、解答题（每题10分，共40分）‎ ‎21．计算：‎ ‎（1）2（x2y+xy2）﹣3（x2y﹣5x）﹣2xy2﹣7x；‎ ‎（2）．‎ 考点： 有理数的混合运算；整式的加减．‎ 专题： 计算题．‎ 分析： （1）原式去括号合并即可得到结果；‎ ‎（2）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果．‎ 解答： 解：（1）原式=2x2y+2xy2﹣3x2y+15x﹣2xy2﹣7x=﹣x2y+8x；‎ ‎（2）原式=4+4×+×（﹣16）=4+6﹣1=9．‎ 点评： 此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．‎ ‎　‎ ‎22．先化简，再求值：‎ 已知：（a+1）2+|b+2|=0，求代数式﹣a2b+（3ab2﹣a2b）﹣2（2ab2﹣a2b）的值．‎ 考点： 整式的加减—化简求值；非负数的性质：绝对值；非负数的性质：偶次方．‎ 专题： 计算题．‎ 分析： 原式去括号合并得到最简结果，利用非负数的性质求出a与b的值，代入原式计算即可．‎ 解答： 解：∵（a+1）2≥0，|b+2|≥0，且（a+1）2+|b+2|=0，‎ ‎∴a=﹣1，b=﹣2，‎ ‎∵﹣a2b+（3ab2﹣a2b）﹣2（2ab2﹣a2b）‎ ‎=﹣a2b+3ab2﹣a2b﹣4ab2+2a2b ‎=﹣ab2，‎ 把 a=﹣1，b=﹣2代入代数式得：﹣ab2=﹣（﹣1）×（﹣2）2=4．‎ 点评： 此题考查了整式的加减﹣化简求值，以及非负数的性质，熟练掌握运算法则是解本题的关键．‎ ‎　‎ ‎23．如图，OE为∠AOD的平分线，∠COD=∠EOC，∠COD=15°，‎ 求：①∠EOC的大小； ②∠AOD的大小．‎ 考点： 角平分线的定义．‎ 分析： ①根据∠COD=∠EOC，可得∠EOC=4∠COD；‎ ‎②根据角的和差，可得∠EOD的大小，根据角平分线的性质，可得答案．‎ 解答： 解：①由∠COD=∠EOC，得 ‎∠EOC=4∠COD=4×15°=60°；‎ ‎②由角的和差，得 ‎∠EOD=∠EOC﹣∠COD=60°﹣15°=45°．‎ 由角平分线的性质，得 ‎∠AOD=2∠EOD=2×45°=90°．‎ 点评： 本题考查了角平分线的定义，利用了角平分线的性质，角的和差．‎ ‎　‎ ‎24．如图已知点C为AB上一点，AC=12cm，CB=AC，D、E分别为AC、AB的中点，求DE的长．‎ 考点： 比较线段的长短．‎ 分析： 求DE的长度，即求出AD和AE的长度．因为D、E分别为AC、AB的中点，故DE=，又AC=12cm，CB=AC，可求出CB，即可求出CB，代入上述代数式，即可求出DE的长度．‎ 解答： 解：根据题意，AC=12cm，CB=AC，‎ 所以CB=8cm，‎ 所以AB=AC+CB=20cm，‎ 又D、E分别为AC、AB的中点，‎ 所以DE=AE﹣AD=（AB﹣AC）=4cm．‎ 即DE=4cm．‎ 故答案为4cm．‎ 点评： 此题要求学生灵活运用线段的和、差、倍、分之间的数量关系，熟练掌握．‎ ‎　‎ 四、解答题：（每小题12分，共24分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答书写在答题卷中对应的位置上 ‎25．重庆某餐饮集团公司将沙坪坝下属一个分公司对外招商承包，有符合条件的两个企业甲、乙，分别拟定上缴利润方案如下：‎ 甲：每年结算一次上缴利润，第一年上缴利润5万元，以后每年比前一年增加5万元；‎ 乙：每半年结算一次上缴利润，第一个半年上缴利润1.5万元，以后每半年比前一半年增加1.5万元；‎ ‎（1）如果企业乙承包一年，则需上缴的总利润为　4.5　万元．‎ ‎（2）如果承包4年，你认为应该承包给哪家企业，总公司获利多？为什么？‎ ‎（3）如果承包n年，请你用含n的代数式分别表示两企业上缴利润的总金额（单位：万元）．‎ 考点： 列代数式；有理数的混合运算．‎ 分析： （1）企业乙承包一年：上半年上缴利润1.5万元，下半年上缴利润（1.5+1.5）万元；‎ ‎（2）根据两企业的利润方案计算即可；‎ ‎（3）归纳总结，根据题意列出两企业上缴利润的总金额即可．‎ 解答： 解：（1）1.5+（1.5+1.5）=4.5（万元）．‎ 故答案是：4.5；‎ ‎（2）由题意，企业甲承包4年上缴的利润为：5+10+15+20=50（万元） ‎ 企业乙承包4年上缴的利润为：1.5+3+4.5+6+7.5+9+10.5+12=54（万元） ‎ ‎54﹣50=4（万元），胡企业乙比企业甲上缴利润多4万元，所以该承包给企业乙，总公司获利多．‎ ‎（3）根据题意得：‎ 企业甲承包n年上缴的利润总金额为5+10+15+20+…+5n=5×（1+2+3+…+n）=（万元）；‎ 企业乙承包n年上缴的利润总金额为1.5+1.5×2+1.5×3+…+1.5×2n=1.5×（1+2+3+…+2n）=1.5n（2n+1）（万元）．‎ 点评： 考查了列代数式及代数式求值的知识，解题的关键是仔细审题，难度不大．‎ ‎26．近年来，随着社会竞争的日益激烈，家长为使孩子不输在教育的起跑线上，不惜花费重金购置教育质量好的学区的房产．张先生准备购买一套小户型学区房，他去某楼盘了解情况得知，该户型的单价是12000元/m2，面积如图所示（单位：米，卫生间的宽未定，设宽为x米），售房部为张先生提供了以下两种优惠方案：‎ 方案一：整套房的单价是12000元/m2，其中厨房可免费赠送的面积；‎ 方案二：整套房按原销售总金额的9折出售．‎ ‎（1）用y1表示方案一中购买一套该户型商品房的总金额，用y2表示方案二中购买一套该户型商品房的总金额，分别求出两种方案中的总金额y1、y2（用含x的式子表示）；‎ ‎（2）求当x=2时，两种方案的总金额分别是多少元？‎ ‎（3）张先生因现金不够，在银行借了18万元住房贷款，贷款期限为6年，从开始贷款的下一个月起逐月偿还，贷款月利率是0.5%，每月还款数额=平均每月应还的贷款本金数额+月利息，月利息=上月所剩贷款本金数额×月利率．‎ ‎①张先生借款后第一个月应还款数额是多少元？‎ ‎②假设贷款月利率不变，若张先生在借款后第n（1≤n≤72，n是正整数）个月的还款数额为P，请写出P与n之间的关系式．‎ 考点： 列代数式；代数式求值．‎ 分析： （1）根据图中线段长度，即可表示出各部分面积，进而得出两种购买方案；‎ ‎（2）利用两关系式直接得出答案；‎ ‎（3）①根据贷款数以及利率即可得出张先生借款后第一个月应还款数额；‎ ‎②可以得出还款数额为2500+[180000﹣（n﹣1）×2500]×0.5%，进而得出即可．‎ 解答： 解：（1）y1=12000×（18+12+6×+2x）=12000×（2x+32）=24000x+384000，‎ ‎ y2=12000×（18+12+6+2x）×0.9=12000×（2x+36）×0.9=21600x+388800；‎ ‎（2）当x=2时，y1=2400×2+384000=432000（元）；‎ y2=21600×2+388800=432000（元）；‎ 故当x=2时，两种方案的金额均为432000元．‎ ‎（3）①180000÷（12×6）=2500（元）2500+180000×0.5%=3400（元）‎ 答：张先生借款后第一个月应还3400元． ‎ ‎②P=2500+[180000﹣2500（n﹣1）]×0.5%=﹣12.5n+3412.5．‎ 点评： 此题主要考查了一次函数的综合应用，根据已知正确利用每月还款数额=平均每月应还的贷款本金数额+月利息，月利息=上月所剩贷款本金数额×月利率这些公式是解题关键．‎