七年级上9月考试卷 17页

‎2014-2015学年重庆市110中学七年级（上）第一次月考数学试卷 ‎　‎ 一、选择题（共15小题，每小题3分，满分45分）‎ ‎1．﹣5的相反数是（　　）‎ A．5 B．﹣5 C． D．‎ ‎　‎ ‎2．计算：﹣2+3=（　　）‎ A．1 B．﹣1 C．﹣5 D．﹣6‎ ‎　‎ ‎3．数轴上表示﹣3的点与表示+5的点的距离是（　　）‎ A．3 B．﹣2 C．+2 D．8‎ ‎　‎ ‎4．如图，用一个平面去截圆锥，得到的截面是（　　）‎ A． B． C． D．‎ ‎　‎ ‎5．一袋大米的标准重量为10kg．把一袋重10.5kg的大米记为+0.5kg，则一袋重9.8kg的大米记为（　　）‎ A．﹣9.8kg B．+9.8kg C．﹣0.2kg D．0.2kg ‎　‎ ‎6．如图下面的图形中，是三棱柱的侧面展开图的为（　　）‎ A． B． C． D．‎ ‎　‎ ‎7．绝对值比2大的数是（　　）‎ A．﹣3 B．0 C．1 D．2‎ ‎　‎ ‎8．有理数+2，﹣1，，7，0中，不属于正数集合的是（　　）‎ A．﹣1 B．﹣1和 C．﹣1和0 D．和0‎ ‎　‎ ‎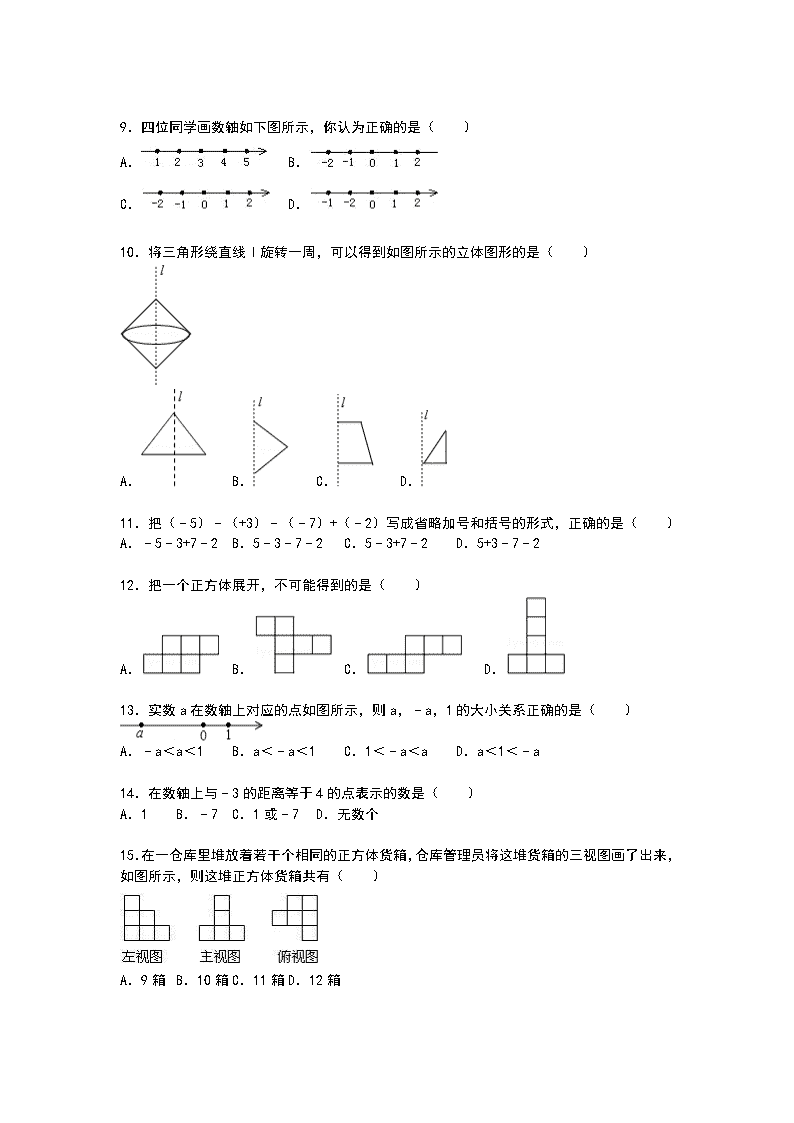9．四位同学画数轴如下图所示，你认为正确的是（　　）‎ A． B． ‎ C． D．‎ ‎　‎ ‎10．将三角形绕直线l旋转一周，可以得到如图所示的立体图形的是（　　）‎ A． B． C． D．‎ ‎　‎ ‎11．把（﹣5）﹣（+3）﹣（﹣7）+（﹣2）写成省略加号和括号的形式，正确的是（　　）‎ A．﹣5﹣3+7﹣2 B．5﹣3﹣7﹣2 C．5﹣3+7﹣2 D．5+3﹣7﹣2‎ ‎　‎ ‎12．把一个正方体展开，不可能得到的是（　　）‎ A． B． C． D．‎ ‎　‎ ‎13．实数a在数轴上对应的点如图所示，则a，﹣a，1的大小关系正确的是（　　）‎ A．﹣a＜a＜1 B．a＜﹣a＜1 C．1＜﹣a＜a D．a＜1＜﹣a ‎　‎ ‎14．在数轴上与﹣3的距离等于4的点表示的数是（　　）‎ A．1 B．﹣7 C．1或﹣7 D．无数个 ‎　‎ ‎15．在一仓库里堆放着若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画了出来，如图所示，则这堆正方体货箱共有（　　）‎ A．9箱 B．10箱 C．11箱 D．12箱 ‎　‎ ‎　‎ 二、耐心填一填：（每空2分，共36分）请将答案直接填写在题后的横线上 ‎16．A盆地海拔是﹣10m，B盆地海拔是﹣15m，那么　　　　　　的地势较高（填“A”或“B”）．‎ ‎　‎ ‎17．月球表面温度，中午是101℃，半夜是﹣150℃，则半夜比中午低　　　　　　℃．‎ ‎　‎ ‎18．计算：﹣3+4=　　　　　　，3﹣|﹣6|=　　　　　　，﹣2﹣1=　　　　　　，0﹣6=　　　　　　．‎ ‎　‎ ‎19．互为相反数两数和为　　　　　　．‎ ‎　‎ ‎20．当下面这个图案被折起来组成一个正方体，数字　　　　　　会在与数字2所在的平面相对的平面上．‎ ‎　‎ ‎21．﹣的绝对值是　　　　　　，相反数是　　　　　　，若|x|=3，则x=　　　　　　．‎ ‎　‎ ‎22．比较大小：（填“＞”或“＜”）‎ ‎（1）﹣24　　　　　　2； （2）﹣1.5　　　　　　0； （3）0　　　　　　|﹣8|；（4）﹣　　　　　　﹣．‎ ‎　‎ ‎23．在数轴上，老师不小心把一滴墨水滴在画好的数轴上，如图所示，试根据图中标出的数值判断被墨水盖住的整数　　　　　　．‎ ‎　‎ ‎24．观察下面一列数，探究其中的规律：﹣1，，﹣，，﹣， …第11个数是　　　　　　．‎ ‎　‎ ‎25．一个立方体的每个面上都标有数字1、2、3、4、5、6，根据图中该立方体A、B、C三种状态所显示的数字，可推出“？”处的数字是　　　　　　‎ ‎　‎ ‎　‎ 三、解答题（共2小题，满分14分）‎ ‎26．在数轴上表示下列各数，再把这些数用“＜”号连接起来．‎ ‎3，﹣1.5，﹣3，0，2.5，﹣4．‎ ‎　‎ ‎27．如图是由7个相同边长为1个单位的小正方体搭成的一个几何体，‎ ‎（1）画出它的三视图；‎ ‎（2）求出它的表面积．‎ ‎　‎ ‎　‎ 四、仔细填一填：（共8分）‎ ‎28．下列各数填入相应的大括号里：‎ ‎5，﹣1，0，﹣6，π，0.3，﹣3，+5，﹣0.72，…‎ ‎①正数集合：{ …} ②整数集合：{ …}‎ ‎③负数集合：{ …} ④分数集合：{ …}．‎ ‎　‎ ‎29．计算下列各题：‎ ‎（1）49+（﹣23）+（﹣35）+0‎ ‎（2）19﹣（﹣76）﹣22﹣（﹣52）‎ ‎（3）（﹣6）﹣（﹣）+（﹣4）﹣‎ ‎（4）0.5+（﹣）﹣（﹣3.75）+‎ ‎（5）（﹣）﹣7﹣（﹣3.2）+（﹣1）‎ ‎（6）﹣1.6+3.2﹣0.4﹣3+1.8．‎ ‎　‎ ‎30．一辆汽车沿着一条南北方向的公路来回行驶．某一天早晨从A地出发，晚上到达B地．约定向北为 正，向南为负，当天记录如下：（单位：千米）﹣18.3，﹣9.5，+7.1，﹣14，﹣6.2，+13，﹣6.8，﹣8.5‎ ‎（1）问B地在A地何处，相距多少千米？（2）若汽车行驶每千米耗油0.2升，那么这一天共耗油多少升？‎ ‎　‎ ‎31．从2开始，连续偶数相加，它们和的情况如下表：‎ 加数的个数 和 ‎1 2=1×2‎ ‎2 2+4=6=2×3‎ ‎3 2+4+6=12=3×4‎ ‎4 2+4+6+8=20=4×5‎ ‎… …‎ 观察上面的式子有怎样的规律，并用你发现的规律来计算：‎ ‎（1）2+4+6+8+…+202‎ ‎（2）126+128+130+…+300．‎ ‎　‎ ‎　‎ ‎2014-2015学年重庆市110中学七年级（上）第一次月考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（共15小题，每小题3分，满分45分）‎ ‎1．﹣5的相反数是（　　）‎ A．5 B．﹣5 C． D．‎ 考点： 相反数．‎ 分析： 根据只有符号不同的两个数互为相反数，可得一个数的相反数．‎ 解答： 解：﹣5的相反数是5，‎ 故选：A．‎ 点评： 本题考查了相反数，在一个数的前面加上负号就是这个数的相反数．‎ ‎　‎ ‎2．计算：﹣2+3=（　　）‎ A．1 B．﹣1 C．﹣5 D．﹣6‎ 考点： 有理数的加法．‎ 分析： 根据绝对值不等的异号加减，取绝对值较大的加数符号，并用较大的绝对值减去较小的绝对值计算即可．‎ 解答： 解：﹣2+3=1．‎ 故选A．‎ 点评： 此题主要考查了有理数的加法运算，在进行有理数加法运算时，首先判断两个加数的符号：是同号还是异号，是否有0，从而确定用哪一条法则．‎ ‎　‎ ‎3．数轴上表示﹣3的点与表示+5的点的距离是（　　）‎ A．3 B．﹣2 C．+2 D．8‎ 考点： 数轴；有理数的减法．‎ 分析： 数轴上两点间的距离的求法：数轴上两点间的距离即数轴上表示两个点的数的差的绝对值．‎ 解答： 解：∵5﹣（﹣3）=8，‎ ‎∴数轴上表示﹣3的点与表示+5的点的距离是8．‎ 故选D．‎ 点评： 考查了数轴上两点间的距离计算方法，熟练进行有理数的减法运算．‎ ‎　‎ ‎4．如图，用一个平面去截圆锥，得到的截面是（　　）‎ A． B． C． D．‎ 考点： 截一个几何体．‎ 分析： 由图可知，平面经过顶点和底面，那么截得的图形应该是个等腰三角形．‎ 解答： 解：由图可知，平面经过顶点和底面，那么截得的图形应该是个等腰三角形，故选A．‎ 点评： 截面的形状既与被截的几何体有关，还与截面的角度和方向有关．对于这类题，最好是动手动脑相结合，亲自动手做一做，从中学会分析和归纳的思想方法．‎ ‎　‎ ‎5．一袋大米的标准重量为10kg．把一袋重10.5kg的大米记为+0.5kg，则一袋重9.8kg的大米记为（　　）‎ A．﹣9.8kg B．+9.8kg C．﹣0.2kg D．0.2kg 考点： 正数和负数．‎ 分析： 根据正、负数的意义列式计算即可得解．‎ 解答： 解：∵多于标准重量0.5kg的面粉记作+0.5kg，‎ ‎∴低于标准重量0.2kg的面粉记作﹣0.2kg．‎ 故选C．‎ 点评： 此题主要考查了正负数的意义，解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．‎ ‎　‎ ‎6．如图下面的图形中，是三棱柱的侧面展开图的为（　　）‎ A． B． C． D．‎ 考点： 几何体的展开图．‎ 分析： 利用三棱柱及其表面展开图的特点解题．注意三棱柱的侧面展开图是三个小长方形组合成的大长方形．‎ 解答： 解：三棱柱的侧面展开图是一个三个小长方形组合成的矩形．‎ 故选A．‎ 点评： 本题考查了三棱柱的侧面展开图，三棱柱的侧面展开图是长方形．‎ ‎　‎ ‎7．绝对值比2大的数是（　　）‎ A．﹣3 B．0 C．1 D．2‎ 考点： 绝对值．‎ 分析： 计算绝对值要根据绝对值的定义求解．第一步列出绝对值的表达式；第二步根据绝对值定义去掉这个绝对值的符号．‎ 解答： 解：|﹣3|=3＞2；|0|=0＜2；|1|=1＜2；|2|=2．‎ 故选A．‎ 点评： 考查了绝对值的知识，规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．‎ ‎　‎ ‎8．有理数+2，﹣1，，7，0中，不属于正数集合的是（　　）‎ A．﹣1 B．﹣1和 C．﹣1和0 D．和0‎ 考点： 正数和负数．‎ 专题： 常规题型．‎ 分析： 根据正数和负数的定义即可作出判断．‎ 解答： 解：有理数+2，﹣1，，7，0中，‎ 负数有：﹣1；‎ 正数有：+2，5，7．‎ ‎0既不是正数，也不是负数．‎ 故选C．‎ 点评： 本题考查了正数和负数的知识，属于基础题，难度不大，注意基础概念的熟练掌握．‎ ‎　‎ ‎9．四位同学画数轴如下图所示，你认为正确的是（　　）‎ A． B． ‎ C． D．‎ 考点： 数轴．‎ 分析： 数轴的定义：规定了原点、单位长度和正方向的直线．‎ 解答： 解：A中，无原点；‎ B中，无正方向；‎ D中，数的顺序错了．‎ 故选C．‎ 点评： 考查了数轴的定义．‎ 注意数轴的三要素：原点、正方向和单位长度．‎ ‎　‎ ‎10．将三角形绕直线l旋转一周，可以得到如图所示的立体图形的是（　　）‎ A． B． C． D．‎ 考点： 点、线、面、体．‎ 分析：将各选项的图形旋转即可得到立体图形，找到合适的即可．‎ 解答： 解：A、旋转后可得，故本选项错误；‎ B、旋转后可得，故本选项正确；‎ C、旋转后可得，故本选项错误；‎ D、旋转后可得，故本选项错误．‎ 故选B．‎ 点评： 本题考查学生立体图形的空间想象能力及分析问题，解决问题的能力，画出正确图形即可解答．‎ ‎　‎ ‎11．把（﹣5）﹣（+3）﹣（﹣7）+（﹣2）写成省略加号和括号的形式，正确的是（　　）‎ A．﹣5﹣3+7﹣2 B．5﹣3﹣7﹣2 C．5﹣3+7﹣2 D．5+3﹣7﹣2‎ 考点： 有理数的加减混合运算．‎ 专题： 计算题．‎ 分析： 原式去括号即可得到结果．‎ 解答： 解：原式=﹣5﹣3+7﹣2，‎ 故选A 点评： 此题考查了有理数的加减混合运算，熟练掌握运算法则是解本题的关键．‎ ‎　‎ ‎12．把一个正方体展开，不可能得到的是（　　）‎ A． B． C． D．‎ 考点： 几何体的展开图．‎ 分析： 根据平面图形的折叠及正方体的展开图解题．‎ 解答： 解：B、C、D都是正方体的展开图，故选项A错误；‎ 故选：A．‎ 点评： 本题考查了正方体的展开图，解题的关键是熟记正方体展开图的各种情形．‎ ‎　‎ ‎13．实数a在数轴上对应的点如图所示，则a，﹣a，1的大小关系正确的是（　　）‎ A．﹣a＜a＜1 B．a＜﹣a＜1 C．1＜﹣a＜a D．a＜1＜﹣a 考点： 实数与数轴；实数大小比较．‎ 专题： 压轴题．‎ 分析： 本题首先运用数形结合的思想确定a的正负情况，然后根据相反数意义即可解题．‎ 解答： 解：由数轴上a的位置可知a＜0，|a|＞1；‎ 设a=﹣2，则﹣a=2，‎ ‎∵﹣2＜1＜2‎ ‎∴a＜1＜﹣a，‎ 故选项A，B，C错误，选项D正确．‎ 故选D．‎ 点评： 此题主要考查了比较实数的大小，解答此题的关键是根据数轴上a的位置估算出a的值，设出符合条件的数值，再比较大小即可．‎ ‎　‎ ‎14．在数轴上与﹣3的距离等于4的点表示的数是（　　）‎ A．1 B．﹣7 C．1或﹣7 D．无数个 考点： 数轴．‎ 分析： 此题注意考虑两种情况：该点在﹣3的左侧，该点在﹣3的右侧．‎ 解答： 解：根据数轴的意义可知，在数轴上与﹣3的距离等于4的点表示的数是﹣3+4=1或﹣3﹣4=﹣7．‎ 故选C．‎ 点评： 主要考查了数轴，要注意数轴上距离某个点是一个定值的点有两个，左右各一个，不要漏掉一种情况．把数和点对应起来，也就是把“数”和“形”结合起来，二者互相补充，相辅相成，把很多复杂的问题转化为简单的问题，在学习中要注意培养数形结合的数学思想．‎ ‎　‎ ‎15．在一仓库里堆放着若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画了出来，如图所示，则这堆正方体货箱共有（　　）‎ A．9箱 B．10箱 C．11箱 D．12箱 考点： 由三视图判断几何体．‎ 专题： 压轴题．‎ 分析： 根据三视图可得出，货箱的底层共有3+2+1个箱子，第二层有2层，第三层有1箱．‎ 解答： 解：综合三视图可以得出，这堆货箱的底层有3+2+1=6箱，第二层有2箱，第三层应该有1箱，‎ 因此这堆正方体货箱共有6+2+1=9箱．故选A．‎ 点评：本题意在考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就更容易得到答案．‎ ‎　‎ 二、耐心填一填：（每空2分，共36分）请将答案直接填写在题后的横线上 ‎16．A盆地海拔是﹣10m，B盆地海拔是﹣15m，那么　A　的地势较高（填“A”或“B”）．‎ 考点： 有理数大小比较．‎ 专题： 应用题．‎ 分析： 同为负数的两个数，绝对值大的比较小，绝对值小的比较大．所以，A盆地的地势比B盆地的地势高．‎ 解答： 解：A盆地海拔是﹣10m，即低于海平面10米；B盆地海拔是﹣15m，即低于海平面15米，故A盆地的地势较高．‎ 点评： 考查了同为负数的两个数，绝对值大的比较小，绝对值小的比较大．‎ ‎　‎ ‎17．月球表面温度，中午是101℃，半夜是﹣150℃，则半夜比中午低　251　℃．‎ 考点： 有理数的减法．‎ 分析： 用中午的温度减去半夜的温度，然后根据有理数的减法运算法则，减去一个数等于加上这个数的相反数计算即可得解．‎ 解答： 解：101﹣（﹣150），‎ ‎=101+150，‎ ‎=251℃．‎ 故答案为：251．‎ 点评： 本题考查了有理数的减法，熟记减去一个数等于加上这个数的相反数是解题的关键．‎ ‎　‎ ‎18．计算：﹣3+4=　1　，3﹣|﹣6|=　﹣3　，﹣2﹣1=　﹣3　，0﹣6=　﹣6　．‎ 考点： 有理数的减法；有理数的加法．‎ 分析： 根据有理数的减法法则：减去一个数，等于加上这个数的相反数进行计算即可．‎ 解答： 解：﹣3+4=1，‎ ‎3﹣|﹣6|=3﹣6=﹣3，‎ ‎﹣2﹣1=﹣2+（﹣1）=﹣3，‎ ‎0﹣6=0+（﹣6）=﹣6，‎ 故答案为：1；﹣3；﹣3；﹣6．‎ 点评： 此题主要考查了有理数的减法，关键是掌握有理数的减法法则．‎ ‎　‎ ‎19．互为相反数两数和为　0　．‎ 考点： 相反数．‎ 专题： 常规题型．‎ 分析： 根据互为相反数的两个数的和等于0解答．‎ 解答： 解：互为相反数两数和为0．‎ 故答案为：0．‎ 点评： 本题主要考查了互为相反数的定义，是概念题，熟记概念是解题的关键．‎ ‎　‎ ‎20．当下面这个图案被折起来组成一个正方体，数字　5　会在与数字2所在的平面相对的平面上．‎ 考点： 专题：正方体相对两个面上的文字．‎ 分析： 正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．‎ 解答： 解：正方体的表面展开图，相对的面之间一定相隔一个正方形，‎ 数字1与数字3是相对面，‎ 数字2与数字5是相对面，‎ 数字4与数字6是相对面．‎ 故答案为：5．‎ 点评： 本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．‎ ‎　‎ ‎21．﹣的绝对值是　　，相反数是　　，若|x|=3，则x=　+3和﹣3　．‎ 考点：绝对值；相反数．‎ 分析： 根据负数的绝对值等于﹣的相反数求出即可；根据相反数的定义求出﹣ 的相反数即可；根据绝对值为正数的数有两个，它们互为相反数直接写出答案即可．‎ 解答： 解：﹣的绝对值是，相反数是，若|x|=3，则x=3或﹣3，‎ 故答案为：，，3或﹣3．‎ 点评： 本题考查了对相反数，绝对值，有理数的平方等知识点的理解和运用，考查学生能否根据相反数、绝对值的意义求出任何数的相反数和绝对值．‎ ‎　‎ ‎22．比较大小：（填“＞”或“＜”）‎ ‎（1）﹣24　＜　2； （2）﹣1.5　＜　0； （3）0　＜　|﹣8|；（4）﹣　＞　﹣．‎ 考点： 有理数大小比较．‎ 分析： （1）根据正数大于负数，可得答案；‎ ‎（2）根据0大于负数，可得答案；‎ ‎（3）根据正数大于零，可得答案；‎ ‎（4）根据两个负数比较大小，绝对值大的数反而小，可得答案．‎ 解答： 解：（1）由正数大于负数，得﹣24＜2；‎ ‎（2）由0大于负数，得﹣1.5＜0；‎ ‎（3）由正数大于零，得0＜|﹣8|；‎ ‎（4）先求绝对值|﹣|=，|﹣|=，‎ ‎＜，即|﹣|＜|﹣|，‎ ‎﹣＞﹣，‎ 故答案为：＜，＜，＜，＞．‎ 点评： 本题考查了有理数大小比较，两个负数大小比较，绝对值大的数反而小．‎ ‎　‎ ‎23．在数轴上，老师不小心把一滴墨水滴在画好的数轴上，如图所示，试根据图中标出的数值判断被墨水盖住的整数　﹣12、﹣11、﹣10、﹣9、﹣8、11、12、13、14、15、16、17　．‎ 考点： 数轴．‎ 分析： 根据数轴上的点是连续的特点，写出被被墨水盖住的整数即可．‎ 解答： 解：根据数轴的特点，﹣12.6到﹣7.5之间的整数有﹣12、﹣11、﹣10、﹣9、﹣8，‎ ‎10.5到17.4之间的整数有11、12、13、14、15、16、17，‎ 所以，被墨水盖住的整数有﹣12、﹣11、﹣10、﹣9、﹣8、11、12、13、14、15、16、17．‎ 故答案为：﹣12、﹣11、﹣10、﹣9、﹣8、11、12、13、14、15、16、17．‎ 点评： 本题考查了数轴，是基础题，知道数轴上的点是连续的是解题的关键．‎ ‎　‎ ‎24．（2分）（2014秋•南岸区校级月考）观察下面一列数，探究其中的规律：﹣1，，﹣，，﹣， …第11个数是　﹣　．‎ 考点： 规律型：数字的变化类．‎ 分析： 分子都是1，分母是连续的自然数，奇数位置为负，偶数位置为正，由此写出答案即可．‎ 解答： 解：第11个数分别是﹣．‎ 故答案为：﹣．‎ 点评： 此题考查数字的变化规律，找出数字之间的联系，得出规律解决问题．‎ ‎　‎ ‎25．一个立方体的每个面上都标有数字1、2、3、4、5、6，根据图中该立方体A、B、C三种状态所显示的数字，可推出“？”处的数字是　6　‎ 考点： 专题：正方体相对两个面上的文字．‎ 分析： 通过观察可知1周围四个面分别是4，5，2，3，则1的对面是6；又与3相邻的数是1，2，5，6，则3的对面是4，则2与5相对，所以？定是1，6两个数中的一个，由于6同时和3、5相邻，则？处的数是6．‎ 解答： 解：由观察可知，‎ ‎1周围四个面分别是4，5，2，3，‎ 则1的对面是6；‎ 又与3相邻的数是1，2，5，6，‎ 则3的对面是4，则2与5相对，‎ 所以？一定是1，6两个数中的一个，‎ 又6同时和3、5相邻，则？处的数是6．‎ 故答案为：6．‎ 点评： 本题考查了正方体相对两个面上的文字，通过三个正方体中能看到的数字推出三组相对的数字是完成本题的关键．‎ ‎　‎ 三、解答题（共2小题，满分14分）‎ ‎26．在数轴上表示下列各数，再把这些数用“＜”号连接起来．‎ ‎3，﹣1.5，﹣3，0，2.5，﹣4．‎ 考点： 有理数大小比较；数轴．‎ 分析： 根据数轴是表示数的一条直线，可把数在数轴上表示出来，根据数轴上的点表示的数右边的总比左边的大，可得答案．‎ 解答： 解；如图，‎ 由数轴上的点表示的数右边的总比左边的大，得 ‎﹣4＜﹣3＜﹣1.5＜0＜2.5＜3．‎ 点评： 本题考查了有理数大小比较，利用了数轴比较有理数的大小．‎ ‎　‎ ‎27．如图是由7个相同边长为1个单位的小正方体搭成的一个几何体，‎ ‎（1）画出它的三视图；‎ ‎（2）求出它的表面积．‎ 考点： 作图-三视图；几何体的表面积．‎ 分析： （1）利用几何体的形状分别得出三视图即可；‎ ‎（2）利用几何体的形状得出小正方形的个数进而得出表面积．‎ 解答： 解：（1）如图所示：‎ ‎；‎ ‎（2）表面积为：（4+4+5+10+5）×1=28．‎ 点评： 此题主要考查了作三视图以及求几何体的表面积，利用几何体的形状得出视图是解题关键．‎ ‎　‎ 四、仔细填一填：（共8分）‎ ‎28．下列各数填入相应的大括号里：‎ ‎5，﹣1，0，﹣6，π，0.3，﹣3，+5，﹣0.72，…‎ ‎①正数集合：{ …} ②整数集合：{ …}‎ ‎③负数集合：{ …} ④分数集合：{ …}．‎ 考点： 有理数．‎ 分析： 根据整数，正数，负数，分数的意义选出后填上即可．‎ 解答： 解：①正数集合：{5，π，0.3，+5，…}；‎ ‎②整数集合：{5，﹣1，0，﹣6，…}；‎ ‎③负数集合：{﹣1，﹣6，﹣3，﹣0.72，…}；‎ ‎④分数集合：{0.3，﹣3，+5，﹣0.72，…}．‎ 点评： 本题考查了对有理数的有关概念的应用，注意：有理数包括整数和分数，整数包括正整数、0、负整数，分数包括正分数和负分数．‎ ‎　‎ ‎29．计算下列各题：‎ ‎（1）49+（﹣23）+（﹣35）+0 ‎ ‎（2）19﹣（﹣76）﹣22﹣（﹣52）‎ ‎（3）（﹣6）﹣（﹣）+（﹣4）﹣‎ ‎（4）0.5+（﹣）﹣（﹣3.75）+‎ ‎（5）（﹣）﹣7﹣（﹣3.2）+（﹣1）‎ ‎（6）﹣1.6+3.2﹣0.4﹣3+1.8．‎ 考点： 有理数的加减混合运算．‎ 专题： 计算题．‎ 分析： （1）原式结合后，相加即可得到结果；‎ ‎（2）原式利用减法法则变形，计算即可得到结果；‎ ‎（3）原式利用减法法则变形，计算即可得到结果；‎ ‎（4）原式利用减法法则变形，计算即可得到结果；‎ ‎（5）原式利用减法法则变形，计算即可得到结果；‎ ‎（6）原式结合后，相加即可得到结果．‎ 解答： 解：（1）原式=49﹣58=﹣9；‎ ‎（2）原式=19+76﹣22+52=19+76+52+（﹣22）=147+（﹣22）=125；‎ ‎（3）原式=（﹣6）+﹣4+﹣=﹣10+=﹣9；‎ ‎（4）原式=0.5+（﹣）+（+3）+=0+4=4；‎ ‎（5）原式=（﹣0.6）+（﹣7）+（+3.2）+（﹣1）=﹣8.6+3.2=﹣5.4；‎ ‎（6）原式=﹣1.6﹣0.4﹣3+3.2+1.8=﹣5+5=0．‎ 点评： 此题考查了有理数的加减混合运算，熟练掌握运算法则是解本题的关键．‎ ‎　‎ ‎30．一辆汽车沿着一条南北方向的公路来回行驶．某一天早晨从A地出发，晚上到达B地．约定向北为 正，向南为负，当天记录如下：（单位：千米）﹣18.3，﹣9.5，+7.1，﹣14，﹣6.2，+13，﹣6.8，﹣8.5‎ ‎（1）问B地在A地何处，相距多少千米？（2）若汽车行驶每千米耗油0.2升，那么这一天共耗油多少升？‎ 考点： 有理数的加减混合运算．‎ 专题： 计算题．‎ 分析： （1）把所给的数值相加，求出结果，若为正，则说明B在A的北边，若为负，则说明B在A的南边；‎ ‎（2）先求出所有数值绝对值的和，再乘以0.2即可．‎ 解答： 解：（1）﹣18.3﹣9.5+7.1﹣14﹣6.2+13﹣6.8﹣8.5=﹣43.2（千米），‎ 所以B在A地正南方向，相距43.2千米；‎ ‎（2）18.3+9.5+7.1+14+6.2+13+6.8+8.5=83.4（千米），‎ ‎83.4×0.2=16.68（升），‎ 答：一共耗油16.68升．‎ 点评： 本题考查了有理数的加减混合运算，解题的关键是注意理解相反意义的量的含义，耗油量=行使的路程×单位耗油量．‎ ‎　‎ ‎31．从2开始，连续偶数相加，它们和的情况如下表：‎ 加数的个数 和 ‎1 2=1×2‎ ‎2 2+4=6=2×3‎ ‎3 2+4+6=12=3×4‎ ‎4 2+4+6+8=20=4×5‎ ‎… …‎ 观察上面的式子有怎样的规律，并用你发现的规律来计算：‎ ‎（1）2+4+6+8+…+202‎ ‎（2）126+128+130+…+300．‎ 考点： 有理数的混合运算．‎ 专题： 规律型．‎ 分析： 由表中的式子可得和S与数的个数n之间的关系为：S=n（n+1）；‎ ‎（1）首先确定有几个加数，由上述可得规律：加数的个数为最后一个加数÷2，据此解答；‎ ‎（2）把126+128+130+…+300=2+4+6+8+…+300﹣（2+4+6+8+…+124），再进一步利用规律计算即可．‎ 解答： 解：由上面的式子有如下规律：‎ 和S与数的个数n之间的关系为：S=n（n+1）；‎ ‎（1）2+4+6+8+…+202‎ ‎=101×102‎ ‎=10302；‎ ‎（2）126+128+130+…+300‎ ‎=2+4+6+8+…+300﹣（2+4+6+8+…+124）‎ ‎=150×151﹣62×62‎ ‎=22650﹣3906‎ ‎=18744．‎ 点评： 此题考查有理数的混合运算，学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．‎