苏科版八年级上数学期中试题 6页

苏教版八年级数学上册期中考试测试卷一、选择题（共6小题，每小题3分，共18分）1．4的平方根为（）A．2B．C．D．2．下面的图形中，是轴对称图形的是（）ABCD3．下列各组数作为三角形的三边长，其中能构成直角三角形的是（）A．2，3，4B．3，4，5C．4，5，6D．5，6，74．已知等腰三角形的两边长分別为a、b，且a、b满足，则此等腰三角形的底边长为（）A．3或7B．4C．7D．35．下列说法正确的是（）A．无限小数都是无理数B．9的立方根是3C．平方根等于本身的数是0D．数轴上的每一个点都对应一个有理数第6题图6．如图，OP是∠AOB的平分线，点C、D分别在∠AOB的两边OA、OB上，添加下列条件，不能判定△POC≌△POD的选项是（）A．∠OPC=∠OPDB．PC=PDC．PC⊥OA，PD⊥OBD．OC=OD二、填空题（共10小题，每小题3分，共30分）7．比较大小：．8．0.21675精确到百分位的结果是　　　．9．在Rt△ABC中，∠C=90°，D为斜边AB的中点，若AB=10cm，则CD=　　　　cm．10.在镜子中看到电子表显示的时间是，电子表上实际显示的时间为　　． 11．在等腰三角形ABC中，∠A=100º，则∠C=°．12．已知正数x的两个平方根是m+3和2m-15，则正数x＝．第14题图第13题图13．如图，在Rt△ABC中，∠C=90°，AB的垂直平分线交BC于点E，AB=5，AC=3，则△ACE的周长为．14．如图，正方形OABC的边OC落在数轴上，点C表示的数为1，点P表示的数为-1，以P点为圆心，PB长为半径作圆弧与数轴交于点D，则点D表示的数为．15．如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连结AA′，若∠AA′B′=20°，则∠B的度数为°．第15题图第16题图16．如图，△ABC的周长是12，BO、CO分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，则△ABC的面积是　　　．三、解答题(共102分)17．（本题满分8分）求下列各式中的值．（1）（2）18．（本题满分8分）计算：（1）（2） 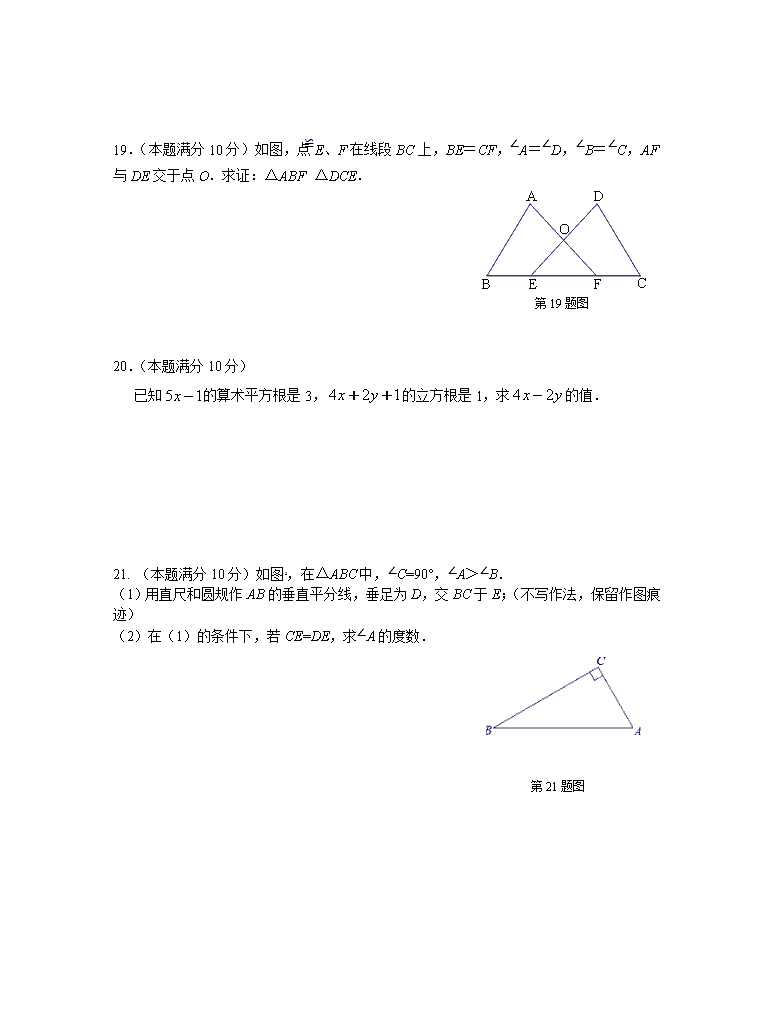第19题图19．（本题满分10分）如图，点E、F在线段BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O．求证：△ABF≌△DCE．20．（本题满分10分）已知的算术平方根是3，的立方根是1，求的值．21.（本题满分10分）如图，在△ABC中，∠C=90°，∠A＞∠B．（1）用直尺和圆规作AB的垂直平分线，垂足为D，交BC于E；（不写作法，保留作图痕迹）（2）在（1）的条件下，若CE=DE，求∠A的度数．第21题图 22．（本题满分10分）已知△ABC中，D为边BC上一点，AB=AD=CD．（1）试说明∠ABC=2∠C；第22题图（2）过点B作AD的平行线交CA的延长线于点E，若AD平分∠BAC，求证AE=AB．23．（本题满分10分）如图，在6×6的正方形网格中，每个小正方形边长都是1，每个小正方形的顶点叫做格点．A、B两格点位置如图所示．（1）在下图正方形网格中找格点C，使△ABC是等腰直角三角形，问：满足条件的点C有个；（2）如图，点D为正方形网格的格点，试求△ABD的面积．．．AB．D第23题图 24．（本题满分10分）如图，△ABC中，∠C=90°，AB=10cm，BC=6cm，若动点P从点C出发，沿线段CA向点A运动，到达A点后停止运动，且速度为每秒2cm，设出发的时间为t秒．（1）当t为何值时，△PBC是等腰三角形；（2）过点P作PH⊥AB，垂足为H，当H为AB中点时，求t的值．第24题图25．（本题满分12分）在小学，我们已经初步了解到，正方形的每个角都是90°，每条边都相等．如图，在正方形ABCD的AD边右侧作直线AQ，且∠QAD=30°，点D关于直线AQ的对称点为E，连接DE、BE，DE交AQ于点G，BE的延长线交AQ于点F．第25题图（1）求证：△ADE是等边三角形；（2）求∠ABE的度数；（3）若AB=4，求FG的长． 26．（本题满分14分）已知，点P是Rt△ABC斜边AB上一动点（不与A、B重合），分别过A、B向直线CP作垂线，垂足分别为E、F，Q为斜边AB的中点．（1）如图1，当点P与点Q重合时，求证：QE=QF；（2）如图2，若AC=BC，求证：BF=AE+EF；（3）在（2）的条件下，若AE=6，QE=，求线段AC的长．第26题图图2图1