八年级下物理课件人教物理八下12-1杠杆课件_人教新课标 19页

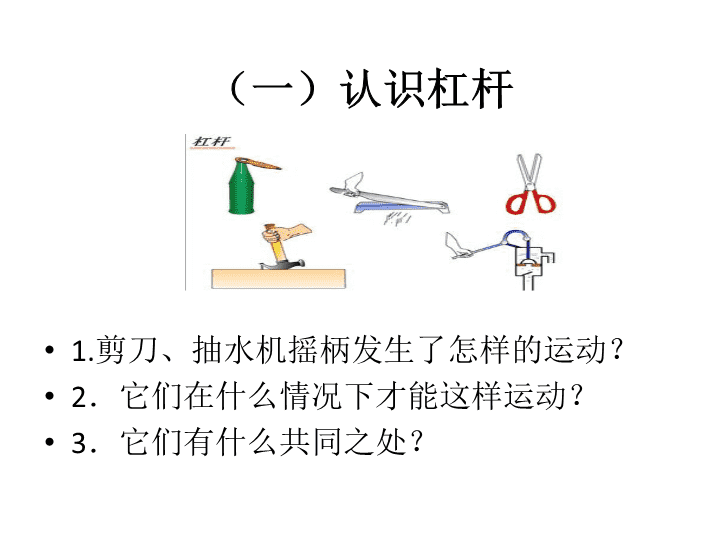
• 中华五千年的文明，留下很多辉煌的历史， 距今2000多年的秦朝，劳动人民在没有先 进器械的条件下，仍然建设出巍峨的宫殿！ 当时人民是如何运送巨大的木材的那？ 新课引入 （一）认识杠杆 • 1.剪刀、抽水机摇柄发生了怎样的运动？ • 2．它们在什么情况下才能这样运动？ • 3．它们有什么共同之处？ 杠杆的五要素 • 杠杆的概念: 一根硬棒，力的作用下能绕着固定点 转动，这根硬棒就是杠杆。 • 1．支点：杠杆转动后绕其转动的点。用点o标出 • 2．动力、阻力：画出力的示意图，（大小、方向、 作用点） • 3．力作用线：力的方向所在的直线 • 4．力臂：从支点到（动、阻）力的作用线的距离。 • 类比数学中点到直线的距离： • 数学：点到 直线 垂线段的长度 • 物理：支点到力的作用线的距离 • 方法：支点向力的作用线画垂线段 【反馈练习】要求用直尺三角板规范画出力臂 F2 B O A F1 • 【方法口诀】 • 一找支点---辨认杠杆，找出支点、动 力和阻力 • 二描线---过力的作用点沿力的方向画 直线 • 三画垂线---由支点向作用线画垂线段 • 四标签---用大括号将力臂括上，并标 上符号。 （二）杠杆的平衡条件探究 • 【问题设疑】 • 杠杆平衡时，动力、动力臂和阻力、阻力臂之间可能存在 着怎样的关系呢？请同学们大胆猜想！ • 学生生猜想： • 1：动力+动力臂=阻力+阻力臂； • 2：动力-动力臂=阻力-阻力臂 ； • 3：动力×动力臂=阻力×阻力臂； • 4：动力/动力臂=阻力/阻力臂。 • 【引导点拨】 • 猜想1、2合理吗？，因此，我们主要检验猜想3、4是否合 理。 • 【制定计划、设计实验】 • （1）实验目的：研究杠杆平衡的条件。 • （2）实验器材：杠杆和支架、钩码、刻度尺、线 • （3）实验步骤： • ①调节杠杆两端的螺母，使杠杆在水平位置平衡。 • ②在杠杆两边挂上不同数量的钩码，调节位置， 使杠杆重新平衡。 • ③把支点右边的钩码重当作动力F1，支点左边的 钩码重当作阻力F2，量出动力臂L1和阻力臂L2， 将各数值填入表格中。 • ④改变钩码数量或位置，重复上面的步骤，得出 三组数据。 实验次数 动力F1 动力臂、L1/cm 阻力F2 阻力臂L2/cm 1 2 3 得出结论： 杠杆平衡条件是动力×动力臂=阻力×阻力臂即F1 l 1= F2 l 2 • 【典例剖析】小小弹簧秤，巧称大象重 求大象的质量是多少？ • 【反馈练习】 • 1.两个小孩坐在跷跷板上，恰好处于平衡，此时 • A.两个小孩重力一定相等 • B.两个小孩到支点的距离一定相等 • C.两个小孩质量一定相等 • D.两边的力臂与小孩重力的乘积相等 • 2.杠杆平衡时，动力为10N，阻力为40N， 动力臂为0.4m 求阻力臂。 • 3.如图所示为使杠杆平衡，F1、F2、F3 三次分别作用在A点， 其中______最小。 • D F1L1=F2L2 10N0.4m =40N  L2解之得，L2=0.1m F3 • （三）杠杆的应用及分类 1.镊子 2.起子 3.缝纫机踏板 4.天平 6.羊角锤5.钓鱼竿 • 【归纳总结】 • 根据杠杆平衡条件：F1 l 1= F2 l 2 • 则可以把杠杆分成三类: • 1.若l 1＞l 2，则F1 F2 ，省力杠杆（省力费 距离），如上图中的 . • 2.若l 1= l 2，则F1 F2 ，等臂杠杆（不省力 也不距离），如上图中的 . • 3.若l 1＜l 2，则F1 F2，费力杠杆（费力省 距离），如上图中的 . 答案：1.＜ 2、6 2.＝ 4 ＞ 1、3、5、7。 【课堂小总】 1.一只山羊和一只白兔在野外觅食，它俩同时发现了一只胡萝卜， 就如何分配时争执不休，它俩便找来聪明的狐狸来平均分配这只 萝卜。狐狸灵机一动，找到一块石头，将萝卜放在上面，如图所 示，此时正好平衡，它便从支点处切开，山羊和白兔各食一端， 皆大欢喜地走了，你认为狐狸这样分萝卜合理吗？为什么？ 答：不合理。根据杠杆平衡条件可知： 力臂大的那端，受到的重力小，质量 也就小，力臂短的那端，受到的重力 大，质量也就大，所以，左端粗而短， 质量大。分到这端的也就占了便宜。 课堂检测 2.如图所示，曲杆AOBC的自重不计， O为支点，AO=60cm，OB=40cm， BC=30cm,要使曲杆在图中位置平衡， 请作出最小的力F的示意图及其力臂 L。 3.如图所示，有一粗细不均的圆木放在水平地面上，其长度为10m,若略抬起 圆木大头A点时，需用200N的力，若抬起圆木小头B时，需用100N的力，则 圆木的重为多少N？ A B 解： 设圆木的重力为G，重心作 用在距A端L m处，则离了端 的距离为（10-L）m. 若以A为支点，略抬起B端时，根据杠杆平衡条件有： 100N×10m=GL 若以B为支点，略抬起A端时，根据杠杆平衡条件有： 200N×10m=G(10-L) (1) (2) 解（1）（2）两式可得：圆木重为G=300N。 答：圆木重为G=300N。