八年级数学上册第十四章整式的乘法与因式分解14-2乘法公式14-2-2完全平方公式教学课件新版 人教版 28页

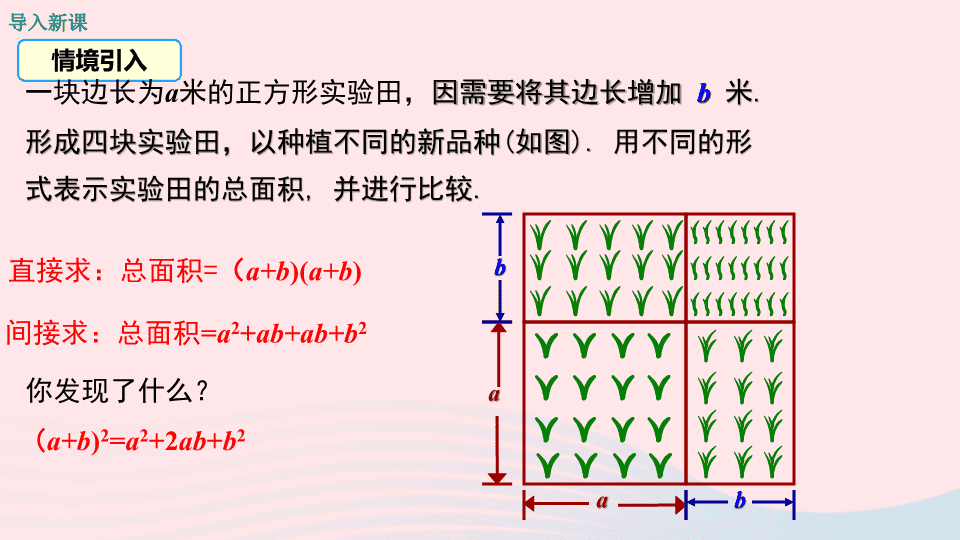
14.2.2 完全平方公式 第十四章 整式的乘法与因式分解 14.2 乘法公式 学习目标 1. 理解并掌握 完全平方 公式的推导过程、结构特点、 几何解释 . （重点） 2. 灵活应用完全平方公式进行计算 . （难点） 导入新课 情境引入 一块边长为 a 米的正方形实验田， 因需要将其边长增加 b 米 . 形成四块实验田，以种植不同的新品种 ( 如图 ). 用不同的形式表示实验田的总面积 , 并进行比较 . 直接求：总面积 = （ a+b )( a+b ) 间接求：总面积 = a 2 + ab+ab+b 2 你发现了什么？ （ a+b ) 2 = a 2 +2 ab + b 2 a a b b 讲授新课 完全平方公式 一 问题 1 计算下列多项式的积，你能发现什么规律？ （ 1 ） （ p +1) 2 =( p +1)( p +1)= . p 2 +2 p +1 （ 2 ） （ m +2) 2 =( m +2)( m +2)= . m 2 +4 m +4 （ 3 ） （ p -1) 2 =( p -1)( p -1)= . p 2 -2 p +1 （ 4 ） （ m -2) 2 =( m -2)( m -2)= . m 2 -4 m +4 问题 2 根据你发现的规律，你能 写出下列式子的 答案吗？ （ a + b ) 2 = . a 2 +2 ab + b 2 （ a - b ) 2 = . a 2 -2 ab + b 2 合作探究 知识要点 完全平方公式 （ a + b ) 2 = . a 2 +2 ab + b 2 （ a - b ) 2 = . a 2 -2 ab + b 2 也就是说， 两个数的和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的 2 倍 . 这两个公式叫做（乘法的） 完全平方公式 . 简记为： “首平方，尾平方，积的 2 倍放中间” 问题 3 你能根据图 1 和图 2 中的面积说明完全平方公式吗 ? b a a b b a b a 图 1 图 2 几何解释 : a a b b = + + + a 2 ab ab b 2 （ a + b ) 2 = . a 2 +2 ab + b 2 和的完全平方公式： a 2 − a b − b ( a − b ) = a 2 −2 a b + b 2 . = ( a − b ) 2 a − b a − b a a a b b ( a − b ) b b ( a − b ) 2 几何解释 : （ a - b ) 2 = . a 2 -2 ab + b 2 差的完全平方公式： ( a + b ) 2 = a 2 +2 ab + b 2 . ( a - b ) 2 = a 2 - 2 ab + b 2 . 问题 4 观察下面两个完全平方式，比一比，回答下列问题： 1. 说一说积的次数和项数 . 2. 两个完全平方式的积有相同的项吗？与 a , b 有 什么关系？ 3. 两个完全平方式的积中不同的是哪一项？与 a , b 有什么关系？它的符号与什么有关？ 公式特征： 4. 公式中的字母 a ， b 可以表示数，单项式和多项式 . 1. 积为二次三项式； 2. 积中两项为两数的平方和； 3. 另一项是两数积的 2 倍，且与 两数 中间的符号相同 . 想一想： 下面各式的计算是否正确？如果不正确 , 应当怎样改正？ ( 1 ) ( x + y ) 2 = x 2 + y 2 (2)( x - y ) 2 = x 2 - y 2 (3) (- x + y ) 2 = x 2 +2 xy + y 2 (4) (2 x + y ) 2 =4 x 2 +2 xy + y 2 × × × × ( x + y ) 2 = x 2 +2 xy + y 2 ( x - y ) 2 = x 2 -2 xy + y 2 (- x + y ) 2 = x 2 - 2 xy + y 2 (2 x + y ) 2 =4 x 2 + 4 xy + y 2 典例精析 例 1 运用完全平方公式计算： 解 : (4 m + n ) 2 = =16 m 2 (1)(4 m + n ) 2 ； ( a + b ) 2 = a 2 + 2 ab + b 2 (4 m ) 2 +2•(4 m ) • n + n 2 +8 mn + n 2 ； ( a - b ) 2 = a 2 - 2 ab + b 2 y 2 = y 2 - y + 解 ： = + -2 • y • (2) 利用完全平方公式计算： (1)(5 － a ) 2 ； (2)( － 3 m － 4 n ) 2 ； (3)( － 3 a ＋ b ) 2 . 针对训练 (3)( － 3 a ＋ b ) 2 ＝ 9 a 2 － 6 ab ＋ b 2 . 解： (1)(5 － a ) 2 ＝ 25 － 10 a ＋ a 2 ； (2)( － 3 m － 4 n ) 2 ＝ 9 m 2 ＋ 24 mn ＋ 16 n 2 ； (1) 102 2 ； 解： 102 2 = (100+2) 2 =10000+400+4 =10404. (2) 99 2 . 99 2 = (100 –1) 2 =10000 - 200+1 =9801. 例 2 运用完全平方公式计算： 方法总结： 运用完全平方公式进行简便计算，要熟记完全平方公式的特征，将原式转化为能利用完全平方公式的形式． 利用乘法公式计算： (1)98 2 － 101×99 ； (2)2016 2 － 2016×4030 ＋ 2015 2 . 针对训练 ＝ (2016 － 2015) 2 ＝ 1. 解： (1) 原式＝ (100 － 2) 2 － (100 ＋ 1)(100 － 1) ＝ 100 2 － 400 ＋ 4 － 100 2 ＋ 1 ＝－ 395 ； (2) 原式＝ 2016 2 － 2×2016×2015 ＋ 2015 2 例 3 已知 x － y ＝ 6 ， xy ＝－ 8. 求 : (1) x 2 ＋ y 2 的值； (2)( x + y ) 2 的值 . ＝ 36 － 16=20 ； 解： (1)∵ x － y ＝ 6 ， xy ＝－ 8 ， ( x － y ) 2 ＝ x 2 ＋ y 2 － 2 xy ， ∴ x 2 ＋ y 2 ＝ ( x － y ) 2 ＋ 2 xy (2)∵ x 2 ＋ y 2 ＝ 20 ， xy ＝－ 8 ， ∴( x + y ) 2 ＝ x 2 ＋ y 2 ＋ 2 xy ＝ 20 － 16 ＝ 4. 方法总结： 本题要熟练掌握完全平方公式的变式： x 2 ＋ y 2 ＝( x － y ) 2 ＋2 xy ＝( x + y ) 2 －2 xy , ( x － y ) 2 ＝( x + y ) 2 － 4 xy . 添括号法则 二 a +( b + c ) = a + b + c ; a - ( b + c ) = a - b – c . a + b + c = a + ( b + c ) ; a – b – c = a – ( b + c ) . 去括号 把上面两个等式的左右两边反过来，也就添括号： 添括号时 , 如果括号前面是 正 号 , 括到括号里的各项都 不变 号 ; 如果括号前面是 负 号 , 括到括号里的各项都 改变 符号（简记为“ 负变正不变 ”） . 知识要点 添括号法则 例 5 运用乘法公式计算 : (1) ( x +2 y -3)( x -2 y +3) ; (2) ( a+b+c ) 2 . 原式 =[ x +(2 y –3)][ x -(2 y -3)] 解 : (1) 典例精析 (2) 原式 = [( a+b )+ c ] 2 = x 2 -(2 y -3) 2 = x 2 -(4 y 2 -12 y +9) = x 2 -4 y 2 +12 y -9. = ( a+b ) 2 +2( a+b ) c + c 2 = a 2 +2 ab + b 2 +2 ac +2 bc + c 2 . 方法总结： 第 1 小题选用平方差公式进行计算，需要分组 . 分组方法是“符号相同的为一组，符号相反的为另一组” . 第 2 小题要把其中两项看成一个整体，再按照完全平方公式进行计算 . 计算： (1)( a － b ＋ c ) 2 ； (2)(1 － 2 x ＋ y )(1 ＋ 2 x － y ) ． 针对训练 ＝ 1 － 4 x 2 ＋ 4 xy － y 2 . 解： (1) 原式＝ [( a － b ) ＋ c ] 2 ＝ ( a － b ) 2 ＋ c 2 ＋ 2( a － b ) c ＝ a 2 － 2 ab ＋ b 2 ＋ c 2 ＋ 2 ac － 2 bc ； (2) 原式＝ [1 ＋ ( － 2 x ＋ y )][1 － ( － 2 x ＋ y )] ＝ 1 2 － ( － 2 x ＋ y ) 2 当堂练习 2. 下列计算结果为 2 ab － a 2 － b 2 的是 ( ) A ． ( a － b ) 2 B ． ( － a － b ) 2 C ．－ ( a ＋ b ) 2 D ．－ ( a － b ) 2 1. 运用乘法公式计算 ( a -2 ) 2 的结果是（　　） A． a 2 -4 a +4 B． a 2 -2 a +4 C． a 2 -4 D． a 2 -4 a -4 A D 3. 运用完全平方公式计算 : (1) (6 a +5 b ) 2 =_______________ ； (2) (4 x -3 y ) 2 =_______________ ； (3) (2 m -1) 2 =_______________ ； (4)(-2 m -1) 2 =_______________ . 36 a 2 +60 ab +25 b 2 16 x 2 -24 xy +9 y 2 4 m 2 +4 m +1 4 m 2 -4 m +1 4. 由完全平方公式可知： 3 2 ＋ 2×3×5 ＋ 5 2 ＝ (3 ＋ 5) 2 ＝ 64 ，运用这一方法计算： 4.321 2 ＋ 8.642×0.679 ＋ 0.679 2 ＝ ________ ． 25 5. 计算 (1)(3 a ＋ b － 2)(3 a － b ＋ 2) ； ( 2 )( x － y － m ＋ n )( x － y ＋ m － n )． (2) 原式＝ [( x － y ) － ( m － n )][( x － y ) ＋ ( m － n )] 解： (1) 原式＝ [3 a ＋ ( b － 2)][3 a － ( b － 2)] ＝ (3 a ) 2 － ( b － 2) 2 ＝ 9 a 2 － b 2 ＋ 4 b － 4. 　 ＝ ( x － y ) 2 － ( m － n ) 2 ＝ x 2 － 2 xy ＋ y 2 － m 2 ＋ 2 mn － n 2 . 6. 若 a+b =5, ab =-6, 求 a 2 + b 2 , a 2 - ab + b 2 . 7. 已知 x+y =8, x-y =4, 求 xy . 解： a 2 + b 2 = （ a+b ) 2 -2 ab =5 2 -2×(-6)=37 ； a 2 - ab + b 2 = a 2 + b 2 - ab =37-(-6)=43. 解： ∵ x+y =8, ∴( x+y ) 2 =64, 即 x 2 + y 2 +2 xy =64①; ∵ x - y =4, ∴( x-y ) 2 =16, 即 x 2 + y 2 -2 xy =16②; 由 ① -② 得 4 xy =48 ∴ xy =12. 课堂小结 完全平方公式 法则 注意 ( a±b ) 2 = a 2 ± 2 ab+b 2 1. 项数、符号、字母及其指数 2. 不能直接应用公式进行计算的式子，可能需要先添括号变形成符合公式的要求才行 常用 结论 3. 弄清完全平方公式和平方差公式不同（从公式结构特点及结果两方面） a 2 + b 2 =( a+b ) 2 -2 ab =( a-b ) 2 +2 ab ; 4 ab =( a+b ) 2 -( a-b ) 2 .