- 118.50 KB
- 2021-10-26 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
1.1等腰三角形
课题
1.1等腰三角形(1)
课型
讲授课
教学目标
1、 理解作为证明基础的几条公理的内容,应用这些公理证明等腰三角形的性质定理;
2、经历“探索-发现-猜想-证明”的过程,让学生进一步体会证明是探索活动的自然延续和必要发展,发展学生的初步的演绎逻辑推理的能力
3、启发引导学生体会探索结论和证明结论,及合情推理与演绎的相互依赖和相互补充的辩证关系
重点
探索证明等腰三角形性质定理的思路与方法,掌握证明的基本要求和方法;
难点
明确推理证明的基本要求如明确条件和结论,能否用数学语言正确表达等。
教学用具
多媒体课件
教学环节
复习
复习引入:
1.三角形全等的判定:
两边及其夹角对应相等的两个三角形全等; (SAS)
两角及其夹边对应相等的两个三角形全等; (ASA)
三边对应相等的两个三角形全等. (SSS)
两角及其中一角的对边对应相等的两个三角形全等(AAS)
2.全等三角形的性质:
全等三角形的对应边相等,对应角相等.
3.等腰三角形的性质
等腰三角形的两个底角相等
等腰三角形的两腰相等
等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合(三线合一).
4.等腰三角形是轴对称图形
4
课 程 讲 授
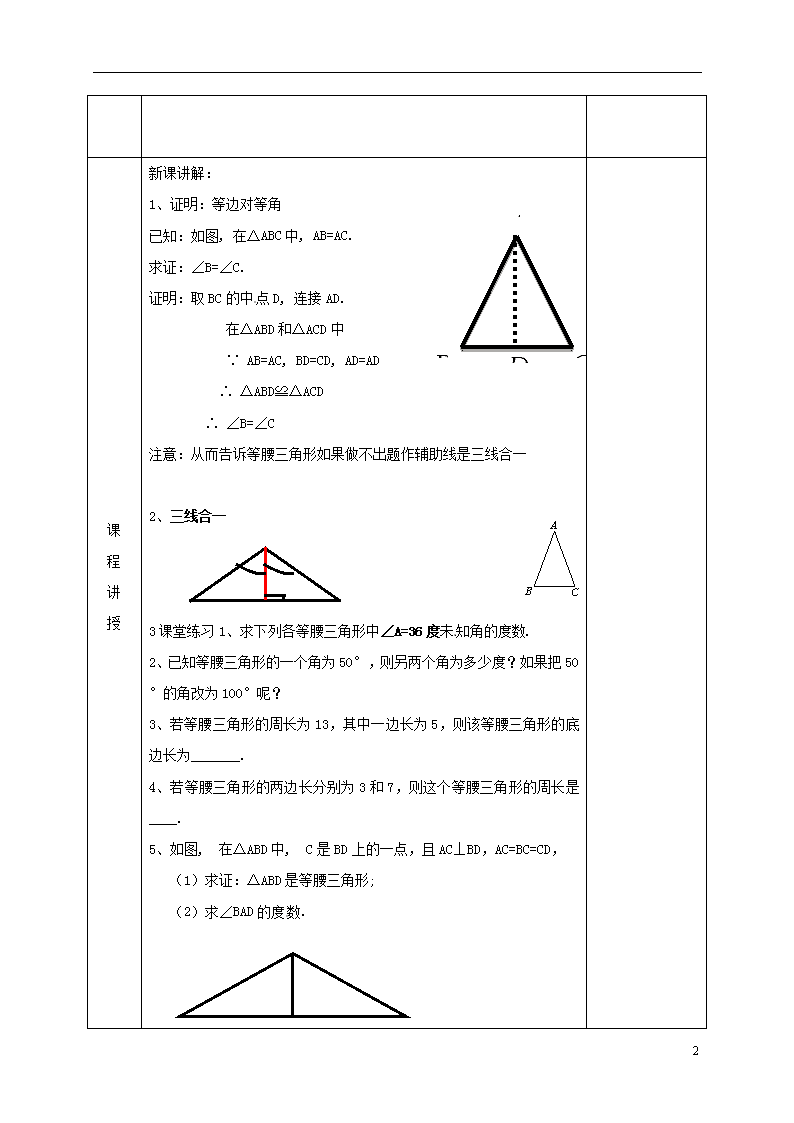
新课讲解:
1、证明:等边对等角
已知:如图, 在△ABC中, AB=AC.
求证:∠B=∠C.
证明:取BC的中点D, 连接AD.
在△ABD和△ACD中
C
B
A
D
∵ AB=AC, BD=CD, AD=AD
∴ △ABD≌△ACD
∴ ∠B=∠C
注意:从而告诉等腰三角形如果做不出题作辅助线是三线合一
2、三线合一
A
C
B
D
1
2
3课堂练习1、求下列各等腰三角形中∠A=36度未知角的度数.
2、已知等腰三角形的一个角为50°,则另两个角为多少度?如果把50°的角改为100°呢?
3、若等腰三角形的周长为13,其中一边长为5,则该等腰三角形的底边长为_______.
4、若等腰三角形的两边长分别为3和7,则这个等腰三角形的周长是 ____.
5、如图, 在△ABD中, C是BD上的一点,且AC⊥BD,AC=BC=CD,
(1)求证:△ABD是等腰三角形;
(2)求∠BAD的度数.
A
B
D
C
4
小结
等腰三角形的性质定理的证明
作业布置
板书设计
4
课后反思
4
相关文档
- 最新湘教版初中地理八年级上册《32021-10-2616页
- 最新人教版初中地理八年级下册《72021-10-2614页
- 初中地理会考复习知识点整理(45页)2021-10-2645页
- 2020年华东师大版数学初中八年级上2021-10-2620页
- 商务星球初中地理八年级上册《1第12021-10-2627页
- 最新中图版初中地理八年级上册《32021-10-2618页
- 最新人教版初中地理八年级下册《72021-10-2630页
- 初中数学八年级上册第十四章整式的2021-10-262页
- 初中数学八年级上册第十四章整式的2021-10-262页
- 最新中图版初中地理八年级下册《72021-10-2619页