2020八年级数学上册期末综合自我评价练习（新版）浙教版 14页

期末综合自我评价 一、选择题(每小题2分，共20分)‎ ‎1．下面四个标志中，是轴对称图形的是(D)‎ ‎2．在平面直角坐标系中，点P(3，－2)关于y轴的对称点在(C)‎ A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 ‎3．使不等式x－2≥－3与2x＋3＜5同时成立的x的整数值是(C)‎ A. －2，－1，0 B. 0，1‎ C. －1，0 D. 不存在 ‎4．一个三角形的两边长分别为‎3 cm和‎7 cm，则此三角形第三边长可能是(C)‎ A．‎3 cm B．‎4 cm ‎ C．‎7 cm D．‎‎11 cm ‎5．为了举行班级晚会，小张同学准备去商店购买20个乒乓球做道具，并买一些乒乓球拍做奖品．已知乒乓球每个1.5元，球拍每个25元．如果购买金额不超过200元，且要求买的球拍尽可能多，那么小张同学应该买的球拍的个数是(B)‎ A. 5 B. 6 ‎ C. 7 D. 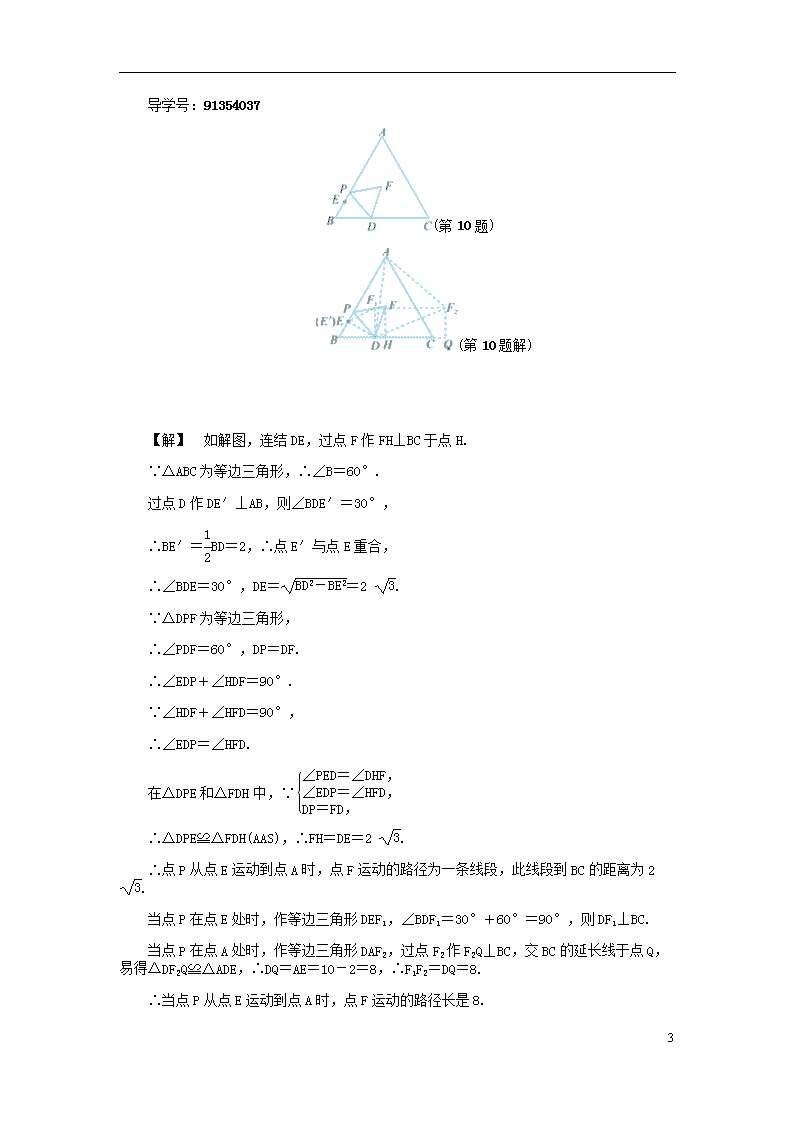8‎ ‎6．如图，在△ABC中，∠ACB＝90°，∠ABC＝60°，BD平分∠ABC，P是BD的中点．若AD＝6，则CP的长为(A)‎ A. 3 B. 3.5 ‎ C. 4 D. 4.5‎ ‎(第6题)‎ ‎　　(第7题)‎ 14‎ ‎7．如图，把一张长方形纸片ABCD沿EF折叠后，点A落在CD边上的点A′处，点B落在点B′处．若∠2＝40°，则图中∠1的度数为(A)‎ A. 115° B. 120° ‎ C. 130° D. 140°‎ ‎【解】　由折叠可得∠1＝∠EFB′，∠B′＝∠B＝90°.‎ ‎∵∠2＝40°，∴∠CFB′＝90°－40°＝50°.‎ ‎∵∠1＋∠EFB′－∠CFB′＝180°，‎ ‎∴∠1＋∠1－50°＝180°，解得∠1＝115°.‎ ‎8．在平面直角坐标系中，将直线l1：y＝－2x－2平移后，得到直线l2：y＝－2x＋4，则下列平移作法中，正确的是(A)‎ A. 将直线l1向右平移3个单位 B. 将直线l1向右平移6个单位 C. 将直线l1向上平移2个单位 D. 将直线l1向上平移4个单位 ‎【解】　∵将直线l1：y＝－2x－2平移后，得到直线l2：y＝－2x＋4，‎ ‎∴－2(x＋a)－2＝－2x＋4或－2x－2＋b＝－2x＋4，解得a＝－3，b＝6.‎ ‎∴应将直线l1向右平移3个单位或向上平移6个单位．故选A.‎ ‎9．已知A(x1，y1)，B(x2，y2)为一次函数y＝2x＋1的图象上的两个不同的点，且x1x2≠0.若M＝，N＝，则M与N的大小关系是(C)‎ A．M>N B．Ma＋1(a≠－1)可以变形为x<1，那么a的取值范围是a<－1．‎ ‎13．在△ABC中，AB＝15，AC＝13，高AD＝12，则BC的长为14或4．‎ ‎【解】　如解图①.‎ 由勾股定理，得BD＝＝9，CD＝＝5，∴BC＝BD＋CD＝14.‎ ‎(第13题解)‎ 如解图②，同理可得BD＝9，CD＝5，‎ ‎∴BC＝BD－CD＝4.‎ ‎(第14题)‎ ‎14．如图，△ABC和△DCE都是边长为4的等边三角形，点B，C，E在同一条直线上，连结BD，则BD的长为4_．‎ ‎【解】　∵△ABC和△DCE都是边长为4的等边三角形，‎ ‎∴CB＝CD，‎ ‎∴∠BDC＝∠DBC＝30°.‎ 又∵∠CDE＝60°，∴∠BDE＝90°.‎ 在Rt△BDE中，DE＝4，BE＝8，‎ ‎∴BD＝＝＝4 .‎ ‎15．有学生若干人，住若干间宿舍．若每间住4人，则有20人无法安排住宿；若每间住8人，则最后有一间宿舍不满也不空，则学生有__44__人．‎ ‎【解】　设共有x间宿舍，则学生有(4x＋20)人．‎ 14‎ 由题意，得0<4x＋20－8(x－1)<8，‎ 解得53＋a。‎ 解不等式②，得x<1.‎ ‎∵不等式组无解，‎ ‎∴3＋a≥1，即a≥－2.‎ ‎17．已知一次函数y＝2x＋‎2a与y＝－x＋b的图象都经过点A(－2，a)，且与x轴分别交于B，C两点，则△ABC的面积为__12__．‎ ‎【解】　把点A(－2，a)的坐标分别代入y＝2x＋‎2a，y＝－x＋b，得∴ ‎∴y＝2x＋8，y＝－x＋2.‎ 易得点B(－4，0)，C(2，0)，‎ ‎∴S△ABC＝×[2－(－4)]×4＝12.‎ ‎18．如图，在四边形ABCD中，对角线AC，BD相交于点E，∠DAB＝∠CDB＝90°，∠ABD＝45°，∠DCA＝30°，AB＝，则AE＝__2__．‎ ‎,(第18题))　　　,(第18题解))‎ ‎【解】　如解图，过点A作AF⊥BD于点F.‎ ‎∵∠DAB＝90°，∠ABD＝45°，‎ ‎∴△ABD为等腰直角三角形，‎ ‎∴AF为BD边上的中线，‎ ‎∴AF＝BD.‎ ‎∵AD＝AB＝，‎ 14‎ ‎∴根据勾股定理，得BD＝＝2，‎ ‎∴AF＝.‎ ‎∵∠CDE＝90°＝∠AFE，∴CD∥AF，‎ ‎∴∠EAF＝∠DCA＝30°，∴EF＝AE.‎ 设EF＝x，则AE＝2x.‎ 根据勾股定理，得x2＋3＝4x2，‎ 解得x＝1(负值舍去)．‎ ‎∴AE＝2.‎ ‎(第19题)‎ ‎19．如图，两把完全相同的含30°角的三角尺叠放在一起，且∠DAB＝30°.有下列结论：①AF⊥BC；②△ADG≌△ACF；③O为BC的中点；④AG∶GE＝∶4.其中正确的是①②③(填序号)．‎ ‎【解】　由题意，得△ADE≌△ACB，‎ ‎∴∠D＝∠C，∠E＝∠B，∠DAE＝∠CAB＝90°，AD＝AC，‎ ‎∴∠DAE－∠BAE＝∠CAB－∠BAE，‎ ‎∴∠CAF＝∠DAG＝30°.‎ ‎∵∠B＝∠30°，∴∠D＝∠C＝60°，‎ ‎∴∠AGD＝∠AFC＝90°，∴AF⊥BC，故①正确．‎ 在△ADG和△ACF中，‎ ‎∵ ‎∴△ADG≌△ACF(ASA)，故②正确．‎ ‎∴AG＝AF.‎ 连结AO.‎ 在Rt△AGO和Rt△AFO中，‎ ‎∵ ‎∴Rt△AGO≌Rt△AFO(HL)．‎ 14‎ ‎∴∠GAO＝∠FAO.‎ ‎∵∠DAE＝90°，∠DAB＝30°，‎ ‎∴∠GAF＝60°，∴∠GAO＝∠FAO＝30°，‎ ‎∴∠AOC＝∠OAB＋∠B＝60°，OA＝OB，‎ ‎∴△AOC是等边三角形，∴OC＝OA＝OB，‎ ‎∴O为BC的中点，故③正确．‎ ‎∵∠E＝30°，∠AGE＝90°，∴AE＝2AG.‎ 设AG＝a，则AE＝‎2a.由勾股定理，得GE＝a，‎ ‎∴AG∶GE＝a∶a＝1∶，故④错误．‎ 综上所述，正确的是①②③.‎ ‎20．已知一次函数y＝x－15的图象与x轴，y轴分别交于点A，B，O为坐标原点，则在△OAB内部(包括边界)，纵坐标、横坐标都是整数的点(整点)共有__106__个．导学号：91354038‎ ‎【解】　易得点A(12，0)，B(0，－15)．‎ 设当x＝n时，在△OAB内部且不在x轴上的整点个数为an.‎ 易得a1＝13，a2＝12，a3＝11，a4＝10，a5＝8，a6＝7，a7＝6，a8＝5，a9＝3，a10＝2，a11＝1.‎ 在坐标轴上的点共有15＋1＋12＝28(个)．‎ ‎∴整点共有13＋12＋11＋10＋8＋7＋6＋5＋3＋2＋1＋28＝106(个)．‎ 三、解答题(共50分)‎ ‎21．(6分)(1)解不等式组：并把它的解在数轴上表示出来．‎ ‎【解】　解第一个不等式，得x≤2.‎ 解第二个不等式，得x＞－1.‎ ‎∴此不等式组的解为－1＜x≤2.‎ 在数轴上表示如解图①所示．‎ ‎(第21题解①)‎ 14‎ ‎(2)解不等式组：并把它的解在数轴上表示出来．‎ ‎【解】　解第一个不等式，得x＜4.‎ 解第二个不等式，得x≥－1.‎ ‎∴此不等式组的解为－1≤x＜4.‎ 在数轴上表示如解图②所示．‎ ‎,(第21题解②))‎ ‎(第22题)‎ ‎22．(6分)如图，已知在△ABC中，AB＝AC，BC＝6，AM平分∠BAC，D为AC的中点，E为BC延长线上的一点，且CE＝BC.‎ ‎(1)求ME的长．‎ ‎(2)求证：△DMC是等腰三角形．‎ ‎【解】　(1)∵AB＝AC，AM平分∠BAC，‎ ‎∴BM＝CM＝BC＝CE＝3，‎ ‎∴ME＝MC＋CE＝3＋3＝6.‎ ‎(2)∵AB＝AC，AM平分∠BAC，∴AM⊥BC.‎ ‎∵D为AC的中点，∴DM＝DC，‎ ‎∴△DMC是等腰三角形．‎ ‎23．(6分)如图，已知∠CDA＝∠AEB＝90°，且CD＝AE，AD＝BE.‎ ‎(第23题)‎ ‎(1)求证：AC＝BA.‎ ‎(2)△ABC是什么三角形？请说明理由．‎ 14‎ ‎(3)如果AM⊥BC，那么AM＝BC吗？请说明理由．‎ ‎【解】　(1)在△ACD和△BAE中，‎ ‎∵CD＝AE，∠CDA＝∠AEB＝90°，AD＝BE，‎ ‎∴△ACD≌△BAE(SAS)．∴AC＝BA.‎ ‎(2)△ABC是等腰直角三角形．理由如下：‎ 由(1)知△ACD≌△BAE，‎ ‎∴AC＝BA，∠CAD＝∠ABE，‎ ‎∴∠BAC＝180°－∠CAD－∠BAE＝180°－∠ABE－∠BAE＝180°－90°＝90°.‎ ‎∴△ABC为等腰直角三角形．‎ ‎(3)AM＝BC.理由如下：‎ ‎∵△ABC为等腰直角三角形，且AM⊥BC，‎ ‎∴BM＝CM，∴AM＝BC.‎ ‎24．(10分)某经销商从市场得知如下信息：‎ A品牌手表 B品牌手表 进价(元/块)‎ ‎700‎ ‎100‎ 售价(元/块)‎ ‎900‎ ‎160‎ 他计划用4万元资金一次性购进这两种品牌手表100块，设该经销商购进A品牌手表x块，这两种品牌手表全部销售完后获得的利润为y元．‎ ‎(1)试写出y与x之间的函数表达式．‎ ‎(2)若要求全部销售完后获得的利润不少于1.26万元，该经销商有哪几种进货方案？‎ ‎(3)选择哪种进货方案，该经销商获得的利润最大？最大利润是多少元？‎ ‎【解】　(1)由题意，得y＝(900－700)x＋(160－100)(100－x)＝140x＋6000.‎ ‎∵700x＋100(100－x)≤40000，‎ 解得x≤50，即y＝140x＋6000(0≤x≤50)．‎ ‎(2)令y≥12600，则140x＋6000≥12600，‎ 解得x≥47.‎ 14‎ 又∵x≤50，∴47≤x≤50，‎ ‎∴x可取得48，49，50.‎ ‎∴经销商有三种进货方案：‎ 方案一，进A品牌手表48块，B品牌手表52块；‎ 方案二，进A品牌手表49块，B品牌手表51块；‎ 方案三，进A品牌手表50块，B品牌手表50块．‎ ‎(3)∵y＝140x＋6000，140>0，‎ ‎∴y随x增大而增大，‎ ‎∴当x＝50时，y取得最大值．‎ 又∵140×50＋6000＝13000(元)，‎ ‎∴选择方案三，即进A品牌手表50块，B品牌手表50块时，经销商获得的利润最大，最大利润是13000元．‎ ‎25．(10分)【问题提出】‎ 用n根相同的木棒搭一个三角形(木棒无剩余)，能搭成多少种不同的等腰三角形？‎ ‎【问题探究】‎ 不妨假设能搭成m种不同的等腰三角形，为探究m与n之间的关系，我们可以先从特殊入手，通过试验、观察、类比、最后归纳、猜测得出结论．‎ ‎【探究一】‎ ‎(1)用3根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？‎ 此时，显然只能搭成一种等腰三角形．‎ 所以，当n＝3时，m＝1.‎ ‎(2)用4根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？‎ 只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形．‎ 所以，当n＝4时，m＝0.‎ ‎(3)用5根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？‎ 若分成1根木棒、1根木棒和3根木棒，则不能搭成三角形；若分成2根木棒、2根木棒和1根木棒，则能搭成一种等腰三角形．‎ 所以，当n＝5时，m＝1.‎ ‎(4)用6根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？‎ 若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形；若分成2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形．‎ 14‎ 所以，当n＝6时，m＝1.‎ 综上所述，可得表如下：‎ n ‎3‎ ‎4‎ ‎5‎ ‎6‎ m ‎1‎ ‎0‎ ‎1‎ ‎1‎ ‎【探究二】‎ ‎(1)用7根相同的木棒搭一个三角形，能搭成多少种不同的三角形(仿照上述探究方法，写出解答过程，并将结果填在下表中)?‎ n ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎…‎ m ‎2‎ ‎1‎ ‎2‎ ‎2‎ ‎…‎ ‎(2)用8根、9根、10根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形(只需把结果填在上表中)?‎ 你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究……‎ ‎【问题解决】‎ 用n根相同的木棒搭一个三角形(木棒无剩余)，能搭成多少种不同的等腰三角形(设n分别等于4k－1，4k，4k＋1，4k＋2，其中k是正整数，把结果填在下表中)?‎ n ‎4k－1‎ ‎4k ‎4k＋1‎ ‎4k＋2‎ ‎…‎ m ‎…‎ ‎【问题应用】‎ 用2018根相同的木棒搭一个三角形(木棒无剩余)，能搭成多少种不同的等腰三角形(写出解答过程)?‎ ‎【解】　【探究二】‎ ‎(1)若分成1根木棒、1根木棒和5根木棒，则不能搭成三角形；若分成2根木棒、2根木棒和3根木棒，则能搭成一种等腰三角形；若分成3根木棒、3根木棒和1根木棒，则能搭成一种等腰三角形．‎ 所以，当n＝7时，m＝2.‎ ‎(2)同(1)可得：当n＝8时，m＝1；当n＝9时，m＝2；当n＝10时，m＝2.‎ ‎【问题解决】‎ 由规律，补充表如下： ‎ n ‎4k－1‎ ‎4k ‎4k＋1‎ ‎4k＋2‎ ‎…‎ m k k－1‎ k k ‎…‎ ‎【问题应用】‎ ‎∵2018÷4＝504……2，‎ 14‎ ‎∴用2018根相同的木棒搭一个三角形，能搭成504种不同的等腰三角形．‎ ‎26．(12分)如图，在平面直角坐标系中，点A(4，0)，B(0，3)，以线段AB为边在第一象限内作等腰直角三角形ABC，∠BAC＝90°.若第二象限内有一点P，且△ABP的面积与△ABC的面积相等．‎ ‎(第26题)‎ ‎(1)求直线AB的函数表达式．‎ ‎(2)求a的值．‎ ‎(3)在x轴上是否存在一点M，使△MAC为等腰三角形？若存在，直接写出点M的坐标；若不存在，请说明理由．导学号：91354039‎ ‎【解】　(1)设直线AB的函数表达式为y＝kx＋b(k≠0)．由题意，得 解得 ‎∴直线AB的函数表达式为y＝－x＋3.‎ ‎(2)如解图，过点P作PD⊥x轴于点D.‎ 易得BO＝3，AO＝4，‎ ‎∴AB＝＝5.‎ ‎∵△ABC是等腰直角三角形，AB＝AC，‎ ‎∴S△ABC＝.‎ ‎∵点P，且在第二象限，‎ ‎∴PD＝，OD＝－a，‎ ‎∴S△ABP＝S梯形PDOB＋S△AOB－S△APD ‎＝＋×3×4－×(4－a)×＝－a＋5，‎ 14‎ ‎∴－a＋5＝，解得a＝－5.‎ ‎(第26题解)‎ ‎(3)存在．‎ 如解图，分三种情况讨论：‎ ‎①当以点A为顶点时，以点A为圆心，AC长为半径画弧，交x轴于点M1，M2，‎ 易知AM1＝AM2＝AC＝5，‎ ‎∴点M1(－1，0)，M2(9，0)．‎ ‎②当以点C为顶点时，以点C为圆心，AC长为半径画弧，交x轴于点M3，过点C作CE⊥x轴于点E.‎ 易知△AOB≌△CEA≌△CEM3，‎ ‎∴EM3＝AE＝BO＝3，CE＝AO＝4，‎ ‎∴点M3(10，0)．‎ ‎③当以点M为顶点时，作AC的中垂线交x轴于点M4.‎ 易得点C(7，4)，又∵点A(4，0)，‎ ‎∴AC的中点坐标为.‎ 易知AB平行于AC的中垂线，故可设AC中垂线的函数表达式为y＝－x＋b.‎ 由题意，得－×＋b＝2，解得b＝，‎ ‎∴AC中垂线的函数表达式为y＝－x＋.‎ 令y＝0，得x＝，∴点M4.‎ 综上所述，存在点M(－1，0)或(9，0)或(10，0)或，使△MAC为等腰三角形．‎ 14‎ 14‎