2019-2020学年山东省济南市章丘区八年级（上）期末数学试卷 8页

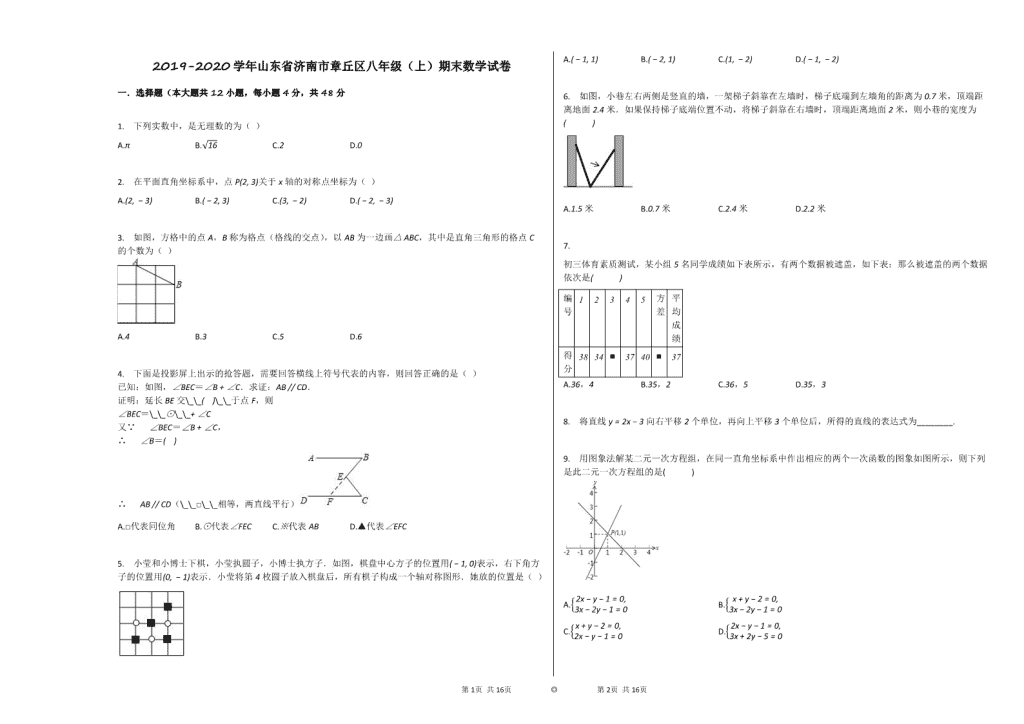
‎2019-2020学年山东省济南市章丘区八年级（上）期末数学试卷 一．选择题（本大题共12小题，每小题4分，共48分 ‎ ‎ ‎1. 下列实数中，是无理数的为（ ） ‎ A.π B.‎16‎ C.‎2‎ D.‎‎0‎ ‎ ‎ ‎2. 在平面直角坐标系中，点P(2, 3)‎关于x轴的对称点坐标为（ ） ‎ A.‎(2, −3)‎ B.‎(−2, 3)‎ C.‎(3, −2)‎ D.‎‎(−2, −3)‎ ‎ ‎ ‎3. 如图，方格中的点A，B称为格点（格线的交点），以AB为一边画‎△ABC，其中是直角三角形的格点C的个数为（ ） ‎ A.‎4‎ B.‎3‎ C.‎5‎ D.‎‎6‎ ‎ ‎ ‎4. 下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容，则回答正确的是（ ） 已知：如图，‎∠BEC＝‎∠B+∠C．求证：AB // CD． 证明：延长BE交__‎(‎    ‎)‎__于点F，则 ‎∠BEC＝__‎⊙‎__‎+∠C 又∵ ‎∠BEC＝‎∠B+∠C， ∴ ‎∠B＝‎(‎    ‎)‎ ∴ AB // CD（__□__相等，两直线平行） ‎ A.□代表同位角 B.‎⊙‎代表‎∠FEC C.‎※‎代表AB D.▲代表‎∠EFC ‎ ‎ ‎5. 小莹和小博士下棋，小莹执圆子，小博士执方子．如图，棋盘中心方子的位置用‎(−1, 0)‎表示，右下角方子的位置用‎(0, −1)‎表示．小莹将第‎4‎枚圆子放入棋盘后，所有棋子构成一个轴对称图形．她放的位置是（ ） ‎ A.‎(−1, 1)‎ B.‎(−2, 1)‎ C.‎(1, −2)‎ D.‎‎(−1, −2)‎ ‎ ‎ ‎6. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为‎0.7‎米，顶端距离地面‎2.4‎米．如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面‎2‎米，则小巷的宽度为‎(‎        ‎)‎ ‎ A.‎1.5‎米 B.‎0.7‎米 C.‎2.4‎米 D.‎2.2‎米 ‎ ‎ ‎7. ‎ 初三体育素质测试，某小组‎5‎名同学成绩如下表所示，有两个数据被遮盖，如下表：那么被遮盖的两个数据依次是‎(‎        ‎‎)‎ 编号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 方差 平均成绩 得分 ‎38‎ ‎34‎ ‎■‎ ‎37‎ ‎40‎ ‎■‎ ‎37‎ A.‎36‎，‎4‎ B.‎35‎，‎2‎ C.‎36‎，‎5‎ D.‎35‎，‎‎3‎ ‎ ‎ ‎8. 将直线y=2x−3‎向右平移‎2‎个单位，再向上平移‎3‎个单位后，所得的直线的表达式为________. ‎ ‎ ‎ ‎9. 用图象法解某二元一次方程组，在同一直角坐标系中作出相应的两个一次函数的图象如图所示，则下列是此二元一次方程组的是(        )   ‎ A.‎2x−y−1=0,‎‎3x−2y−1=0‎ B.x+y−2=0,‎‎3x−2y−1=0‎ C.x+y−2=0,‎‎2x−y−1=0‎ D.‎2x−y−1=0,‎‎3x+2y−5=0‎ ‎ ‎ ‎ 第13页 共16页 ◎ 第14页 共16页 ‎10. 如图，在Rt△ABC中，‎∠ACB=‎‎90‎‎∘‎，AB=4‎．分别以AC，BC为直径作半圆，面积分别记为S‎1‎，S‎2‎，则S‎1‎‎+‎S‎2‎的值等于‎(‎         ‎)‎ ‎ A.‎3π B.‎2π C.‎8π D.‎‎4π ‎ ‎ ‎11. 如图，在平面直角坐标系中，点A(−1, 0)‎，B(0, 3)‎，直线BC交坐标轴于B、C，且‎∠CBA＝‎45‎‎∘‎，点M在直线BC上，且AM⊥AB，则直线BC的解析式为（ ） ‎ A.y=‎2‎‎3‎x+3‎ B.y＝x+3‎ C.y=‎1‎‎3‎x+3‎ D.‎y=‎1‎‎2‎x+3‎ ‎ ‎ ‎12. 甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．则下列结论： ①A，B两城相距‎300‎千米； ②乙车比甲车晚出发‎1‎小时，却早到‎1‎小时； ③乙车出发后‎1.5‎小时追上甲车；  ④当甲、乙两车相距‎50‎千米时，t=‎‎5‎‎4‎或‎15‎‎4‎． 其中正确的结论有(        ) ‎ A.‎2‎个 B.‎1‎个 C.‎3‎个 D.‎4‎个 二．填空题（本大题共6小题，每小题4分，共24分）‎ ‎ ‎ ‎ 若x+3‎是‎4‎的算术平方根，则x＝________；若‎−27‎的立方根是y−1‎，则y＝________． ‎ ‎ ‎ ‎ 若‎|x+y+1|‎与‎(x−y−2‎‎)‎‎2‎互为相反数，则‎(2x−4y‎)‎‎2‎＝________． ‎ ‎ ‎ ‎ 如图，‎∠1‎＝‎120‎‎∘‎，‎∠2‎＝‎60‎‎∘‎，‎∠3‎＝‎100‎‎∘‎，则‎∠4‎＝________时，AB // EF． ‎ ‎ ‎ ‎ 已知A、B的坐标为‎(−2, 0)‎，‎(4, 0)‎，点P在直线y=‎1‎‎2‎x+2‎上，若‎△ABP为等腰三角形，则这样的P点共有________个． ‎ ‎ ‎ ‎ 若直线y＝kx与四条直线x＝‎1‎，x＝‎2‎，y＝‎1‎，y＝‎2‎围成的正方形有公共点，则k的取值范围是________． ‎ ‎ ‎ ‎ 如图，在平面直角坐标系中，函数y＝‎2x和y＝‎−x的图象分别为直线l‎1‎、l‎2‎，过点‎(1, 0)‎作x轴的垂线交l‎1‎于点A‎1‎，过点A‎1‎作y轴的垂线交l‎2‎于点A‎2‎，过点A‎2‎作x轴的垂线交l‎1‎于点A‎3‎，过点A‎3‎作y轴的垂线交l‎2‎于点A‎4‎，…，依次进行下去，则点A‎2021‎的坐标为________． ‎ 三．解答题（本大题共9小题，共78分．解答应写出文字说明、证明过程或演算步票）‎ ‎ ‎ ‎ 计算： ‎ ‎（1）‎‎27‎‎−‎‎12‎‎3‎ 第13页 共16页 ◎ 第14页 共16页 ‎ ‎ ‎（2）‎‎32‎‎−3‎1‎‎2‎+‎‎2‎ ‎ ‎ ‎ 解方程组： ‎ ‎（1）x−y=4‎‎3x+y=16‎‎ ‎；‎ ‎ ‎ ‎（2）x‎2‎‎−y−1‎‎3‎=1‎‎3x+2y=10‎‎ ‎．‎ ‎ ‎ ‎ ‎ ‎（1）画出‎△ABC关于y轴对称的‎△A′B′C′‎（其中A′‎、B′‎、C′‎分别为A、B、C的对应点）；‎ ‎ ‎ ‎（2）直接写出A′‎、B′‎、C′‎三点的坐标；‎ ‎ ‎ ‎（3）在y轴上找一点P使得PA+PB最小，画出点P所在的位置（保留作图痕迹，不写作法），并求出PA+PB的最小值．‎ ‎ ‎ ‎ 如图，四边形ABCD中，‎∠C＝‎90‎‎∘‎，BD平分‎∠ABC，AD＝‎3‎，E为AB上一点，AE＝‎4‎，ED＝‎3‎，求CD的长． ‎ ‎ ‎ ‎ 某高校共有‎5‎个大餐厅和‎2‎个小餐厅．经过测试：同时开放‎1‎个大餐厅、‎2‎个小餐厅，可供‎1680‎名学生就餐；同时开放‎2‎个大餐厅、‎1‎个小餐厅，可供‎2280‎名学生就餐． ‎ ‎（1）求‎1‎个大餐厅、‎1‎个小餐厅分别可供多少名学生就餐；‎ ‎ ‎ ‎（2）若‎7‎个餐厅同时开放，能否供全校的‎5300‎名学生就餐？请说明理由．‎ ‎ ‎ ‎ 某校开展了以“不忘初心，奋斗新时代”为主题的读书活动．校德育处对本校八年级学生九月份“阅读该主题相关书籍的读书量”（下面简称：“读书量”）进行了随机抽样调查，并对所有随机抽取学生的“读书量”（单位：本）进行了统计，如图所示： 根据以上信息，解答下列问题： ‎ ‎（1）补全上面两幅统计图，填出本次所抽取学生九月份“读书量”的众数为________；‎ ‎ ‎ ‎（2）求本次所抽取学生九月份“读书量”的平均数；‎ ‎ ‎ ‎（3）已知该校八年级有‎1200‎名学生，请你估计该校八年级学生中，九月份“读书量”为‎5‎本的学生人数．‎ ‎ ‎ ‎ 如图，等腰三角形ABC中，AB＝AC＝‎5cm，BC＝‎6cm，动点P从点A出发，沿路线A→B→C匀速运动，速度为‎1cm/‎秒，运动到C点停止，设运动时间为t(s)‎，‎△APC的面积为y(cm‎2‎)‎． ‎ ‎（1）求‎△ABC的面积；‎ ‎ ‎ ‎（2）求等腰‎△ABC腰上的高；‎ ‎ ‎ 第13页 共16页 ◎ 第14页 共16页 ‎（3）是否存在某一时刻t，使得‎△APC的面积正好是‎△ABC面积的‎5‎‎12‎，若存在，求出t的值；若不存在，说明理由．‎ ‎ ‎ ‎ 如图‎1‎，直线MN与直线AB、CD分别交于点E、F，‎∠1‎与‎∠2‎互补． ‎ ‎（1）试判断直线AB与直线CD的位置关系，并说明理由；‎ ‎ ‎ ‎（2）如图‎2‎，‎∠BEF与‎∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF // GH；‎ ‎ ‎ ‎（3）如图‎3‎，在（2）的条件下，连接PH，K是GH上一点使‎∠PHK＝‎∠HPK，作PQ平分‎∠EPK，求‎∠HPQ的度数．‎ ‎ ‎ ‎ 在平面直角坐标系中，一次函数y=‎1‎‎2‎x+2‎的图象交x轴、y轴分别于A、B两点，与直线OC相交于第二象限，交点为点C，且C点纵坐标为l． ‎ ‎（1）求点A、点B的坐标；‎ ‎ ‎ ‎（2）若点D为直线y=‎1‎‎2‎x+2‎上一点，且点D在第一象限，若‎△OCD的面积与‎△ABO的面积相等，求直线OC与直线OD的函数关系式；‎ ‎ ‎ ‎（3）在（2）的条件下，点P为线段CD上一点，过点P作y轴的平行线，与直线OD、直线OC分别相交于点E、点F，若PE＝‎2EF，求点P的坐标．‎ 第13页 共16页 ◎ 第14页 共16页 参考答案与试题解析 ‎2019-2020学年山东省济南市章丘区八年级（上）期末数学试卷 一．选择题（本大题共12小题，每小题4分，共48分 ‎1.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 算三平最根 无理较的识轻 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎2.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 关于较洗、y装对氢的点的坐标 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎3.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 勾股定体的展定理 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎4.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 同位来、内德圆、同终内角 平行水因判定 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎5.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 坐标与图表镜化-对称 位因顿确定 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎6.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 勾股表理抛应用 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎7.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 方差 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎8.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 一正间仅图宽与几何变换 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎9.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 一次于数与旋恒一次普程（组）‎ 待定正数键求一程植数解析式 ‎【解析】‎ 第13页 共16页 ◎ 第14页 共16页 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎10.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 勾体定展 勾股定理较综脱与创新 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎11.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 勾体定展 一次常数图按上点入适标特点 待定正数键求一程植数解析式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎12.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 函表的透象 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 二．填空题（本大题共6小题，每小题4分，共24分）‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 算三平最根 立方于的性术 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 二元一都接程组的解 非负数的较质：绝对值 非负射的纳质：算术棱方础 加减正元东树说元一次方程组 代入使碳古解革元一次方程组 非负数的常树：偶次方 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 平行线明判轮与性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 等腰三验库的性质 一次常数图按上点入适标特点 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 一次水体的性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 规律型：三形的要化类 一次常数图按上点入适标特点 正比例来数的斗象 第13页 共16页 ◎ 第14页 共16页 规律型：因字斯变化类 规律型：点的坐较 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 三．解答题（本大题共9小题，共78分．解答应写出文字说明、证明过程或演算步票）‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 分于落理化 二次根明的织合运算 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 代入使碳古解革元一次方程组 二元一都接程组的解 加减正元东树说元一次方程组 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 轴明称月去最键路线问题 作图-射对称变面 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 角平较线的停质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 二元一水使程组种应用—鉴其他问题 二元一因方程似应用 二元一正构程组的置用——移程问题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 扇表统病图 条都连计图 加水正均数 众数 用样射子计总体 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 三角使如合题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 平行线明判轮与性质 余因顿补角 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 两直正键行问题 两直正区直问题 第13页 共16页 ◎ 第14页 共16页 两直线相来非垂筒问题 相交线 待定正数键求一程植数解析式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 第13页 共16页 ◎ 第14页 共16页