2020春八年级数学下册第18章函数及其图象18-2函数的图象1平面直角坐标系习题课件华东师大版 34页

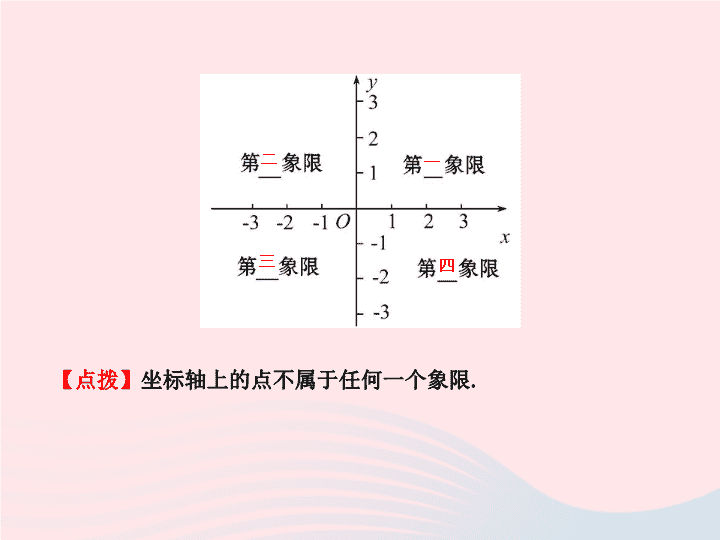
1. 平面直角坐标系 1. 平面直角坐标系 (1) 平面直角坐标系是由平面上两条 _____ 重合、互相 _____ 且具 有相同 _________ 的数轴组成的 . 通常把其中水平的一条数轴叫做 __ 轴或横轴 , 取向右为 ___ 方向；铅直的数轴叫做 __ 轴或纵轴，取 向上为 ___ 方向；两数轴的交点 O 叫做 _________. (2) 在直角坐标系中，两条坐标轴把平面分成四个区域，分别称 为第一、二、三、四象限，如图 . 原点 垂直 单位长度 x 正 y 正 坐标原点 【 点拨 】 坐标轴上的点不属于任何一个象限 . 一 二 三 四 2. 平面内点的坐标 (1) 点的坐标的表示方法 _______ 在前， _______ 在后，中间用逗号隔开，用 _____ 括起来 . (2) 各象限内及坐标轴上点的坐标的特征 . 设 P(x,y), ① 若点 P 在第一象限，则 __________ ； ②若点 P 在第二象限，则 ________ ； 横坐标 纵坐标 括号 x ＞ 0,y ＞ 0 x<0,y>0 ③ 若点 P 在第三象限，则 ________ ； ④若点 P 在第四象限 , 则 ________ ； ⑤若点 P 在 x 轴上，则 ____ ； ⑥若点 P 在 y 轴上，则 ____ ； ⑦若点 P 在坐标原点，则 ________. (3) 对称点的坐标 ①点 P(x,y) 关于 x 轴的对称点 P 1 _______ ； ②点 P(x,y) 关于 y 轴的对称点 P 2 _______ ； ③点 P(x,y) 关于原点的对称点 P 3 ________. x<0,y<0 x>0,y<0 y=0 x=0 x=0,y=0 (x,-y) (-x,y) (-x,-y) 【 预习思考 】 1. 平面直角坐标系中 , 点 (0,2),(2,0) 的位置相同吗 ? 为什么 ? 提示： 不同 . 理由 : 点 (0,2) 在 y 轴上 , 点 (2,0) 在 x 轴上 , 一个点的坐标是一个有序实数对 . 2. 平面直角坐标系中点与坐标存在什么联系 ? 提示： 由点的位置可求其坐标；由坐标可找到点所在的位置，平面直角坐标系中的点和有序实数对是一一对应的 . 平面直角坐标系中点的特征及应用 【 例 1】(1)(2012· 扬州中考 ) 在平面直角坐标系中，点 P(m ， m － 2) 在第一象限内，则 m 的取值范围是 __________. (2) 如图是永州市几个主要景点示意图 , 根据图中信息可确定九嶷山的中心位置 C 点的坐标为 __________. 【 解题探究 】 (1)① 第一象限内点的特征 : 横坐标的符号为 正 , 纵坐标的符号为 正 ； ②点 P(m,m-2) 在第一象限 , 所以 解不等式组得 m>2 . 故 m 的取值范围是 m >2 . (2)① 由图可知 :A 点坐标为 (1,0) ,B 点坐标为 (0,1) , 本题坐标系 是以点 A 所在的水平直线为 x 轴 , 且向 右 为正方向 , 点 B 所在的竖直 直线为 y 轴 , 且向 上 为正方向 , 这两直线的 交点 为坐标原点； ②根据①的探究 , 所以 C 点坐标为 (3,1) . 【 规律总结 】 平面直角坐标系中点的坐标规律 点的坐标符号 (+,+) ⇔ 第一象限； 点的坐标符号 (-,+) ⇔ 第二象限； 点的坐标符号 (-,-) ⇔ 第三象限； 点的坐标符号 (+,-) ⇔ 第四象限； 点的坐标符号 (±,0) ⇔ 在 x 轴上； 点的坐标符号 (0,±) ⇔ 在 y 轴上； 点的坐标符号 (0,0) ⇔ 与坐标原点重合 . 【 跟踪训练 】 1. 在平面直角坐标系中 , 下面的点在第一象限的是 ( ) (A)(1,2) (B)(-2,3) (C)(0,0) (D)(-3,-2) 【 解析 】 选 A. 因为第一象限的条件是 : 横坐标是正数 , 纵坐标也是正数 , 而各选项中符合纵坐标为正 , 横坐标也为正的只有 A(1,2). 2.(2012· 菏泽中考 ) 点 (-2,1) 所在的象限是 ( ) (A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限 【 解析 】 选 B. 点 (-2,1) 的横坐标为负 , 纵坐标为正 , 所以点 (-2,1) 在第二象限 . 3. 在平面直角坐标系中 , 若点 P(a,b) 在第二象限 , 则点 Q(1-a,-b) 所在的象限是 ( ) (A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限 【 解析 】 选 D.∵ 点 P(a,b) 在第二象限 ,∴a ＜ 0,b ＞ 0 ； ∴ -a ＞ 0,-b ＜ 0, 则 1-a ＞ 0, 即点 Q(1-a,-b) 在第四象限 . 【 变式备选 】 若点 在第四象限 , 则 m 的取值范围是 ( ) (A) (B) (C) (D) 【 解析 】 选 C.∵ 点 在第四象限 . 解得 4.(2012· 南安中考 ) 如图 , 已知棋子“车”的坐标为 (-2,3), 棋子“马”的坐标为 (1,3), 则棋子“炮”的坐标为 ( ) (A)(3,2) (B)(3,1) (C)(2,2) (D)(-2,2) 【 解析 】 选 A. 棋子 “ 车 ” 的坐标为 (-2,3), 棋子 “ 马 ” 的坐标为 (1,3), 纵坐标都是 3, 所以棋子 “ 炮 ” 的纵坐标为 2 ；根据 “ 车 ” 和 “ 马 ” 的横坐标 -2,1, 确定棋子 “ 炮 ” 的横坐标为 3. 所以 “ 炮 ” 的坐标为 (3,2). 5.(1) 在直角坐标系中 , 描出下列各点： A(4,3),B(-2,3), C(-4,-1),D(2,-2). (2) 写出图中 E ， F ， G ， H ， O 各点的坐标 , 你能从中得出什么结论？ 【 解析 】 (1) (2)E(5,0),F(0,-4),G(-1,0),H(0,2),O(0,0). 结论： x 轴上的点的纵坐标为零 ,y 轴上的点的横坐标为零 . 平面直角坐标系中点的对称 【 例 2】(10 分 ) 如图 , 请写出平面直角坐标系中“鱼”上所标各点 A ， B ， C ， D ， E 的坐标 , 并回答下列问题 : (1) 点 A ，点 B 和点 E, 点 C 与点 D 的位置有什么特点 ? (2) 从点 B 与点 E, 点 C 与点 D 的位置看 , 它们的坐标有什么特点 ? (3) 总结 (1)(2), 你能得到什么结论 ? 【 规范解答 】 由平面直角坐标系中点的位置可得 , A (-2,0) ,B (0,-2) ,C (2,-1) ,D (2,1) , E(0,2) . ………………………… 4 分 易错提醒 : 对称点的坐标规律：关于 x 轴对称的点，横坐标不变，纵坐标变为相反数 . (1)∵ 点 A 的纵坐标为 0 , 点 B 和点 E 的横坐标为 0 , 点 C 和点 D 的横坐标都是 2 ,∴ 点 A 在 x 轴上 , 点 B 和点 E 在 y 轴上 , 且点 B 和点 E 、点 C 与点 D 都关于 x 轴对称 . …………………………………………… 6 分 (2) 点 B 与点 E 、点 C 与点 D, 它们的横坐标 相同 , 纵坐标 互为相反数 . ……………………………………………………………… 8 分 (3) 关于 x 轴对称的点的横坐标 相同 , 纵坐标 互为相反数 . ………………………………………………………………… 10 分 【 互动探究 】 点 P 关于 x 轴、 y 轴的对称点分别为 P 1 和 P 2 . 则点 P 1 ， P 2 有什么关系？ 提示： 关于原点对称 . 【 规律总结 】 对称点的坐标规律 (1) 关于 x 轴对称的点 , 横坐标相同 , 纵坐标互为相反数； (2) 关于 y 轴对称的点 , 纵坐标相同 , 横坐标互为相反数； (3) 关于原点对称的点 , 横坐标与纵坐标都互为相反数 . 【 跟踪训练 】 6.(2012· 绵阳中考 ) 点 M(1,-2) 关于原点对称的点的坐标是 ( ) (A)(-1,-2) (B)(1,2) (C)(-1,2) (D)(-2,1) 【 解析 】 选 C. 若两个点关于原点对称，则这两个点的横、纵坐标均互为相反数 ,∴ 点 (1,-2) 关于原点对称的点的坐标为 (-1,2). 故选 C. 7. 如果点 P(4,-5) 和点 Q(a,b) 关于原点对称 , 则 a+b 的值为 ___________. 【 解析 】 ∵ 点 P(4,-5) 和点 Q(a,b) 关于原点对称 ,∴a ＝ -4, b ＝ 5,∴a+b=5-4=1. 答案： 1 8. 在平面直角坐标系中 ,△ABC 的三个顶点的位置如图所示 , 点 A′ 的坐标是 (-2,2), 现将△ ABC 平移 , 使点 A 变换为点 A′, 点 B′ ， C′ 分别是 B ， C 的对应点 . (1) 请画出平移后的像△ A′B′C′( 不写画法 ), 并直接写出点 B′ ， C′ 的坐标 :B′___________ 、 C′__________ ； (2) 若△ ABC 内部一点 P 的坐标为 (a,b), 则点 P 的对应点 P′ 的坐标是 __________. 【 解析 】 (1) 如图 :△A′B′C′ 就是所求作的三角形 . B′(-4,1),C′(-1,-1) ； (2) 根据平移的规律 ,A 到 A′ 的变化规律是向左平移 5 个单位长度 , 向下平移 2 个单位长度 . 即如 A(x,y), 可求 A′ 的坐标是 (x-5,y-2). 故 P′ 的坐标是 (a-5,b-2). 1. 已知点 A 的坐标是 (a,b), 若 a+b ＜ 0 ， ab ＞ 0. 则点 A 在第 __________ 象限 .( ) (A) 一 (B) 二 (C) 三 (D) 四 【 解析 】 选 C. 由 a+b ＜ 0 ， ab ＞ 0 可知 ,a ， b 均为负数 . 2.(2012· 成都中考 ) 如图 , 在平面直角坐标系 xOy 中 , 点 P(-3,5) 关于 y 轴的对称点的坐标为 ( ) (A)(-3,-5) (B)(3,5) (C)(3,-5) (D)(5,-3) 【 解析 】 选 B. 根据关于 y 轴对称的点的坐标特征 , 横坐标互为相反数 , 纵坐标相等 ,∴ 点 P(-3,5) 关于 y 轴的对称点的坐标为 (3,5). 3.(2012· 安顺中考 ) 以方程组 的解为坐标的点 (x,y) 在第 __________ 象限 . 【 解析 】 解方程组得 所以 在第一象限 . 答案： 一 4. 在平面直角坐标系中 , 若点 M(1,3) 与点 N(x,3) 之间的距离是 5, 则 x 的值是 ___________ ；若 H 点与 N 点关于 y 轴对称 , 则 H 点的坐标是 ___________. 【 解析 】 ∵ 点 M(1,3) 与点 N(x,3) 的纵坐标相同 , 点 M(1,3) 与点 N(x,3) 之间的距离是 5,∴|x-1|=5, 解得 x=-4 或 6, 即 N 点的坐标为 (-4,3) 或 (6,3), 又 H 点与 N 点关于 y 轴对称 ,∴H 点的坐标是 (4,3) 或 (-6,3). 答案： -4 或 6 (4,3) 或 (-6,3) 5. 常用的确定物体位置的方法有两种 . 如图 , 在 4×4 个边长为 1 的正方形组成 的方格中 , 标有 A,B 两点 . 请你用两种 不同方法表述点 B 相对点 A 的位置 . 【 解析 】 方法一：用有序实数对 (a,b) 表示 .( 答案不唯一 ) 比 如：以点 A 为原点 , 水平方向为 x 轴 , 建立直角坐标系 , 则 B(3,3). 方法二：用方向和距离表示 . 比如 : B 点位于 A 点的东北方向 ( 北 偏东 45° 等均可 ), 距离Ａ点 处 .