八年级下册数学同步练习第2章复习1 湘教版 8页

‎《四边形》复习 一．选择题（共8小题）‎ ‎1．已知一个多边形的内角和等于它的外角和，则这个多边形的边数为（　　）‎ A．3 B．4 C．5 D．6‎ ‎　‎ ‎2．下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎　‎ ‎3．如图，在▱ABCD中，BM是∠ABC的平分线交CD于点M，且MC=2，▱ABCD的周长是14，则DM等于（　　）[来源:学*科*网]‎ A．1 B．2 C．3 D．4‎ 第5题图 第4题图 第3题图 ‎　‎ ‎4．如图，△ABC的中线BD、CE交于点O，连接OA，点G、F分别为OC、OB的中点，BC=8，AO=6，则四边形DEFG的周长为（　　）‎ A．12 B．14 C．16 D．18‎ ‎　‎ ‎5．如图，在△ABC中，AB=6，AC=8，BC=10，P为边BC上一动点（且点P不与点B、C重合），PE⊥AB于E，PF⊥AC于F，M为EF中点．设AM的长为x，则x的取值范围是（　　）‎ A．4≥x＞2.4 B．4≥x≥2.4 C．4＞x＞2.4 D．4＞x≥2.4‎ ‎　‎ ‎6．顺次连接四边形四条边的中点，所得的四边形是菱形，则原四边形一定是（　　）‎ A．平行四边形 B．对角线相等的四边形 C．矩形 D．对角线互相垂直的四边 ‎　‎ ‎7．如图，以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE，使AD=DE=CE，∠DEC=90°，且点E在平行四边形内部，连接AE、BE，则∠AEB的度数是（　　）‎ A．120° B．135° C．150° D．45°‎ ‎　[来源:学_科_网Z_X_X_K]‎ 第8题图 第7题图 ‎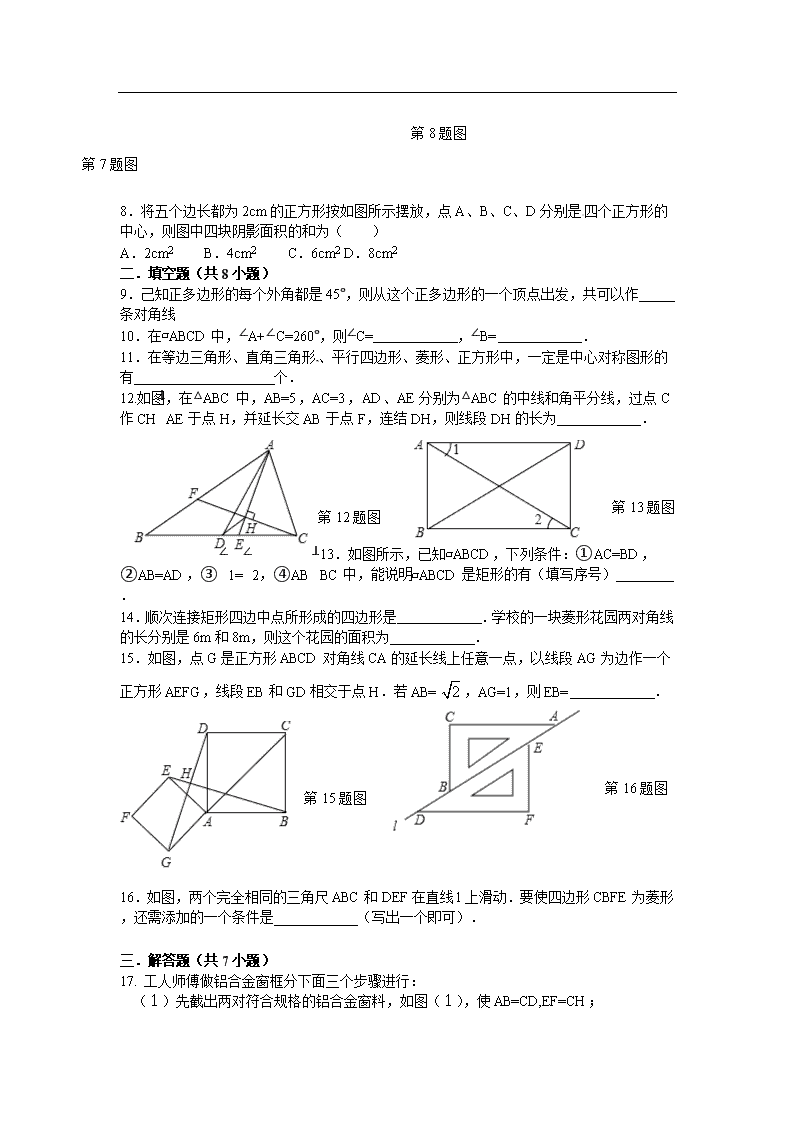8．将五个边长都为2cm的正方形按如图所示摆放，点A、B、C、D分别是四个正方形的中心，则图中四块阴影面积的和为（　　）‎ A．2cm2 B．4cm2 C．6cm2 D．8cm2‎ 二．填空题（共8小题）‎ ‎9．己知正多边形的每个外角都是45°，则从这个正多边形的一个顶点出发，共可以作　　　　　　条对角线 ‎10．在▱ABCD中，∠A+∠C=260°，则∠C=　　　　　　，∠B=　　　　　　．‎ ‎11．在等边三角形、直角三角形、平行四边形、菱形、正方形中，一定是中心对称图形的有　　　　　　________个．‎ ‎12.如图，在△ABC中，AB=5，AC=3，AD、AE分别为△ABC的中线和角平分线，过点C作CH⊥AE于点H，并延长交AB于点F，连结DH，则线段DH的长为　　　　　　．‎ ‎　‎ 第12题图 第13题图 ‎13．如图所示，已知▱ABCD，下列条件：①AC=BD，②AB=AD，③∠1=∠2，④AB⊥BC中，能说明▱ABCD是矩形的有（填写序号）　　　　　　．‎ ‎14．顺次连接矩形四边中点所形成的四边形是　　　　　　．学校的一块菱形花园两对角线的长分别是6m和8m，则这个花园的面积为　　　　　　．‎ ‎15．如图，点G是正方形ABCD对角线CA的延长线上任意一点，以线段AG为边作一个正方形AEFG，线段EB和GD相交于点H．若AB=，AG=1，则EB=　　　　　　．‎ ‎　‎ ‎[来源:Z|xx|k.Com]‎ 第16题图 第15题图 ‎16．如图，两个完全相同的三角尺ABC和DEF在直线l上滑动．要使四边形CBFE为菱形，还需添加的一个条件是　　　　　　（写出一个即可）．‎ ‎　‎ 三．解答题（共7小题）‎ ‎17. 工人师傅做铝合金窗框分下面三个步骤进行：‎ ‎　（１）先截出两对符合规格的铝合金窗料，如图（１），使AB=CD,EF=CH；‎ ‎　（２）摆成如图（２）的四边形，则这时窗框的形状是 形，根据的数学道理是 ；‎ ‎　（３）将直角尺靠紧窗框的一个角，如图（３），调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时，如图（４），说明窗框合格，这时窗框是 形，根据的数学道理是 .‎ ‎18. 已知□的周长为40cm，∶∶，求和的长.‎ A B ‎ C ‎ O ‎ D ‎ 第19题图 ‎ ‎19. 如图，四边形ABCD是平行四边形AD=12、AB=13，BD⊥AD，求OB的长及平行四边形ABCD的面积．‎ ‎[来源:Z&xx&k.Com]‎ ‎20. 已知：如图，四边形是菱形，过的中点作的垂线，交于点，交的延长线于点．‎ ‎（1）求证：.‎ 第20题图 ‎ A B ‎ E ‎ D ‎ C ‎ F ‎ M ‎ ‎（2）若，求菱形的周长．‎ ‎21. 如图，△ABC中∠ACB＝90o，点D、E分别是AC，AB的中点，点F在BC的延长线上，且∠CDF＝∠A。求证：四边形DECF是平行四边形。‎ A B D C F E ‎22.如图，在矩形AB CD中，AB=12cm，BC=6cm，点P沿AB边从点A开始向点B以2cm/秒的速度移动；点Q沿DA边从点D开始向点A以1cm/秒的速度移动，如果P、Q同时出发，用t(秒）表示移动的时间（0＜t＜6）.‎ ‎(1)当t为何值时，△QAP为等腰直角三角形？‎ ‎(2)四边形QAPC的面积与t的大小有关系吗?请说明理由. ‎ ‎　　‎ ‎[来源:学。科。网Z。X。X。K]‎ ‎23.问题背景 ‎ 甲、乙、丙三名同学探索课本上一道题：如图1，E是边长为a的正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形．‎ 任务要求：‎ ‎（1）请你在图1中画出旋转后的图形 甲、乙、丙三名同学又继续探索：‎ 在正方形ABCD中，∠EAF=45°，点F为BC上一点，点E为DC上一点，∠EAF的两边AE、AF分别与直线BD交于点M、N．连接EF 甲发现：线段BF，EF，DE之间存在着关系式EF=BF+DE；‎ 乙发现：△CEF的周长是一个恒定不变的值；‎ 丙发现：线段BN，MN，DM之间存在着关系式 ‎（2）现请你参与三位同学的研究工作中来，你认为三名同学中哪个的发现是正确的，并说明你的理由．‎ 参考答案：‎ ‎　‎ 一．选择题（共8小题）‎ ‎1．B； 2．B； 3．C； 4．B； 5．D； 6．B； 7．B； 8．B；‎ ‎　‎ 二．填空题（共8小题）‎ ‎9．5； 10．130°； 50°； 11．3； 12．1； 13．①④； 14．菱形24m2； ‎ ‎15．； 16．答案不惟一，如：CB=BF；BE⊥CF；∠EBF=60°；BD=BF等； ‎ 三．解答题（共7小题）‎ ‎17. 平行四边形 两组对边相等的四边形是平行四边形 ‎ 矩形 有一个角是直角的平行四边形是矩形 ‎18. ㎝， ㎝ ‎19.OB=2.5 S=60‎ ‎20.略 （2）16‎ ‎21.略 ‎22. 解: ‎ ‎(1)∵当QA=AP时,△QAP为等腰直角三角形.‎ ‎∴‎ ‎，‎ 即t为2秒时，△QAP为等腰直角三角形.‎ ‎(2)四边形QAPC的面积=为常数.‎ 所以四边形QAPC的面积与t的大小没有关系.‎ ‎23. 解：（1）画图如图1所示；‎ ‎（2）甲、乙、丙三名同学的发现都是正确的；‎ ‎①甲发现正确；理由如下：‎ 如图2所示，‎ 延长CB到K，使BK=DE，连AK，‎ ‎∵四边形ABCD是正方形，‎ ‎∴AB=AD，∠ABF=∠ABK=∠ADE=90°，‎ 在△AKB和△AED中，‎ AD＝AB ‎∠ABK＝∠ADE BK＝DE ‎∴△AKB≌△AED（SAS），‎ ‎∴∠BAK=∠DAE，‎ ‎∵∠BAF+∠DAE=45°，‎ ‎∴∠BAF+∠BAK=45°，‎ 即∠KAF=45°，‎ ‎∴∠KAF=∠FAE，‎ 在△AKF和△AEF中，‎ AK＝AE ‎∠KAF＝∠FAE AF＝AF ‎∴△AKF≌△AEF（SAS），‎ ‎∴KF=EF，‎ 又∵BK=DE，‎ ‎∴EF=BF+DE；‎ ‎②乙发现正确；理由如下：‎ 延长CB到K，使BK=DE，连接AK，如图2所示：‎ 同①得：△AKB≌△AED，‎ ‎∴∠BAK=∠DAE，‎ ‎∵∠BAF+∠DAE=45°，‎ ‎∴∠BAF+∠BAK=45°，‎ 即∠KAF=45°，‎ ‎∴∠KAF=∠FAE，‎ 在△AKF和△AEF中，‎ AK＝AE ‎∠KAF＝∠FAE AF＝AF ‎∴△AKF≌△AEF（SAS），‎ ‎∴KF=EF，‎ 又∵BK=DE，‎ ‎∴EF=BF+DE；‎ ‎△CEF周长=CF+CE+EF ‎=CF+CE+（BF+DE）‎ ‎=（CF+BF）+（CE+DE）‎ ‎=BC+DC=2a（定值）；‎ ‎③丙发现正确；理由如下：‎ 如图3，在AK上截取AG=AM，连接BG，GN，‎ 在△ABG和△ADM中，‎ AG＝AM ‎∠KAB＝∠EAD AB＝AD ‎∴△ABG≌△ADM（SAS），‎ ‎∴BG=DM，∠ABG=∠ADB=45°，‎ 又∵∠ABD=45°，‎ ‎∴∠GBD=90°，‎ ‎∵∠BAF+∠DAE=45°，‎ ‎∴∠KAF=45°，‎ ‎∴∠KAF=∠FAE，‎ 在△GAN和△NAM中，‎ AG＝AM ‎∠KAF＝∠FAE AN＝AN ‎∴△GAN≌△NAM（SAS），‎ ‎∴NG=MN，‎ ‎∵∠GBD=90°，‎ ‎∴BG2+BN2=NG2，‎ ‎∴BN2+DM2=MN2；‎ 综上所述：甲、乙、丙三名同学的发现都是正确的．‎ ‎ ‎