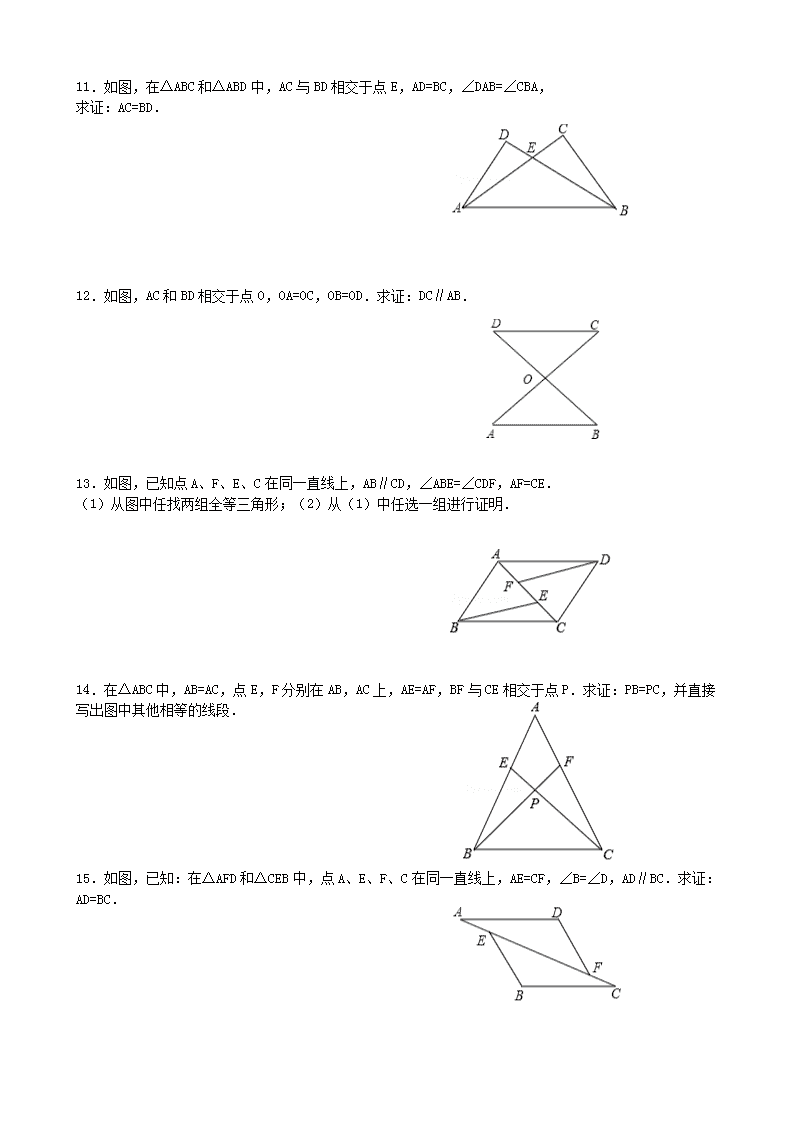苏科版八年级数学上寒假作业（苏教版八年级上册数学寒假作业共8份） 28页

第 6 题图 图2 A B F D E C 第 7 题图 第 8 题图 第 9 题图 苏教版八年级上册数学寒假作业 初二数学寒假作业（8 份） 1（全等三角形） 一、填空与选择 1．已知△ABC≌△DEF，∠A=80°，∠E=50°，则∠F 的度数为（ ） A、 30° B、 50° C、 80° D、 100° 2．已知图中的两个三角形全等，则  的度数是（ ） A．72° B．60° C．58° D．50° 3．如图，∠E=∠F=90°，∠B=∠C，AE=AF，给出下列结论：①∠1=∠2；②BE=CF；③△ACN≌△ABM；④CD=DN， 其中正确的结论有（ ） A、1 个 B、2 个 C、3 个 D、4 个 4．△ABC 是格点三角形（顶点在网格线的交点），则在图中能够作出△ABC 全等且有一条公共边的格点三角 形（不含△ABC）的个数是（ ） A、1 个 B、2 个 C、3 个 D、4 个 5．如图，AC、BD 相交于点 0，∠A=∠D，请补充一个条件，使△AOB≌△DOC，你补充的条件是 （填 出一个即可）． 6．已知，如图：∠ABC =∠DEF，AB =DE，要说明△ABC ≌△DEF： 1）若以“SAS”为依据，还要添加的条件为______________； 2）若以“ASA”为依据，还要添加的条件为______________； 3）若以“AAS”为依据，还要添加的条件为______________． 7．如图∠ACB＝∠DFE，BC＝EF，根据“ASA”,应补充一个直接条件___________，根据“AAS”，那么补 充的条件为____________，才能使△ABC≌△DEF． 8．如图，在 Rt△ABC 中，∠C=90°，AC=10，BC=5，线段 PQ=AB，P、Q 两点分别在 AC 和过点 A 且垂直于 AC 的射线 AO 上运动，当 AP= 时，△ABC 和△PQA 全等. 9．如右图示，△ABE 和△ADC 是△ABC 分别沿着 AB，AC 边翻折 180°形成的，若∠1∶∠2∶∠3=28∶5∶3， 则∠α的度数为 。 10．AD 是△ABC 的边 BC 上的中线，AB＝12，AC＝8，则中线 AD 的取值范围是 二、简答题 第 5 题图 B A C 第 4 题图第 3 题图 A F B C D M E N 1 2 a c ca b  50° 58° 72° 第 2 题图 11．如图，在△ABC 和△ABD 中，AC 与 BD 相交于点 E，AD=BC，∠DAB=∠CBA， 求证：AC=BD． 12．如图，AC 和 BD 相交于点 O，OA=OC，OB=OD．求证：DC∥AB． 13．如图，已知点 A、F、E、C 在同一直线上，AB∥CD，∠ABE=∠CDF，AF=CE． （1）从图中任找两组全等三角形；（2）从（1）中任选一组进行证明． 14．在△ABC 中，AB=AC，点 E，F 分别在 AB，AC 上，AE=AF，BF 与 CE 相交于点 P．求证：PB=PC，并直接 写出图中其他相等的线段． 15．如图，已知：在△AFD 和△CEB 中，点 A、E、F、C 在同一直线上，AE=CF，∠B=∠D，AD∥BC．求证： AD=BC． 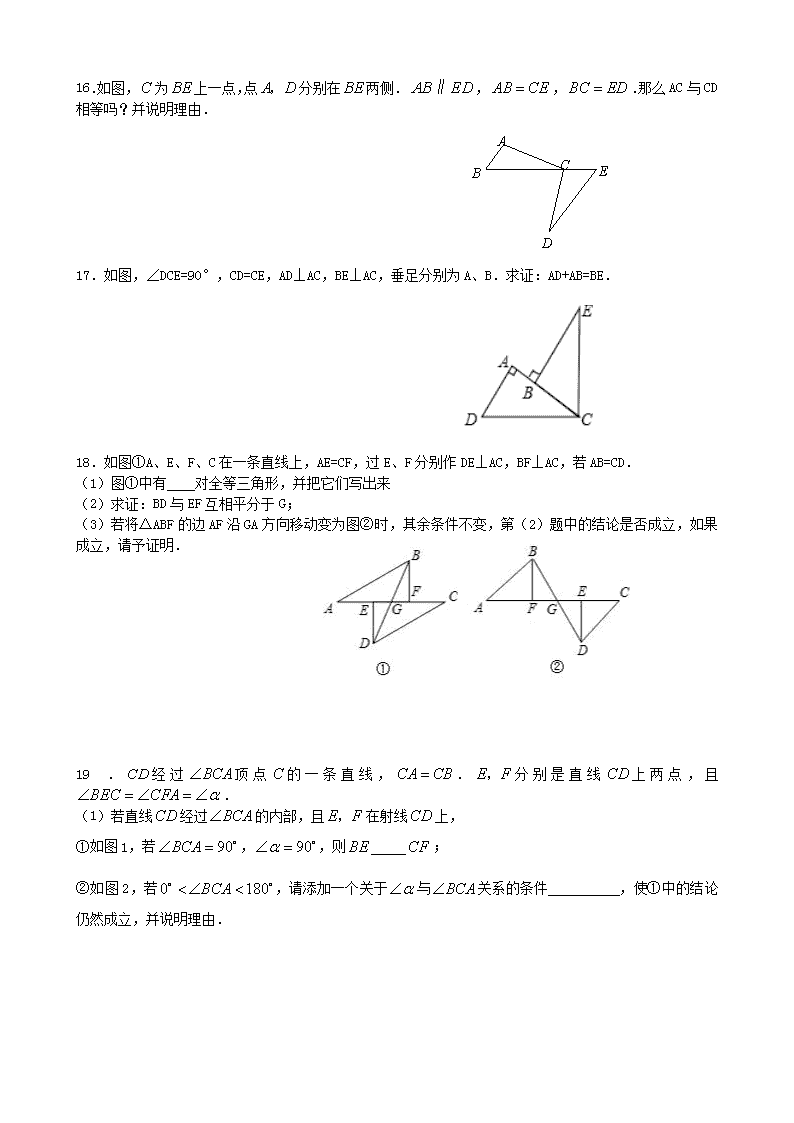16．如图，C 为 BE 上一点，点 A D， 分别在 BE 两侧． AB ED∥ ， AB CE ， BC ED ．那么 AC 与 CD 相等吗？并说明理由． 17．如图，∠DCE=90°，CD=CE，AD⊥AC，BE⊥AC，垂足分别为 A、B．求证：AD+AB=BE． 18．如图①A、E、F、C 在一条直线上，AE=CF，过 E、F 分别作 DE⊥AC，BF⊥AC，若 AB=CD． （1）图①中有 对全等三角形，并把它们写出来 （2）求证：BD 与 EF 互相平分于 G； （3）若将△ABF 的边 AF 沿 GA 方向移动变为图②时，其余条件不变，第（2）题中的结论是否成立，如果 成立，请予证明． 19 ． CD 经 过 BCA 顶 点 C 的 一 条 直 线 ， CA CB ． E F， 分 别 是 直 线 CD 上 两 点 ， 且 BEC CFA      ． （1）若直线 CD 经过 BCA 的内部，且 E F， 在射线CD 上， ①如图 1，若 90BCA   ， 90   ，则 BE CF ； ②如图 2，若 0 180BCA    ，请添加一个关于  与 BCA 关系的条件 ，使①中的结论 仍然成立，并说明理由． A C E D B （2）如图 3，若直线 CD 经过 BCA 的外部， BCA   ，请提出 EF BE AF， ， 三条线段数量关系 的合理猜想： ． 20.如图，已知△ABC 中，AB＝AC＝5 厘米，BC＝4 厘米，点 D 为 AB 的中点．如果点 P 在线段 BC 上以 1.5 厘米/秒的速度由 B 点向 C 点运动，同时，点 Q 在线段 CA 上由 C 点向 A 点运动． （1）若点 Q 的运动速度与点 P 的运动速度相等，经过 1 秒后，△BPD 与△CQP 是否全等，请说明理由； （2）若点 Q 的运动速度与点 P 的运动速度不相等，当点 Q 的运动速度为多少时，能够使△BPD 与△CQP 全 等？ 初二数学寒假作业 2（轴对称图形） 一、精心选一选 1.如图，下列图案是我国几家银行的标志，其中是轴对称图形的有（ ） A .1 个 B. 2 个 C. 3 个 D. 4 个 2.在△ABC 内一点 P 满足 PA=PB=PC，则点 P 一定是△ABC（ ） A.三条角平分线的交点 B.三边垂直平分线的交点 C.三条高的交点 D.三条中线的交点 3.下列语句：①全等三角形的周长相等②面积相等的三角形是全等三角形③若成轴对称的两个图形中的对 称线段所在直线相交,则这个交点一定在对称轴上．其中正确的有( ) A．0 个 B．1 个 C．2 个 D．3 个 4.用直尺和圆规作一个角的平分线的示意图如图所示，则能说明∠AOC＝∠BOC 的依据是( ) A．SSS B．ASA C．AAS D．角平分线上的点到角两边距离相等 A B C E F D D A B C E F A DF C E B （图 1） （图 2） （图 3） 第 4 题图 3 号袋4 号袋 2 号袋1 号袋 第 5 题图 5. 如图是一个经过改造的台球桌面示意图，图中四个角上的阴影部分分别表示四个入球孔。如果一个球 按图中所示的方向被击出（球可以经过多次反射），那么该球最后将落入的球袋是（ ） A、一号袋 B、二号袋 C、三号袋 D、四号袋 6.如图，∠MON 内有一点 P，P 点关于 OM 的轴对称点是 G，P 点关于 ON 的轴对称点是 H，GH 分别交 OM、ON 于 A、B 点，若 GH 的长为 10cm，求△PAB 的周长为（ ） A． 5cm B． 10cm C． 20cm D．15cm 7.如图，∠AOB 的平分线上一点 P 到 OA 的距离为 5，Q 是 OB 上任意一点，则（ ） A．PQ≥5 B．PQ＞5 C．PQ≤5 D．PQ＜5 8.如图，在 2×2 的正方形网格中，有一个格点△ABC（阴影部分），则网格中所有与△ABC 成轴对称的格点三角形的个数为（ ） A．2 B．3 C．4 D．5 二、细心填一填 9. 角的对称轴是 . 10. 等腰三角形的一内角为 40°，则它的底角为 . 11. 如果等腰三角形的两边长为 3cm，6cm，那么它的周长为 . 12. 如图，△ABE≌△ACD，∠ADB=105°，∠B=60°则∠BAE = . 13. 如图，在△ABC 中，BC=8 cm，BP、CP 分别是∠ABC 和∠ACB 的平分线，且 PD∥AB，PE∥AC，则△PDE 的周长是___________cm． 14. 如图，AD 是△ABC 的角平分线，DF⊥AB，垂足为 F，DE=DG，△ADG 和△AED 的面积分别为 49 和 40， 则△EDF 的面积为 ． 15. 如图，在△ABC 中，AB=AC，DE 是 AB 的中垂线，△BCE 的周长为 14，BC=6，则 AB 的长为 ． 16. 如图，∠BAC=1000，MN、EF 分别垂直平分 AB、AC，则∠MAE 的大小为_____________ 17. 在等腰△ABC 中，∠A=36°,则∠B= 18. 如图，CA⊥AB，垂足为点 A，AB=12，AC=6，射线 BM⊥AB,垂足为点 B，一动点 E 从 A 点出发以 2 厘米/ 秒沿射线 AN 运动，点 D 为射线 BM 上一动点，随着 E 点运动而运动，且始终保持 ED=CB，当点 E 经过 秒时，△DEB 与△BCA 全等. 第 8 题图第 7 题图第 6 题图 ED A B C 第 12 题图 第 13 题图 第 14 题图 三、解答题 19.在下列的图形上补一个小正方形，使它成为一个轴对称图形 20.如图：某通信公司在 A 区要修建一座信号发射塔 M，要求发射塔到两城镇 P、Q 的距离相等，同时到两 条高速公路 l1、l2 的距离也相等．在图中作出发射塔 M 的位置．（不写作法，保留作图痕迹） 21.如图,在一小水库的两测有 A、B 两点，A、B 间的距离不能直接测得，采用方法如下：取一点可以同时 到达 A、B 的点 C，连结 AC 并延长到 D，使 AC=DC；同法，连结 BC 并延长到 E，使 BC=EC；这样，只要测量 DE 的长度，就可以得到 A、B 的距离了，这是为什么呢？根据以上的描述，请画出图形， 并写出已知、求 证、证明。 A· ·B C. 第 15 题图 F E M N C B A 第 16 题图 第 18 题图 B NE D A C M A D B CE F 22.如图，线段 AB 经过线段 CD 的中点 E，且 AC＝AD，求证：BC＝BD. 23.在△ABC 中，AB 边的垂直平分线 l1 交 BC 于 D，AC 边的垂直平分线 l2 交 BC 于 E，l1 与 l2 相交于点 O．△ADE 的周长为 6cm． （1）求 BC 的长； （2）分别连结 OA、OB、OC，若△OBC 的周长为 16cm，求 OA 的长． 24.如图，在△ABC 中，AB=AC，点 D、E、F 分别在 AB、BC、AC 边上，且 BE=CF，BD=CE. （1）求证：△DEF 是等腰三角形；（2）当∠A=40°时，求∠DEF 的度数； 25. 如图，△ABC 中，AB=AC=2，∠B=∠C=40°．点 D 在线段 BC 上运动（点 D 不与 B、C 重合）， 连接 AD， 作∠ADE=40°，DE 交线段 AC 于 E． （1）当∠BAD=20°时，∠EDC= °； （2）当 DC 等于多少时，△ABD≌△DCE?试说明理由； (3)△ADE 能成为等腰三角形吗？若能，直接写出此时∠BAD 的度数；若不能，请说明理由． A B C DE A B CD E 初二数学寒假作业 3（勾股定理） 一、选择题 1．一个直角三角形，两直角边长分别为 3 和 4，下列说法正确的是（ ） A．斜边长为 5 B．三角形的周长为 25 C．斜边长为 25 D．三角形的面积为 20 2．下列各组数中不能作为直角三角形的三边长的是（ ） A．1.5，2，3 B．7，24，25 C．6，8，10 D．9，12，15 3．直角三角形两直角边长度为 5，12，则斜边上的高（ ） A．6 B.8 C. 13 18 D. 13 60 4．小明想知道学校旗杆的高度，他发现旗杆上的绳子垂到地面还多 1 米，当他把绳子的下端拉开 5 米后， 发现下端刚好接触地面，则旗杆的高是（ ） A．8 米 B．10 米 C．12 米 D．14 米 5．在△ABC 中，∠C=90°，周长为 60，斜边与一直角边比是 13：5，则这个三角形三边长分别是（ ） A．5，4，3 B．13，12，5 C．10，8，6 D．26，24，10 6．下列各组线段中的三个长度：①9，12，15；②7，24，25；③32，42，52；④3a，4a，5a（a＞0）； ⑤m2﹣n2，2mn，m2+n2（m，n 为正整数，且 m＞n）其中可以构成直角三角形的有（ ） A．5 组 B．4 组 C．3 组 D．2 组 7．下列结论错误的是（ ） A．三个角度之比为 1：2：3 的三角形是直角三角形 B．三个边长之比为 3：4：5 的三角形是直角三角形 C．三个边长之比为 8：16：17 的三角形是直角三角形 D．三个角度之比为 1：1：2 的三角形是直角三角形 8．小明准备测量一段河水的深度，他把一根竹竿竖直插到离岸边 1.5m 远的水底，竹竿高出水面 0.5m， 把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，则河水的深度为（ ） A． 2m B．2.5m C．2.25m D．3m 9．小军量得家里新购置的彩电荧光屏的长为 58 厘米，宽为 46 厘米，则这台电视机的尺寸是（实际测量 的误差可不计）（ ） A．9 英寸（23 厘米） B．21 英寸（54 厘米） C．29 英寸（74 厘米） D．34 英寸（87 厘米） 10．观察下列几组数据：（1）8，15，17；（2）7，12，15；（3）12，15，20；（4）7，24，25．其 中能作为直角三角形三边长的有（ ）组． A． 1 B．2 C．3 D．4 二、填空题 11．在 Rt△ABC 中，∠C=90°，（1）若 a=5，b=12，则 c= ；（2）b=8，c=17，则 S△ABC= ． 12． 如果梯子的底端离建筑物 9 米，那么 15 米长的梯子可以到达建筑物的高度是 米． 13． 已知|x﹣6|+|y﹣8|+（z﹣10）2=0，则由此 x，y，z 为三边的三角形面积为 ． 14． 在△ABC 中，若三边长分别为 9，12，15，则以这样的三角形拼成的矩形面积为 ． 15．△ABC 中，AB=AC=17cm，BC=16cm，则高 AD= cm． 16．如图所示的线段的长度或正方形的面积为多少．（注：下列各图中的三角形均为直角三角形）． 答：A= ，y= ，B= ． 17．已知一个 Rt△的两边长分别为 3 和 4，则第三边长是 ． 18．求图中直角三角形中未知的长度：b= ，c= ． 19．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为 7cm， 则正方形 A，B，C，D 的面积之和为 cm2． 20．已知三角形的三边长分别是 2n+1，2n2+2n，2n2+2n+1，则最大角是 度． 三、解答题 21．做一做，如图每个小方格都是边长为 1 的正方形，求图中格点四边形 ABCD 的面积． 22．如图，一直角三角形三边长分别为 6，8，10，且是三个圆的直径，求阴影部分面积（结果保留π） 23．一个三角形的三边长的比为 3：4：5，那么这个三角形是直角三角形吗，为什么？ 24．如图所示，为修铁路需凿通隧道 AC，测得∠A=53°，∠B=37°．AB=5km，BC=4km，若每天凿 0.3km， 试计算需要几天才能把隧道 AC 凿通？ 25．观察下列表格：请你结合该表格及相关知识，求出 b，c 的值． 列举 猜想 3、4、5 32=4+5 5、12、13 52=12+13 7、24、25 72=24+25 … … 35、b、c 352=b+c 26．如图所示的一块地，∠ADC=90°，AD=12m，CD=9m，AB=39m，BC=36m，求这块地的面积． 27．如图，在边长为 c 的正方形中，有四个斜边为 c 的全等直角三角形，已知其直角边长为 a，b．利用 这个图试说明勾股定理． 28．如图，某游泳池长 48 米，小方和小杨进行游泳比赛，从同一处（A 点）出发，小方平均速度为 3 米/ 秒，小杨为 3.1 米/秒．但小杨一心想快，不看方向沿斜线（AC 方向）游，而小方直游（AB 方向），两人 到达终点的位置相距 14 米．按各人的平均速度计算，谁先到达终点，为什么？ 初二数学寒假作业 4（实数） 一、选择题： 1．下列各式中，正确的是 （ ） A.  22 2   ；B.  23 9  ；C.  29 3   ；D.  213 13  ； 2．下列各数中，互为相反数的一组是 （ ） A.-2 与 3 8 ；B. -2 与  22 ；C. -2 与 1 2  ；D. 2 与 2； 3．某种鲸的体重约为 51.36 10 ㎏，关于这个近似数，下列说法正确的是 （ ） A．它精确到百位；B．它精确到 0.01；C．它精确到千分位；D．它精确到千位； 4．一直角三角形的两边长分别为 3 和 4，则第三边的长为 （ ） A．5； B． 7 ；C． 5 ； D．5 或 7 ； 5．若规定误差小于 1，那么 60 的估算值为 （ ） A．3； B．7； C．8； D．7 或 8； 6．和数轴上的点一一对应的是 （ ） A.整数；B.有理数；C.无理数；D.实数； 7．若  21 2 0x y    ，则 2014x y 等于 （ ） A.-1；B.1；C. 20143 ；D. 20143 ； 8．若 2 7a  与3 3a  是同一个数的平方根，则 a 的值是 （ ） A． 2； B．-4； C．2 或-4； D．-2； 9．如图，数轴上 1 和 2 的对应点分别为 A、B，A 是线段 BC 的中点，则点 C 对应的实数为 （ ） A． 2 2 ； B． 2 1 ； C． 2 2 ； D．1 2 ； 10．如图，M、N、P、Q 是数轴上的四个点，这四个点中最适合表示 7 的点是 （ ） A．M； B．N； C．P； D．Q； 二、填空题： 11． 当 x 时， 3x  有平方根. 3 5 2 6 ； 5 6 6 5 ；（用“＞”或“＜”） 12．实数 22 7 ， 7 ， 8 ， 3 2 ， 36 ， 3  中的无理数是 . 13． 2 5 的绝对值是 ，1 2 的相反数是 ， 3 的倒数是 . 14． 16 的平方根是 ， 25 的算术平方根是 ，绝对值最小的实数是 . 15．若 22 m nx y 与 4 23 m nx y  是同类项，则 3m n 的立方根是 . 第 10 题图 16．若 13a b  ，且 a、b 为连续正整数，则 b2-a2= . 17．如图，正方形 ODBC 中，OC=1，OA=OB，则数轴上点 A 表示的数是 ． 18．规定用符号[x]表示一个实数 x 的整数部分，例如：[3.69]=3， 3 1    .按此规定， 13 1   = . 三、解答题： 19．求下列各式的值： （1）  38 1 27 0x    （2）  225 2 36 0x    （3） 22 1 16x   ； 20． 计算： （1）   0 1 2 2 3 12 43 2               ； （2）  2 33 1 8 3 1 3 2       ； 21．用直尺和圆规在如图所示的数轴上作出表示 13 的点. 22．如图， a 、b 、 c 分别是数轴上 A、B、C 所对应的实数.试化简  32 3c a b a b b c      . 23．已知 2a-1 的平方根是±3，3a+b-1 的平方根是±4，求 a+2b 的平方根. 第 17 题图 24．实数 a b， 互为相反数， c d， 互为倒数， 6x  ，求代数式  2 2 3x a b cd x a b cd      的值. 25．正方形网格中的每个小正方形的边长都是 1，每个小格的顶点叫做格点，以格点为顶点，（1）在图 ①中，画一个面积为 10 的正方形；（2）在图②、图③中，分别画两个不全等的直角三角形，使它们的三 边长都是无理数． 26．（1）已知 3x y  与 1x y  互为相反数，求 2x y 的平方根. （2）已知 24 24 8y x x     ，求 3 5x y 的值. 27．阅读下面的文字，解答问题： 大家知道 2 是无理数，而无理数是无限不循环小数，因此 2 的小数部分我们不可能全部地写出来，于 是小明用 2 1 来表示 2 的小数部分，你同意小明的表示方法吗？ 事实上，小明的表示方法是有道理的，因为 2 的整数部分是 1，将这个数减去其整数部分，差就是小数 部分．又例如：∵ 4 7 9  ，即 2＜ 7 ＜3，,∴ 7 的整数部分为 2，小数部分为( 7 2 )． 请解答：（1）如果 5 的小数部分为 a ， 13 的整数部分为b ，求 5a b  的值； （2）已知：10 3 x y   ，其中 x 是整数，且 0＜y＜1，求 x-y 的相反数． 初二数学寒假作业 5（平面直角坐标系） 一、选择题： 1．如图，已知棋子“车”的坐标为（-2，-1），棋子“马”的坐标为（1，-1），则棋子“炮”的坐标为（ ） A．（3，2） B．（-3，2） C．（3，-2） D．（-3，-2） 2．在平面直角坐标系中，若点 P (a,b)在第二象限，则点 Q(2-a,-1-b)在 （ ） A．第一象限； B．第二象限； C．第三象限； D．第四象限； 3．如果点 P(-2,b)和点 Q(a,-3)关于 x 轴对称，则 a+b 的值是 （ ） A．-1； B．1； C．-5； D．5； 4．点 P（-2，-3）向左平移 1 个单位，再向上平移 3 个单位，则所得到的点的坐标为（ ） A．（-3，0）； B．（-1，6）； C．（-3，-6）； D．（-1，0）； 5．如图，在平面直角坐标系中，点 B、C、E、在 y 轴上，Rt△ABC 经过变换得到 Rt△ODE．若点 C 的 坐标为（0，1），AC=2，则这种变换可以是 （ ） A．△ABC 绕点 C 顺时针旋转 90°，再向下平移 3； B．△ABC 绕点 C 顺时针旋转 90°，再向下平移 1； C．△ABC 绕点 C 逆时针旋转 90°，再向下平移 1； D．△ABC 绕点 C 逆时针旋转 90°，再向下平移 3； 6．如图，在 5×4 的方格纸中，每个小正方形边长为 1，点 O，A，B 在方格纸的交点（格点）上，在第四 象限内的格点上找点 C，使△ABC 的面积为 3，则这样的点 C 共有 （ ） A．2 个 B．3 个 C．4 个 D．5 个 7．已知点 M（3,2）与点 N(x,y)在同一条平行于 x 轴的直线上,且点 N 到 y 轴的距离为 5，则点 N 的坐标 为 （ ） A．（2，5）；B．（5，2）； C．（-5，2）；D．（-5，2）或（5，2）； 8．在平面直角坐标系中，已知 A（2，2），在 x 轴上确定一点 P，使△AOP 为等腰三角形，则符合条件 的点 P 有 （ ） A．2 个； B．3 个； C．4 个； D．5 个； 第 1 题图 第 5 题图 第 9 题图第 6 题图 9．如图，在平面直角坐标系中，A（1，1），B（-1，1），C（-1，-2），D（1，-2）．把一条长为 2014 个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点 A 处，并按 A-B-C-D-A…的规律绕在 四边形 ABCD 的边上，则细线另一端所在位置的点的坐标是( ) A．（-1，0） B．（1，-2） C．（1，1） D．（-1，-1） 10．在平面直角坐标系中，对于平面内任一点（a，b），若规定以下三种变换： ①△（a，b）=（-a，b）； ②O（a，b）=（-a，-b）；③Ω（a，b）=（a，-b）； 按照以上变换有：△（O（1，2））=（1，-2），那么 O（Ω（3，4））等于 （ ） A．（3，4） B．（3，-4） C．（-3，4） D．（-3，-4） 二、填空题： 11．若点 M(m-3,m+1)在平面直角坐标系的 x 轴上，则点 M 的坐标是 . 12．已知点 P (a,2a+3)点在第二、四象限的角平分线上，则 a = . 13．点 P（2，3）到 x 轴的距离是 ；点 Q（5，-12）到原点的距离是 .点 C 到 x 轴 的距离为 1，到 y 轴的距离为 3，且在第三象限，则点 C 的坐标是 . 14．在直角坐标系中，点 A（3，4）和点 B（a，b）关于原点对称，则 a-b 的值为 ． 15．在平面直角坐标系中，已知点 A（m，3）与点 B（4，n）关于 y 轴对称，那么(m+n)2015 的值为 . 16．若第二象限内的点 P(x,y)满足|x|=3，y2=25，则点 P 的坐标是 ． 17．如图，△ABC 的顶点都在正方形网格格点上，点 A 的坐标为（-1，4）．将△ABC 沿 y 轴翻折到第一象限，则点 C 的对应点 C′的坐标是 ． 18．如图，在平面直角坐标系中，点 A、B、C 的坐标分别是（-1，-1）、（0，2）、（2，0），点 P 在 y 轴上，且坐标为（0，-2）．点 P 关于点 A 的对称点为 P1，点 P1 关于点 B 的对称点为 P2，点 P2 关于点 C 的对称点为 P3，点 P3 关于点 A 的对称点为 P4，点 P4 关于点 B 的对称点为 P5，点 P5 关于点 C 的对称 点为 P6，点 P6 关于点 A 的对称点为 P7…，按此规律进行下去，则点 P2016 的坐标是 ． 三、解答题： 19．已知点 P(2x-1,3x-9)在第四象限，化简 2 26 9 4 4 1x x x x     . 20．如图，平行四边形 ABCD 的边长 AB=4，BC=2，若把它放在直角坐标系内，使 AB 在 x 轴上，点 C 在 y 轴上，点 A 的坐标是（-3，0），求点 B、C、D 的坐标． 第 17 题图 第 18 题图 21．如图，在平面直角坐标系中，△ABC 的三个顶点都在格点上，点 A 的坐标为（2，4），请解答下列 问题： （1）画出△ABC 关于 x 轴对称的△A1B1C1，并写出点 A1 的坐标． （2）画出△A1B1C1 先向左平移 3 个单位长度，再向上 平移 4 个单位长度得到的△A2B2C2 并写出点 A2 的坐 标． 22．已知边长为 2 的正方形 OABC 在直角坐标系中，（如图）OA 与 y 轴的夹角为 30°，求点 A、点 C、 点 B 的坐标． 23．如图，A（-1，0），C（1，4），点 B 在 x 轴上，且 AB=3． （1）求点 B 的坐标，并画出△ABC； （2）求△ABC 的面积． 24．已知点 A (-3,y)与点 B(x,2)关于 y 轴对称，点 C 在直线 AB 上，且点 C 到 y 轴的距离为 2，试写出点 C 的坐标 25．在平面直角坐标系内，A、B、C 三点的坐标分别是 A（5，0）、B（0，3）、C（5，3），O 为坐标 原点，点 E 在线段 BC 上，若△AEO 为等腰三角形，求点 E 的坐标． 26．在△ABC 中，∠ACB=90°，∠BAC=60°，AC=2，如图，以 AB 所在直线为 x 轴，以 AB 的垂直平分 线为 y 轴，建立直角坐标系，求点 A、B、C 的坐标. 27． 如图，OABC 是一张放在平面直角坐标系中的长方形纸片，O 为原点，点 A 在 x 轴的正半轴上，点 C 在 y 轴的正半轴上，OA=10，OC=8，在 OC 边上取一点 D，将纸片沿 AD 翻折，使点 O 落在 BC 边上 的点 E 处，求 D、E 两点的坐标． 初二数学寒假作业 6（一次函数） 一、选择题 1．若函数 y=（k+1）x+k2﹣1 是正比例函数，则 k 的值为（ ） A．0 B．1 C．±1 D．﹣1 2．（4 分）下列函数中 y 随 x 的增大而减小的是（ ） A．y=x﹣m2 B．y=（﹣m2﹣1）x+3 C．y=（|m|+1）x﹣5 D．y=7x+m 3．（4 分）已知一次函数 y=kx﹣k，y 随 x 的增大而减小，则函数图象不过第（ ）象限． A．第一象限 B．第二象限 C．第三象限 D．第四象限 4．（4 分）要由直线 得到直线 ，直线 应（ ） A．向上平移 5 个单位 B．向下平移 5 个单位 C．向上平移 个单位 D．向下平移 个单位 5．若直线 y=kx+b 经过 A（0，2）和 B（3，0）两点，那么这个一次函数关系式是（ ） A．y=2x+3 B． C．y=3x+2 D．y=x﹣1 6．张大伯出去散步，从家走了 20 分钟，到一个离家 900 米的阅报亭，看了 10 分钟报纸后，用了 15 分 钟返回到家，下面哪个图形表示张大伯离家时间与距离之间的关系（ ） A． B． C． D． 7．要从 的图象得到直线 ，就要将直线 （ ） A．向上平移 个单位 B．向下平移 个单位 C．向上平移 2 个单位 D 向下平移 2 个单位 8．如图一次函数 y1=ax+b 和 y2=cx+d 在同一坐标系内的图象，则 的解 中（ ） A．m＞0，n＞0 B．m＞0，n＜0 C．m＜0，n＞0 D．m＜0，n＜0 9．两个一次函数 y1=mx+n，y2=nx+m，它们在同一坐标系中的图象可能是图中的（ ） A． B． C． D． 10．如图,一次函数 y=kx+b 的图象与正比例函数 y=2x 的 图象平行,且经过点 A（1，﹣2），则 kb= ． A．6 B．8 C．-6 D．﹣8 二、填空题 11．如果直线 y=kx+b 经过第一、三、四象限，那么直线 y=﹣bx+k 经过第 象限． 12．通过平移把点 A（2，﹣3）移到点 A′（4，﹣2），按同样的平移方式，点 B（3，1）移到点 B′，则 点 B′的坐标是 ． 13．要把直线 y=3x﹣2 向上平移，使其图象经过点（2，10），需要向 平移 个 单位． 14．已知一次函数 y=﹣2x+3 中，自变量取值范围是﹣3≤x≤8，则当 x= 时，y 有最大 值 ． 15．已知点 A（3，0）、B（0，﹣3）、C（1，m）在同一条直线上，则 m= ． 16．已知直线 y=2x﹣4，则此直线与两坐标轴围成的三角形面积为 ． 17．已知一次函数 y=（m+2）x+1，函数 y 的值随 x 值的增大而增大，则 m 的取值范围是 ． 18．已知一次函数 y=2x+4 的图象经过点（m，8），则 m= ． 19．直线 y=3x﹣1 与直线 y=x﹣k 的交点在第四象限，k 的取值范围是 ． 20．若一次函数 y=kx+b 的图象经过（﹣2，﹣1）和点（1，2），则这个函数的图象不经过 象 限． 三、解答题 21．在某地，人们发现某种蟋蟀 1 分钟所叫次数与当地温度之间近似为一次函数关系．下面是蟋蟀所叫次 数与温度变化情况对照表： 蟋蟀叫次数 … 84 98 119 … 温度（℃） … 15 17 20 … （1）根据表中数据确定该一次函数的关系式； （2）如果蟋蟀 1 分钟叫了 63 次，那么该地当时的温度大约为多少摄氏度？ 22．已知直线 l 经过点（﹣1，5），且与直线 y=﹣x 平行．（1）求直线 l 的解析式；（2）若直线 l 分别 交 x 轴、y 轴于 A、B 两点，求△AOB 的面积． 23．甲骑自行车、乙骑摩托车沿相同路线由 A 地到 B 地，行驶过程中路程与时间的函数关系的图象如图．根 据图象解决下列问题： （1）谁先出发先出发多少时间谁先到达终点先到多少时间？ （2）分别求出甲、乙两人的行驶速度； （3）在什么时间段内，两人均行驶在途中（不包括起点和终点）在这一时间段内，请你根据下列情形， 分别列出关于行驶时间 x 的方程或不等式（不化简，也不求解）：①甲在乙的前面；②甲与乙相遇；③甲 在乙后面． 24．有一个附有进水管、出水管的水池，每单位时间内进出水管的进、出水量都是一定的，设从某时刻开 始，4h 内只进水不出水，在随后的时间内不进水只出水，得到的时间 x（h）与水量 y（m3）之间的关系 图（如图）．回答下列问题：X k B 1 . c o m (1)进水管 4h 共进水多少？每小时进水多少？(2)当 0≤x≤4 时，y 与 x 有何关系？(3)当 x=9 时，水池中的水 量是多少？(4)若 4h 后，只放水不进水，那么多少小时可将水池中的水放完？ 25．某生物小组观察一植物生长，得到植物高度 y（单位：厘米）与观察时间 x（单位：天）的关系，并 画出如图所示的图象（AC 是线段，直线 CD 平行 x 轴）． （1）该植物从观察时起，多少天以后停止长高？ （2）求直线 AC 的解析式，并求该植物最高长多少厘米？ 26．某商场筹集资金 12.8 万元，一次性购进空调、彩电共 30 台．根据市场需要，这些空调、彩电可以全 部销售，全部销售后利润不少于 1.5 万元，其中空调、彩电的进价和售价见表格． 空调 彩电 进价（元/台） 5400 3500 售价（元/台） 6100 3900 设商场计划购进空调 x 台，空调和彩电全部销售后商场获得的利润为 y 元． （1）试写出 y 与 x 的函数关系式； （2）商场有哪几种进货方案可供选择？ （3）选择哪种进货方案，商场获利最大？最大利润是多少元？ 初二数学寒假作业 7（综合训练一） 一、选择题（本题共 8 小题，每小题 2 分，共 16 分） 1．如图所示，图中不是轴对称图形的是( ) A． B． C． D． 2．在△ABC 中，∠A，∠B、∠C 的对应边分别是 a、b、c，若∠C=90°，则下列等式中成立的是( ) A．a2+b2=c2 B．b2+c2=a2 C．a2+c2=b2 D．b2﹣a2=c2 3．一个等腰三角形的两边长分别是 3 和 7，则它的周长为( ) A．17 B．15 C．13 D．13 或 17 4．下列各组数中不能作为直角三角形三边长的是( ) A．3，4，5 B．4，5，6 C．5，12，13 D．12，16，20 5．已知△ABC≌△DEF，∠A=80°，∠E=40°，则∠F 等于( ) A．80° B．40° C．120° D．60° 6．如图，若 MB=ND，∠MBA=∠NDC，下列条件中不能判定△ABM≌△CDN 的是( ) A．AM=CN B．AM∥CN C．AB=CD D．∠M=∠N 第 6 题图 第 7 题图 第 8 题图 7．如图，△ABC 中，AB=5，AC=8，BD，CD 分别平分∠ABC，∠ACB，过点 D 作直线平行于 BC，交 AB，AC 于 E，F，则△AEF 的周长为( ) A．12 B．13 C．14 D．18 8．勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如 图 1 是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图 2 是由图 1 放入 矩形内得到的，∠BAC=90°，AB=3，AC=4，点 D，E，F，G，H， I 都在矩形 KLMJ 的边上，则矩形 KLMJ 的面积为( ) A．90 B．100 C．110 D．121 二、填空题（本题共 10 小题，每小题 3 分，共 30 分，） 9．在镜子中看到时钟显示的是， ，则实际时间是 ． 10．若等腰三角形的一个角为 50°，则它的顶角为 ． 11．在直角△ABC 中，∠ACB=90°，D 是 AB 的中点，CD=3cm，则 AB= cm． 12．等腰△ABC 中，AB=AC=10cm，BC=12cm，则 BC 边上的高是 cm． 13．如图，已知△ABC≌△DEC，则∠A=∠D，BC= ． 14．如图，AE=BF，AD∥BC，AD=BC，则 DF= ． 第 13 题图 第 14 题图 第 15 题图 15 ． 如 图 ， 已 知 AB=AD ， ∠1=∠2 ， 要 使 △ABC≌△ADE ， 还 需 添 加 的 条 件是 （ 只 需 填 一 个 ） ________________________. 16．如图所示，AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3= ． 17．有一个边长为 10 尺的正方形池塘，一棵芦苇生长在它的正中央，高出水面的部分为 1 尺，如果把该 芦 苇 的 顶 端 沿 水 池 边 垂 直 的 方 向 拉 到 岸 边 ， 发 现 芦 苇 顶 端 恰 与 水 面 齐 平 ， 则 芦 苇 的 长 度 是 尺． 第 16 题图 第 18 题图 18．如图，在△ABC 中，∠ACB=90°，∠BAC=40°，在直线 AC 上找点 P，使△ABP 是等腰三角形，则 ∠APB 的度数为 ． 三、解答题（本题共 9 小题，共 74 分） 19．如图，五边形 ABCDE 是轴对称图形，线段 AF 所在直线为对称轴，找出图中所有相等的线段和相等 的角． 20．作图题：如图所示是毎一个小方格都是边长 为 1 的正方形网格． ①在 BC 上找一点 P，使点 P 到 AB 和 AC 的距 离相等； ②在射线 AP 上找一点 Q，使 QB=QC． 21．如图，点 E、F 在 BC 上，BE=FC，AB=DC，∠B=∠C．求证：∠A=∠D． 22．已知，如图，AD=BC，AC=BD，AC 与 BD 相交于点 E． 求证：△EAB 是等腰三角形． 23．如图，已知 AB=AC=AD，∠CBD=2∠BDA，∠BAC=48°． （1）求∠ABC 的度数； （2）求∠CAD 的度数． 24．如图，△ABC 中，BC=10，AB 的垂直平分线分别交 AB、BC 于点 D、E，AC 的垂直平分线分别交 AC、BC 于点 F、G．求△AEG 的周长． 25．八年级二班小明和小亮同血学习了“勾股定理”之后，为了测得得如图风筝的高度 CE， 他们进行了如下操作： （1）测得 BD 的长度为 15 米．（注：BD⊥CE） （2）根据手中剩余线的长度计算出风筝线 BC 的长为 25 米． （3）牵线放风筝的小明身高 1.6 米．求风筝的高度 CE． 26．如图，AB∥CD，AB=CD．AD、BC 相交于点 O，OE=OF，BE、CF 分别交 AD 于点 E、F．根据以 上信息：（1）请说出图中共有哪几对全等三角形；（2）证明：BE=CF． 27．如图，在△ABC 中，BA=BC，D 在边 CB 上，且 DB=DA=AC． （1）如图 1，填空∠B= °，∠C= °； （2）若 M 为线段 BC 上的点，过 M 作直线 MH⊥AD 于 H，分别交直线 AB、AC 与点 N、E，如图 2①求 证：△ANE 是等腰三角形；②试写出线段 BN、CE、CD 之间的数量关系，并加以证明． 初二数学寒假作业 8（综合训练二） 一、填空题（本大题共有 12 小题，每小题 2 分，共计 24 分） 1．4 的平方根是 ． 2．比较大小： 15  4（填“>”、“<”或“=”）． 3．点 A（－4 , 3）到 y 轴的距离是 ． 4．若点（m , n）在函数 y=2x+1 的图象上，则 2m-n＝ ． 5．数 2.18×106 精确到 位． 6．直线 y=3x-6 与坐标轴围成的三角形面积为 ． 7. 在平面直角坐标系中，已知点 A、B 的坐标分别为 A (1，0)、B (3，1) ，AB 的长度为 ． 8．如图，ΔABC 中，AB＝AC，AB 的垂直平分线交 AC 于 P 点．若 AB＝5 cm，BC＝3 cm，则ΔPBC 的 周长＝ ． 9．如图，已知直线 y=ax+b 和直线 y=kx 交于点 P（-4，-2），则关于 x，y 的二元一次方程组 , . y ax b y kx     的解是 ． （第 8 题图） （第 9 题图） （第 11 题图） （第 12 题图） 10．无论 a 取什么实数，点 A（2a ，4a+1）都在直线 l 上，则直线 l 的表达式是 ． 11．如图：在△ABC 中， 5 ACAB ， 4BC ，AD 是△ABC 的中线，AE 是∠BAD 的角平分线， DF∥AB 交 AE 的延长线于点 F，则 DF 的长为 ． 12．如图，已知△ABC 中，AB＝AC，∠BAC＝90º，直角∠EPF 的顶点 P 是 BC 的中点，两边 PE、PF 分别交 AB、AC 于点 E、F，给出以下四个结论： ①AE＝CF； ②△EPF 是等腰直角三角形；③S△ABC =2S 四边形 AEPF；④EF＝AP． 上述结论始终正确的有 ．（填写序号） 二、选择题（本大题共有 7 小题，每小题 3 分，共计 21 分） 13．下列图形中，是轴对称图形的是（ ） 14．点 P（-1，2）关于 y 轴对称的点的坐标为（ ） A．（1，－2） B．（－1，－2） C．（1，2） D．（2，1） 15．已知等腰三角形的两条边长分别为 2 和 5，则它的周长为 A． 9 B． 12 C． 9 或 12 D． 5 16．在下列实数中：3.14，-2， 2 ，0， 2 3 ， ， 22 7 ， 9 ，-1.010010001…，其中无理数有（ ） A．1 个 B．2 个 C． 3 个 D． 4 个 17．P1（x1，y1），P2（x2，y2）是正比例函数 y=-0.5x 图象上的两点，下列判断中，正确的是（ ） A．y1＞y2 B．y1＜y2 C．当 x1＜x2 时，y1＜y2 D．当 x1＜x2 时，y1＞y2 18．如图，∠BAC = 110°，若 MP 和 NQ 分别垂直平分 AB 和 AC，则∠PAQ 的度数是（ ）A．20° B．40° C．50° D．60°2-1-c-n-j-y （第 18 题图） （第 19 题图） 19．如图所示，已知△ABC 中，AB=6，AC=9，AD⊥BC 于 D，M 为 AD 上任一点，则 MC2-MB2 等于（ ） A．9 B．35 C．45 D．无法计算 三、解答题（本大题共有 7 小题，共计 55 分） 20. 计算、解方程（本题满分 8 分，每小题 4 分）： （1） 4 9 8 116 3  （2） 22( 2) 8x   C N M P A B 21．（本题满分 6 分）如图，点 P 是∠ABC 的平分线上一点，PM⊥AB，PN⊥BC，垂足分别是 M、N．求 证：（1）∠PMN＝∠PNM；（2）BM＝BN； 22．（本题满分 7 分）如图所示，已知 AE⊥AB，AF⊥AC，AE=AB，AF=AC. 求证：（1）EC=BF；（2）EC⊥BF． 23．（本题满分 7 分）如图，将长方形 ABCD 沿着对角线 BD 折叠，使点 C 落在 C’处， BC’ 交 AD 于点 E． （1）试判断△BDE 的形状，并说明理由； （2）若 AB=4,AD=8，求△BDE 的面积． 24．（本题满分 9 分）在如图的方格中，每个小正方形的边长都为 1，△ABC 的顶点均在格点上．在建立 平面直角坐标系后，点 B 的坐标为（－1，2）． （1）把△ABC 向下平移 8 个单位后得到对应的△A1B1C1，画出△A1B1C1； （2）画出与△A1B1C1 关于 y 轴对称的△A2B2C2； （3）若点 P（a ，b）是△ABC 边上任意一点，P2 是△△A2B2C2 边上与 P 对应的点，写出 P2 的坐标 为 ； （4）试在 y 轴上作出点 Q，使点 Q 到 B2、 C2 两点的距 离 之 和 最 小 ， QB2+QC2 的 最 小 值 为 ． x y C A B O y（千米） x(小时)106O 600 轿车 客车 25．（本题满分 8 分）一辆客车从甲地开往乙地，一辆轿车从乙地开往甲地，两车同时出发，两车行驶 x 小时后，记客车离甲地的距离为 y1 千米，轿车离甲地的距离为 y2 千米，y1、y2 关于 x 的函数图像如图所 示：（1）根据图像，求 y1、y2 关于 x 的函数关系式； （2）当两车相遇时，求此时客车行驶的时间；（3）两车相距 200 千米时，求客车行驶的时间． 26．（本题满分 10 分）如图，平面直角坐标系中，直线 AB： bxy  3 1 交 y 轴于点 A（0，1），交 x 轴于点 B．过点 E（1，0）作 x 轴的垂线 EF 交 AB 于点 D，P 是直线 EF 上一动点，且在点 D 的上方， 设 P（1， n ）．（1）直线 AB 的表达式为 ；（2）求△ABP 的面积（用含 n 的代数式表示）； （3）当 S△ABP=2 时，以 PB 为边在第一象限作等腰 Rt△BPC，请直接写出点 C 的坐标． 备用图