初中数学苏科八上第6章测试卷 8页

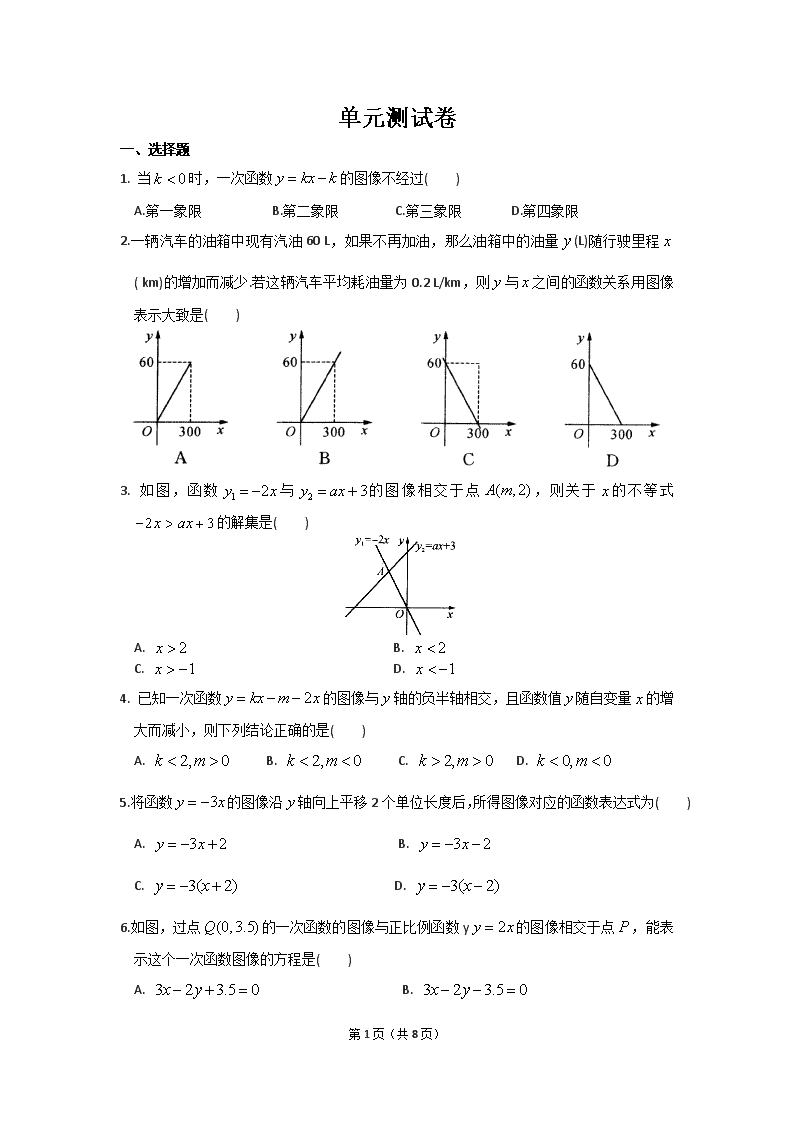
第 1页（共 8页） 单元测试卷 一、选择题 1. 当 0k  时，一次函数 y kx k  的图像不经过( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.一辆汽车的油箱中现有汽油 60 L，如果不再加油，那么油箱中的油量 y (L)随行驶里程 x ( km)的增加而减少.若这辆汽车平均耗油量为 0.2 L/km，则 y 与 x 之间的函数关系用图像 表示大致是( ) 3. 如图，函数 1 2y x  与 2 3y ax  的图像相交于点 ( ,2)A m ，则关于 x 的不等式 2 3x ax   的解集是( ) A. 2x  B. 2x  C. 1x   D. 1x   4. 已知一次函数 2y kx m x   的图像与 y 轴的负半轴相交，且函数值 y 随自变量 x 的增 大而减小，则下列结论正确的是( ) A. 2, 0k m  B. 2, 0k m  C. 2, 0k m  D. 0, 0k m  5.将函数 3y x  的图像沿 y 轴向上平移 2 个单位长度后，所得图像对应的函数表达式为 ( ) A. 3 2y x   B. 3 2y x   C. 3( 2)y x   D. 3( 2)y x   6.如图，过点 (0,3.5)Q 的一次函数的图像与正比例函数 y 2y x 的图像相交于点 P ，能表 示这个一次函数图像的方程是( ) A. 3 2 3.5 0x y   B. 3 2 3.5 0x y   C. 3 2 7 0x y   D. 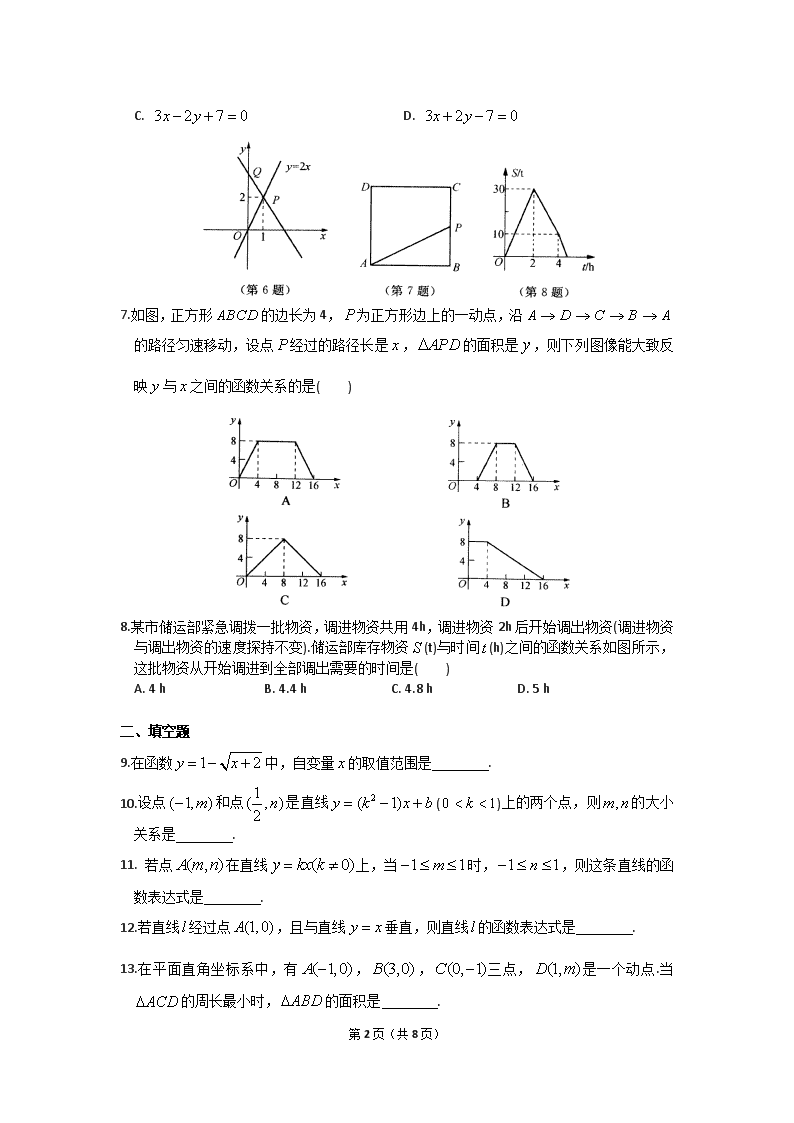3 2 7 0x y   第 2页（共 8页） 7.如图，正方形 ABCD 的边长为 4，P 为正方形边上的一动点，沿 A D C B A    的路径匀速移动，设点 P 经过的路径长是 x ， APD 的面积是 y ，则下列图像能大致反 映 y 与 x 之间的函数关系的是( ) 8.某市储运部紧急调拨一批物资，调进物资共用 4h，调进物资 2h 后开始调出物资(调进物资 与调出物资的速度探持不变).储运部库存物资 S (t)与时间t (h)之间的函数关系如图所示， 这批物资从开始调进到全部调出需要的时间是( ) A. 4 h B. 4.4 h C. 4.8 h D. 5 h 二、填空题 9.在函数 1 2y x   中，自变量 x 的取值范围是 . 10.设点 ( 1, )m 和点 1( , )2 n 是直线 2( 1)y k x b   ( 0 1k  )上的两个点，则 ,m n 的大小 关系是 . 11. 若点 ( , )A m n 在直线 ( 0)y kx k  上，当 1 1m   时， 1 1n   ，则这条直线的函 数表达式是 . 12.若直线l 经过点 (1,0)A ，且与直线 y x 垂直，则直线l 的函数表达式是 . 13.在平面直角坐标系中，有 ( 1,0)A  ， (3,0)B ， (0, 1)C  三点， (1, )D m 是一个动点.当 ACD 的周长最小时， ABD 的面积是 . 14.如图， , , ,A B C D 是平面直角坐标系中坐标轴上的点，且 AOB COD   .设直线 AB 的 表达式为 1 1 1y k x b  ，直线CD 的表达式为 2 2 2y k x b  ，则 1 2k k g . 第 3页（共 8页） 15.如图，在平面直角坐标系中，函数 2y x 和 y x  的图像分别为直线 1 2,l l ，若过点 (1,0) 作 x 轴的垂线交 1l 于点 1A ，过点 1A 作 y 轴的垂线交 2l 于点 2A ，过点 2A 作 x 轴的垂线交 1l 于点 3A ，过点 3A 作 y 轴的垂线交 2l 于点 4A ，…，依次进行下去，则点 2018A 的坐标 是 . 16.小敏从 A 地出发向 B 地行走，同时小聪从 B 地出发向 A 地行走，如图所示，相交于点 P 的两条线段 1 2,l l 分别表示小敏、小聪离 B 地的距离 y (km)与已用时间 x (h)之间的关系， 则 x  时，小敏、小聪两人相距 7 km. 17. ,A B 两地之间的路程为 2 380 m，甲、乙两人分别从 ,A B 两地出发，相向而行.已知甲 先出发 5 min 后，乙才出发，他们两人在 ,A B 之间的 C 地相遇，相遇后，甲立即返回 A 地，乙继续向 A 地前行.甲到达 A 地时停止行走，乙到达 A 地时也停止行走，在整个行 走过程中，甲、乙两人均保持各自的速度匀速行走，甲、乙两人相距的路程 y (m)与甲 出发的时间 x (min)之间的关系如图所示，则乙到达 A 地时，甲与 A 地相距的路程是 m. 18.已知一次函数 y y mx n  的图像如图所示，则代数式 m n m n   化简后的结果 是 . 三、解答题 19. (6 分)已知 3y  与 2x  成正比例，且当 3x  时， 7y  . (1)写出 y 与 x 之间的函数表达式; (2)当 1x   时，求 y 的值; 第 4页（共 8页） (3)若 y 的取值范围为 11 2y   ，求 x 的取值范围. 20. ( 6 分)如图，一次函数 2 3y mx m   的图像与 1 2y x  的图像交于点C ，与 x 轴和 y 轴分别交于点 A 和点 B ，且点C 的横坐标为 3 . (1)求 m 的值与 AB 的长; (2)若点Q 为线段OB 上一点，且 1 4OCQ BAOS S  ，求点Q 的坐标. 21. (6 分)某市为节约水资源，制定了新的居民用水收费标准，按照新标准，用户每月缴纳的 水费 y (元)与每月用水量 x (m3)之间的关系如图所示. (1)求 y 关于 x 的函数表达式; (2)若某用户二、三月份共用水 40 m3(二月份用水量不超过 25 m3)，共缴纳水费 79.8 元， 则该用户二、三月份的用水量各是多少? 22. ( 6 分)如图，函数 1 2y x b   的图像与 x 轴， y 轴分别交于点 ,A B ，与函数 y x 的 图像交于点 M ，点 M 的横坐标为 2.在 x 轴上有一点 ( ,0)P a (其中 2a  )，过点 P 作 x 轴 的垂线，分别交函数 1 2y x b   和 y x 的图像于点 ,C D . (1)求点 A 的坐标; (2)若OB CD ，求 a 的值. 第 5页（共 8页） 23. ( 8 分)小明家今年种植的“红灯” 樱桃喜获丰收，采摘上市 20 天全部销售完.小明对销 售情况进行跟踪记录，并将记录情况绘成图像，日销售量 y (kg)与上市时间 x (天)的函数 关系如图①所示，樱桃价格 z (元/kg)与上市时间 x (天)的函数关系如图②所示. (1)观察图像，直接写出日销售量的最大值; (2)求小明家樱桃的日销售量 y 与上市时间 x 的函数表达式; (3)第 10 天与第 12 天的销售金额哪天多? 24. ( 8 分)如图，点 ,A B 分别是 x 轴上位于原点两侧的两点，点 (2, )P p 在第一象限，直线 PA 交 y 轴于点 (0,2)C ，直线 PB 交 y 轴于点 D ， 6AOPS  . (1)求 COPS ; (2)求点 A 的坐标及 p 的值; (3)若 AOP BOPS S  ，求直线 BD 的函数表达式. 第 6页（共 8页） 25. ( 8 分)某客运公司有豪华和普通两种客车在甲、乙两市之间运营.已知每隔 1h 有一辆豪华 客车从甲城开往乙城，如图所示，OA 是第一辆豪华客车离开甲市的路程 s (km)与运行时 间t (h)的函数图像， BC 是一辆从乙市开往甲市的普通客车距甲市的路程 s (km)与运行时 间t (h)的函数图像.请根据图中提供的信息，解答下列问题: (1)点 B 的横坐标 0.5 的意义是普通客车发车时间比第一辆豪华客车发车时间 ，点 B 的纵坐标 480 的意义是 . (2)请你在原图中直接画出第二辆豪华客车离开甲市的路程 s (km)与运行时间 t (h)的函数 图像; (3)若普通客车的速度为 80 km/h. ①求 BC 的函数表达式，并写出自变量t 的取值范围; ②求第二辆豪华客车出发后多长时间与普通客车相遇; ③写出这辆普通客车在行驶途中与迎面而来的相邻两辆豪华客车相遇的间隔时间. 26. ( 8 分)操作:“如图①，P 是平面直角坐标系中的一点( x 轴上的点除外)，过点 P 作 PC x 轴于点C ，点C 绕点 P 逆时针旋转 60º得到点Q .”我们将此由点 P 得到点 Q 的操作称为 点的T 变换. (1) 点 ( , )P a b 经 过 T 变 换 后 得 到 的 点 Q 的 坐 标 为 ; 若 点 M 经 过 T 变 换 后 得 到 点 (6, 3)N  ，则点 M 的坐标为 ; (2) A 是函数 3 2y x 图像上异于原点O 的任意一点，经过T 变换后得到点 B . ①求经过 ,O B 两点的直线的函数表达式; ②如图②，直线 AB 交 y 轴于点 D ，求 OAB 的面积与 OAD 的面积之比. 第 7页（共 8页） 参考答案 1-8 CDDAADBB 9. 2x   10. m n 11. y x 或 y x  12. 1y x   13. 4 3 14. 1 15. 1009 1009( 2 ,2 ) 16. 0.6 或 2.6 17. 180 18. 2n 19. (1) 2 1y x  (2) 1y   (3) 11 4x    20. (1) 3 2m  2 13AB  (2) (0,2)Q 21. (1) y  1.8 (0 15) 2.4 9( 15) x x x x      (2) 二三月份的用水量分别是 12m3 和 28m3 22. (1) (6,0)A (2) 4a  23. (1) 最大值为 120kg (2) y  10 (0 12) 15 300(12 20) x x x x       (3)第 10 天的销售金额多 24. (1) 三角形的面积为 2 (2) ( 4,0)A  3p  (3) 3 62BDy x   25. (1) 晚 0.5h 甲乙两市相距 480km (2) 函数图像为图中的线段 MN 第 8页（共 8页） (3) ① 80 520(0.5 6.5)s t t     ②第二辆客车出发 2.2h 后与普通客车相遇 ③间隔时间为 0.6h 26. (1) 3( , )2 2 ba b (9, 2 3) (2) ① 3 7y x ②面积之比为 3:4