2019-2020学年广东省潮州市潮安区八年级（下）期中数学试卷 解析版 20页

2019-2020 学年广东省潮州市潮安区八年级（下）期中数学试卷 一、选择题：本大题共 10 小题，每小题 3 分，共 30 分. 1．（3 分）4 的算术平方根是（ ） A．±2 B．2 C．﹣2 D． 2．（3 分）在下列给出的条件中，能判定四边形 ABCD 为平行四边形的是（ ） A．AB∥CD，AD＝BC B．∠A＝∠B，∠C＝∠D C．AB∥CD，AB＝CD D．AB＝AD，CB＝CD 3．（3 分）下列各组数中，以 a，b，c 为边的三角形不是直角三角形的是（ ） A．a＝1.5，b＝2，c＝3 B．a＝7，b＝24，c＝25 C．a＝6，b＝8，c＝10 D．a＝5，b＝12，c＝13 4．（3 分）下列计算正确的是（ ） A． B． C． D． 5．（3 分）下列命题中，其逆命题成立的是（ ） A．如果 a、b 都是正数，那么它们的积也是正数 B．如果 ＝ ，那么 a＝b C．菱形的对角线互相垂直 D．平行四边形的对角线互相平分 6．（3 分）如图，在菱形 ABCD 中，AB＝5，∠B：∠BCD＝1：2，则对角线 AC 等于（ ） A．5 B．10 C．15 D．20 7．（3 分）若 有意义，则 x 满足条件（ ） A．x＞2． B．x≥2 C．x＜2 D．x≤2． 8．（3 分）若直角三角形的两条直角边长分别为 3cm、4cm，则该直角三角形斜边上的高为（ ） A． cm B． cm C．5 cm D． cm 9．（3 分）如图，在 Rt△ABC 中，∠ACB＝90°，点 D，E 分别是边 AB，AC 的中点，延长 BC 至 F， 使 CF＝ BC，若 AB＝10，则 EF 的长是（ ） A．5 B．4 C．3 D．2 10．（3 分）如图，已知圆柱底面的周长为 4，圆柱的高为 2，在圆柱的侧面上，过点 A 和点 C 有一圈 金属丝，则这圈金属丝的周长的最小值为（ ） A． B． C． D． 二、填空题：本大题共 7 小题，每小题 4 分，共 28 分．请将下列各题的正确答案填写在横线上． 11．（4 分）计算： ＝ ． 12．（4 分）若 x＝ ，则 x2+2x+1＝ ． 13．（4 分）如图，数轴上点 A 表示的实数是 ． 14．（4 分）矩形的两条对角线的夹角为 60°，较短的边长为 12cm，则对角线长为 cm． 15．（4 分）如图，已知在 Rt△ABC 中，∠ACB＝90°，AB＝4，分别以 AC、BC 为直径作半圆，面积 分别记为 S1、S2，则 S1+S2 等于 ． 16．（4 分）如图，菱形 ABCD 的边长为 2，∠DAB＝60°，点 E 为 BC 边的中点，点 P 为对角线 AC 上一动点，则 PB+PE 的最小值为 ． 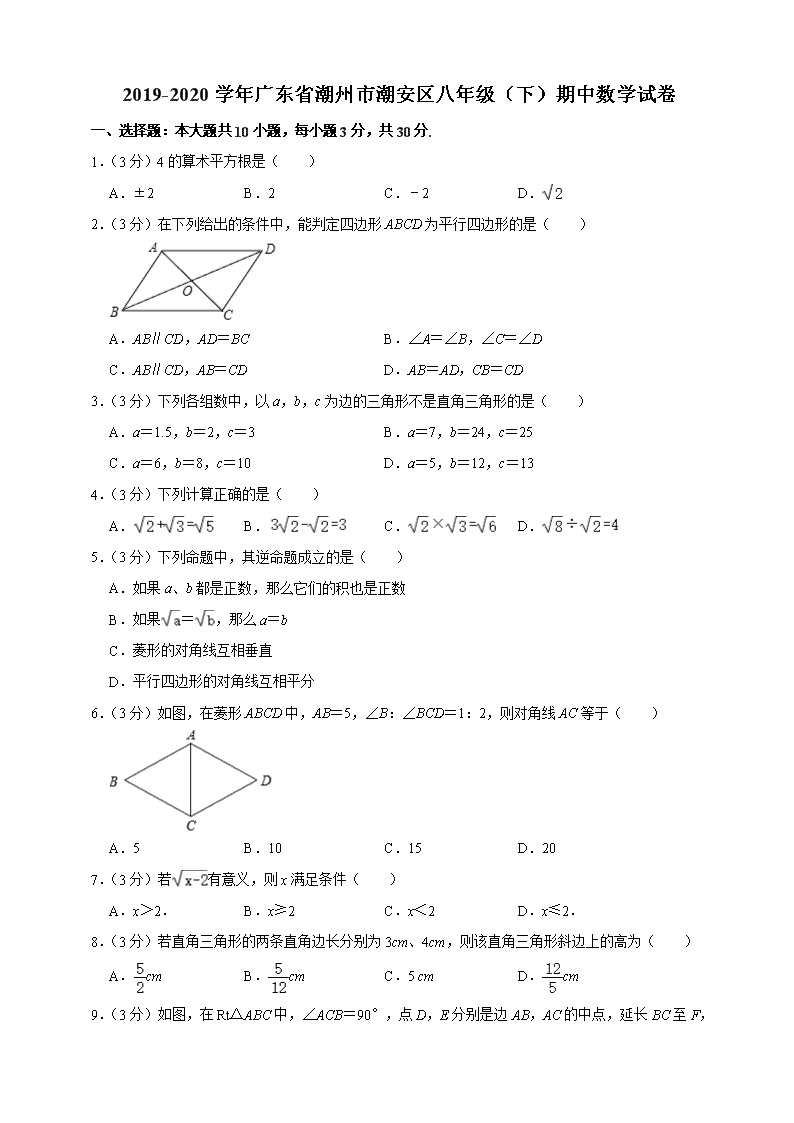17．（4 分）如图，在 Rt△ABC 中，∠ACB＝90°，AB＝5cm，AC＝3cm，动点 P 从点 B 出发沿射线 BC 以 1cm/s 的速度移动，设运动的时间为 t 秒，当△ABP 为等腰三角形时，t 的取值为 ． 三、解答题（一）：本大题共 3 小题，每小题 6 分，共 18 分 18．（6 分）计算： ． 19．（6 分）已知 a＝2+ ，b＝2﹣ ，求 a2+2ab+b2 的值． 20．（6 分）如图，△ABC 中，∠A＝90°，∠C＝30°，AB＝4，BD＝5，求 AD 和 BC 的长． 四、解答题（二）：本大题共 3 小题，每小题 8 分，共 24 分 21．（8 分）已知 a、b、c 满足 ． （1）求 a、b、c 的值； （2）判断以 a、b、c 为边的三角形的形状． 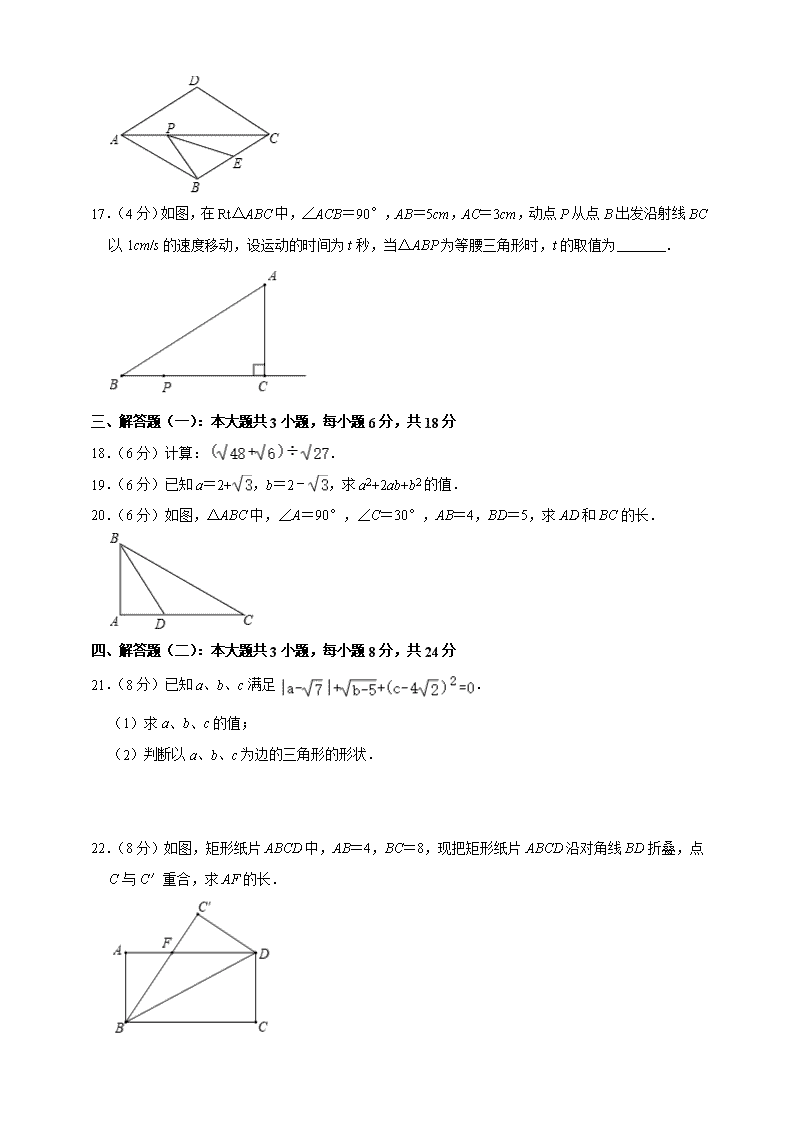22．（8 分）如图，矩形纸片 ABCD 中，AB＝4，BC＝8，现把矩形纸片 ABCD 沿对角线 BD 折叠，点 C 与 C′重合，求 AF 的长． 23．（8 分）如图，在△ABC 中，∠BAC＝90°，AD 是中线，E 是 AD 的中点，过点 A 作 AF∥BC 交 BE 的延长线于 F，连接 CF． （1）求证：AD＝AF； （2）如果 AB＝AC，试判断四边形 ADCF 的形状，并证明你的结论． 五、解答题（三）：本大题共 2 小题，每小题 10 分，共 20 分. 24．（10 分）如图 1，四边形 ABCD 是正方形，点 E、K 分别在 BC、AB 上，点 G 在 BA 的延长线上， 且 CE＝BK＝AG． （1）求证： ① DE＝DG； ② DE⊥DG； （2）以线段 DE、DG 为边作出正方形 DEFG，连接 KF，猜想并写出四边形 CEFK 是怎样的特殊 四边形，并证明你的猜想． 25．（10 分）如图，菱形 ABCD 中，AB＝6cm，∠ADC＝60°，点 E 从点 D 出发，以 1cm/s 的速度沿 射线 DA 运动，同时点 F 从点 A 出发，以 1cm/s 的速度沿射线 AB 运动，连接 CE、CF 和 EF，设运 动时间为 t（s）． （1）当 t＝3s 时，连接 AC 与 EF 交于点 G，如图 ① 所示，则 EF＝ cm； （2）当 E、F 分别在线段 AD 和 AB 上时，如图 ② 所示，求证：△CEF 是等边三角形； （3）在（2）的条件下，连接 BD 交 CE 于点 G，若 BG＝BC，求 EF 的长和此时的 t 值． 2019-2020 学年广东省潮州市潮安区八年级（下）期中数学试卷 参考答案与试题解析 一、选择题：本大题共 10 小题，每小题 3 分，共 30 分. 1．（3 分）4 的算术平方根是（ ） A．±2 B．2 C．﹣2 D． 【分析】根据开方运算，可得一个数的算术平方根． 【解答】解：4 的算术平方根是 2， 故选：B． 2．（3 分）在下列给出的条件中，能判定四边形 ABCD 为平行四边形的是（ ） A．AB∥CD，AD＝BC B．∠A＝∠B，∠C＝∠D C．AB∥CD，AB＝CD D．AB＝AD，CB＝CD 【分析】根据平行四边形的判定方法即可得出结论． 【解答】解：A、由 AB∥CD，AD＝BC 不能判定四边形 ABCD 为平行四边形； B、由∠A＝∠B，∠C＝∠D 不能判定四边形 ABCD 为平行四边形； C、由 AB∥CD，AB＝CD 能判定四边形 ABCD 为平行四边形； D、AB＝AD，BC＝CD 不能判定四边形 ABCD 为平行四边形； 故选：C． 3．（3 分）下列各组数中，以 a，b，c 为边的三角形不是直角三角形的是（ ） A．a＝1.5，b＝2，c＝3 B．a＝7，b＝24，c＝25 C．a＝6，b＝8，c＝10 D．a＝5，b＝12，c＝13 【分析】由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可． 【解答】解：A、1.52+22≠32，故不是直角三角形，故此选项符合题意； B、72+242＝252，故是直角三角形，故此选项不合题意； C、62+82＝102，故是直角三角形，故此选项不合题意； D、52+122＝132，故是直角三角形，故此选项不合题意． 故选：A． 4．（3 分）下列计算正确的是（ ） A． B． C． D． 【分析】根据二次根式的运算法则即可求出答案． 【解答】解：（A） 与 不是同类二次根式，故不能合并，故 A 错误． （B）原式＝2 ，故 B 错误． （D）原式＝2，故 D 错误． 故选：C． 5．（3 分）下列命题中，其逆命题成立的是（ ） A．如果 a、b 都是正数，那么它们的积也是正数 B．如果 ＝ ，那么 a＝b C．菱形的对角线互相垂直 D．平行四边形的对角线互相平分 【分析】根据逆命题的概念得出原命题的逆命题，判断即可 【解答】解：A、逆命题不成立，两个负数的乘积是正数．本选项不符合题意． B、逆命题不成立，两个相等负数没有平方根．本选项不符合题意． C、逆命题不成立，对角线垂直的四边形不一定是菱形．本选项不符合题意． D、逆命题成立．本选项符合题意． 故选：D． 6．（3 分）如图，在菱形 ABCD 中，AB＝5，∠B：∠BCD＝1：2，则对角线 AC 等于（ ） A．5 B．10 C．15 D．20 【分析】根据题意可得出∠B＝60°，结合菱形的性质可得 BA＝BC，判断出△ABC 是等边三角形 即可得到 AC 的长． 【解答】解：∵四边形 ABCD 是菱形， ∴∠B+∠BCD＝180°，AB＝BC， ∵∠B：∠BCD＝1：2， ∴∠B＝60°， ∴△ABC 是等边三角形， ∴AB＝BC＝AC＝5． 故选：A． 7．（3 分）若 有意义，则 x 满足条件（ ） A．x＞2． B．x≥2 C．x＜2 D．x≤2． 【分析】根据二次根式中的被开方数必须是非负数，即可得到关于 x 的不等式组，即可求解． 【解答】解：根据题意得：x﹣2≥0， 解得：x≥2． 故选：B． 8．（3 分）若直角三角形的两条直角边长分别为 3cm、4cm，则该直角三角形斜边上的高为（ ） A． cm B． cm C．5 cm D． cm 【分析】先根据勾股定理求出斜边的长度，再根据三角形的面积列式进行计算即可求解． 【解答】解：根据勾股定理，斜边＝ ＝5， 设斜边上的高为 h， 则 S△＝ ×3×4＝ ×5•h， 整理得 5h＝12， 解得 h＝ cm． 故选：D． 9．（3 分）如图，在 Rt△ABC 中，∠ACB＝90°，点 D，E 分别是边 AB，AC 的中点，延长 BC 至 F， 使 CF＝ BC，若 AB＝10，则 EF 的长是（ ） A．5 B．4 C．3 D．2 【分析】由三角形中位线定理得出 DE∥BC，由直角三角形斜边上的中线性质得出 CD＝ AB＝AD ＝BD，又 CF＝ BC，即可证出四边形 CDEF 是平行四边形，由此即可解决问题． 【解答】解：∵AD＝DB，AE＝EC， ∴DE∥BC，DE＝ BC， ∵CF＝ BC， ∴DF∥CF，DF＝CF， ∴四边形 DEFC 是平行四边形， ∴EF＝CD， ∵∠ACB＝90°，AD＝DB，AB＝10， ∴CD＝ AB＝5， ∴EF＝5． 故选：A． 10．（3 分）如图，已知圆柱底面的周长为 4，圆柱的高为 2，在圆柱的侧面上，过点 A 和点 C 有一圈 金属丝，则这圈金属丝的周长的最小值为（ ） A． B． C． D． 【分析】要求丝线的长，需将圆柱的侧面展开，进而根据“两点之间线段最短”得出结果，在求线 段长时，根据勾股定理计算即可． 【解答】解：如图，把圆柱的侧面展开，得到矩形，则这圈金属丝的周长最小为 2AC 的长度． ∵圆柱底面的周长为 4，圆柱高为 2， ∴AB＝2dm，BC＝BC′＝2， ∴AC2＝22+22＝4+4＝8， ∴AC＝2 ， ∴这圈金属丝的周长最小为 2AC＝4 ． 故选：D． 二、填空题：本大题共 7 小题，每小题 4 分，共 28 分．请将下列各题的正确答案填写在横线上． 11．（4 分）计算： ＝ 18 ． 【分析】根据二次根式乘法、积的乘方法则解答． 【解答】解：原式＝（3 ）2＝9×2＝18． 12．（4 分）若 x＝ ，则 x2+2x+1＝ 5 ． 【分析】先利用完全平方公式得到 x2+2x+1＝（x+1）2，然后把 x 的值代入计算即可． 【解答】解：∵x＝ ， ∴x2+2x+1＝（x+1）2 ＝（ ﹣1+1）2 ＝5． 故答案为 5． 13．（4 分）如图，数轴上点 A 表示的实数是 ﹣1 ． 【分析】直接利用勾股定理得出三角形斜边长即可得出 A 点对应的实数． 【解答】解：由图形可得：﹣1 到 A 的距离为 ＝ ， 则数轴上点 A 表示的实数是： ﹣1． 故答案为： ﹣1． 14．（4 分）矩形的两条对角线的夹角为 60°，较短的边长为 12cm，则对角线长为 24 cm． 【分析】根据矩形对角线相等且互相平分性质和题中条件易得△AOB 为等边三角形，即可得到矩形 对角线一半长，进而求解即可． 【解答】解：如图：AB＝12cm，∠AOB＝60°． ∵四边形是矩形，AC，BD 是对角线． ∴OA＝OB＝OD＝OC＝ BD＝ AC． 在△AOB 中，OA＝OB，∠AOB＝60°． ∴OA＝OB＝AB＝12cm，BD＝2OB＝2×12＝24cm． 故答案为：24． 15．（4 分）如图，已知在 Rt△ABC 中，∠ACB＝90°，AB＝4，分别以 AC、BC 为直径作半圆，面积 分别记为 S1、S2，则 S1+S2 等于 2 π ． 【分析】根据半圆面积公式结合勾股定理，知 S1+S2 等于以斜边为直径的半圆面积． 【解答】解：S1＝ π （ ）2＝ π AC2，S2＝ π BC2， 所以 S1+S2＝ π （AC2+BC2）＝ π AB2＝2 π ． 故答案为：2 π ． 16．（4 分）如图，菱形 ABCD 的边长为 2，∠DAB＝60°，点 E 为 BC 边的中点，点 P 为对角线 AC 上一动点，则 PB+PE 的最小值为 ． 【分析】找出 B 点关于 AC 的对称点 D，连接 DE 交 AC 于 P，则 DE 就是 PB+PE 的最小值，求出 即可． 【解答】解：连接 BD，交 AC 于 O，连接 DE 交 AC 于 P， 由菱形的对角线互相垂直平分，可得 B、D 关于 AC 对称，则 PD＝PB， ∴PE+PB＝PE+PD＝DE， 即 DE 就是 PE+PB 的最小值． ∵四边形 ABCD 是菱形， ∴∠DCB＝∠DAB＝60°，DC＝BC＝2， ∴△DCB 是等边三角形， ∵BE＝CE＝1， ∴DE⊥AB（等腰三角形三线合一的性质）． 在 Rt△ADE 中，DE＝ ＝ ． 即 PB+PE 的最小值为 ． 故答案为 ． 17．（4 分）如图，在 Rt△ABC 中，∠ACB＝90°，AB＝5cm，AC＝3cm，动点 P 从点 B 出发沿射线 BC 以 1cm/s 的速度移动，设运动的时间为 t 秒，当△ABP 为等腰三角形时，t 的取值为 5 或 t＝8 或 t＝ ． 【分析】当△ABP 为等腰三角形时，分三种情况： ① 当 AB＝BP 时； ② 当 AB＝AP 时； ③ 当 BP ＝AP 时，分别求出 BP 的长度，继而可求得 t 值． 【 解 答 】 解 ： 在 Rt △ ABC 中 ， BC2 ＝ AB2 ﹣ AC2 ＝ 52 ﹣ 32 ＝ 16 ， ∴BC＝4（cm）； ① 当 AB＝BP 时，如图 1，t＝5； ② 当 AB＝AP 时，如图 2，BP＝2BC＝8cm，t＝8； ③ 当 BP＝AP 时，如图 3，AP＝BP＝tcm，CP＝（4﹣t）cm，AC＝3cm， 在 Rt△ACP 中，AP2＝AC2+CP2， 所以 t2＝32+（4﹣t）2， 解得：t＝ ， 综上所述：当△ABP 为等腰三角形时，t＝5 或 t＝8 或 t＝ ． 故答案为：5 或 t＝8 或 t＝ ． 三、解答题（一）：本大题共 3 小题，每小题 6 分，共 18 分 18．（6 分）计算： ． 【分析】先把二次根式化为最简二次根式，然后利用二次根式的除法法则运算． 【解答】解：原式＝（4 + ）÷3 ＝ + ． 19．（6 分）已知 a＝2+ ，b＝2﹣ ，求 a2+2ab+b2 的值． 【分析】先计算出 a+b，则利用完全平方公式得到 a2+2ab+b2＝（a+b）2，然后利用整体代入的方 法计算． 【解答】解：∵a＝2+ ，b＝2﹣ ， ∴a+b＝4， ∴a2+2ab+b2＝（a+b）2＝42＝16． 20．（6 分）如图，△ABC 中，∠A＝90°，∠C＝30°，AB＝4，BD＝5，求 AD 和 BC 的长． 【分析】根据勾股定理解答即可． 【解答】解：∵△ABC 中，∠A＝90°，∠C＝30°，AB＝4，BD＝5， ∴ ＝ ＝3， ∵∠A＝90°，∠C＝30°，AB＝4 ∴BC＝2AB＝2×4＝8． 四、解答题（二）：本大题共 3 小题，每小题 8 分，共 24 分 21．（8 分）已知 a、b、c 满足 ． （1）求 a、b、c 的值； （2）判断以 a、b、c 为边的三角形的形状． 【分析】（1）根据非负数的性质可求出 a、b、c 的值； （2）利用勾股定理的逆定理证明三角形是直角三角形． 【解答】解：（1）根据题意得：a﹣ ＝0，b﹣5＝0，c﹣4 ＝0， 解得：a＝ ，b＝5，c＝4 ； （2）∵（ ）2+52＝（4 ）2， ∴a2+b2＝c2， ∴以 a、b、c 为边的三角形是直角三角形． 22．（8 分）如图，矩形纸片 ABCD 中，AB＝4，BC＝8，现把矩形纸片 ABCD 沿对角线 BD 折叠，点 C 与 C′重合，求 AF 的长． 【分析】由矩形的性质可得，AB﹣CD＝4，BC＝AD＝8，∠A＝∠ABC＝∠C＝∠CDA＝90°，由 折叠得：CD＝C′D＝4，BC＝BC′＝8，∠CBD＝∠C′BD，进而得到 FB＝FD，设未知数，将问 题转化到直角三角形 ABF 中，由勾股定理建立方程求解即可． 【解答】解：∵ABCD 是矩形， ∴AB﹣CD＝4，BC＝AD＝8，∠A＝∠ABC＝∠C＝∠CDA＝90°， 由折叠得：CD＝C′D＝4，BC＝BC′＝8，∠CBD＝∠C′BD， ∵∠CBD＝∠ADB， ∴∠ADB＝∠C′BD， ∴FB＝FD， 设 AF＝x，则 FC′＝x，FB＝FD＝8﹣x， 在 Rt△ABF 中，由勾股定理得， 42+x2＝（8﹣x）2， 解得，x＝3，即 AF＝3． 答：AF 的长为 3． 23．（8 分）如图，在△ABC 中，∠BAC＝90°，AD 是中线，E 是 AD 的中点，过点 A 作 AF∥BC 交 BE 的延长线于 F，连接 CF． （1）求证：AD＝AF； （2）如果 AB＝AC，试判断四边形 ADCF 的形状，并证明你的结论． 【分析】（1）由 E 是 AD 的中点，AF∥BC，易证得△AEF≌△DEB，即可得 AF＝BD，又由在△ABC 中，∠BAC＝90°，AD 是中线，根据直角三角形斜边的中线等于斜边的一半，即可证得 AD＝BD ＝CD＝ BC，即可证得：AD＝AF； （2）由 AF＝BD＝DC，AF∥BC，可证得：四边形 ADCF 是平行四边形，又由 AB＝AC，根据三线 合一的性质，可得 AD⊥BC，AD＝DC，继而可得四边形 ADCF 是正方形． 【解答】（1）证明：∵AF∥BC， ∴∠EAF＝∠EDB， ∵E 是 AD 的中点， ∴AE＝DE， 在△AEF 和△DEB 中， ， ∴△AEF≌△DEB（ASA）， ∴AF＝BD， ∵在△ABC 中，∠BAC＝90°，AD 是中线， ∴AD＝BD＝DC＝ BC， ∴AD＝AF； （2）解：四边形 ADCF 是正方形． ∵AF＝BD＝DC，AF∥BC， ∴四边形 ADCF 是平行四边形， ∵AB＝AC，AD 是中线， ∴AD⊥BC， 又∵AD＝AF， ∴四边形 ADCF 是正方形． 五、解答题（三）：本大题共 2 小题，每小题 10 分，共 20 分. 24．（10 分）如图 1，四边形 ABCD 是正方形，点 E、K 分别在 BC、AB 上，点 G 在 BA 的延长线上， 且 CE＝BK＝AG． （1）求证： ① DE＝DG； ② DE⊥DG； （2）以线段 DE、DG 为边作出正方形 DEFG，连接 KF，猜想并写出四边形 CEFK 是怎样的特殊 四边形，并证明你的猜想． 【分析】（1） ① 根据正方形性质求出 AD＝DC，∠GAD＝∠DCE＝90°，根据全等三角形判定推 出即可； ② 根据全等得出∠GDA＝∠CDE，求出∠GDE＝∠GDA+∠ADE＝∠ADC＝90°即可； （2）四边形 CEFK 是平行四边形，推出 EF＝CK，EF∥CK，根据平行四边形的判定推出即可． 【解答】（1） ① 证明：∵四边形 ABCD 是正方形， ∴AD＝DC，∠GAD＝∠DCE＝90°， 在△GAD 和△ECD 中 ∴△GAD≌△ECD（SAS）， ∴DE＝DG； ② ∵四边形 ABCD 是正方形， ∴∠ADC＝90°， ∵△GAD≌△ECD， ∴∠GDA＝∠CDE， ∴∠GDE＝∠GDA+∠ADE＝∠CDE+∠ADE＝∠ADC＝90°， ∴DE⊥DG； （2）四边形 CEFK 是平行四边形，理由如下： 证明：∵四边形 ABCD 是正方形， ∴∠B＝∠ECD＝90°，BC＝CD， 在△KBC 和△ECD 中 ， ∴△KBC≌△ECD（SAS）， ∴DE＝CK，∠DEC＝∠BKC， ∵∠B＝90°， ∴∠KCB+∠BKC＝90°， ∴∠KCB+∠DEC＝90°， ∴∠EOC＝180°﹣90°＝90°， ∵四边形 DGFE 是正方形， ∴DE＝EF＝CK，∠FED＝90°＝∠EOC， ∴CK∥EF， ∴四边形 CEFK 是平行四边形． 25．（10 分）如图，菱形 ABCD 中，AB＝6cm，∠ADC＝60°，点 E 从点 D 出发，以 1cm/s 的速度沿 射线 DA 运动，同时点 F 从点 A 出发，以 1cm/s 的速度沿射线 AB 运动，连接 CE、CF 和 EF，设运 动时间为 t（s）． （1）当 t＝3s 时，连接 AC 与 EF 交于点 G，如图 ① 所示，则 EF＝ 3 cm； （2）当 E、F 分别在线段 AD 和 AB 上时，如图 ② 所示，求证：△CEF 是等边三角形； （3）在（2）的条件下，连接 BD 交 CE 于点 G，若 BG＝BC，求 EF 的长和此时的 t 值． 【分析】（1）易证△ABC 是等边三角形，当 t＝3s 时，AF＝DE＝3，则 BF＝AE＝3＝AF，由等腰 三角形的性质得出 AG⊥EF，GF＝GE，推出∠AFE＝∠AEF＝30°，由含 30°角直角三角形的性 质得 AG＝ AF＝ ，由勾股定理得 GF＝ AG＝ ，即可得出结果； （2）连接 AC，则△ADC 和△ABC 是等边三角形，由 SAS 证得△DCE≌△ACF，得出 CE＝CF， ∠DCE＝∠ACF，再证∠ECF＝60°，即可得出结论； （3）连接 AC 交 BD 于 O，过点 E 作 EN⊥CD 于 N，由菱形的性质与∠ADC＝60°，得出 AD∥BC， ∠BCD＝120°，DA＝DC＝AB＝BC＝6，BO＝DO，∠CBO＝ ∠ABC＝ ∠ADC＝30°，AC⊥BD， 求出 OC＝ BC＝3，BO＝ ＝3 ，BD＝2BO＝6 ，DG＝BD﹣BG＝6 ﹣6，由等 腰三角形的性质求出∠BGC＝∠BCG＝75°，证∠DEG＝∠DGE，得出 DE＝DG＝6 ﹣6，则 t ＝（6 ﹣6）s，易求∠DCE＝45°，DN＝ DE＝3 ﹣3，EN＝ ＝9﹣3 ，再证明 △ENC 是等腰直角三角形，得 CE＝ EN＝9 ﹣3 ，即可得出结果． 【解答】（1）解：∵四边形 ABCD 是菱形， ∴DA＝DC＝AB＝BC＝6，∠ADC＝∠ABC＝60°，∠BAC＝∠DAC，AD∥BC， ∴∠BAD＝180°﹣∠ABC＝120°，∠BAC＝60°， ∴△ABC 是等边三角形， 当 t＝3s 时，AF＝DE＝3， ∴BF＝AE＝3＝AF， ∵∠BAC＝∠DAC＝60°， ∴AG⊥EF，GF＝GE， ∴∠AFE＝∠AEF＝30°， ∴AG＝ AF＝ ，GF＝ AG＝ ， ∴EF＝2GF＝3 ， 故答案为：3 ； （2）证明：∵四边形 ABCD 是菱形， ∴DA＝DC＝AB＝BC，∠ADC＝∠ABC＝60°， 连接 AC，如图 ② 所示： 则△ADC 和△ABC 是等边三角形， ∴∠D＝∠ACD＝∠CAF＝60°，DC＝AC， ∵点 E 从点 D 出发，以 1cm/s 的速度沿射线 DA 运动，同时点 F 从点 A 出发，以 1cm/s 的速度沿射 线 AB 运动， ∴DE＝AF， 在△DCE 和△ACF 中， ， ∴△DCE≌△ACF（SAS）， ∴CE＝CF，∠DCE＝∠ACF， ∵∠ACD＝∠DCE+∠ACE＝60°， ∴∠DCE+∠ACE＝∠ACF+∠ACE＝∠ECF＝60°， ∴△CEF 是等边三角形； （3）解：连接 AC 交 BD 于 O，过点 E 作 EN⊥CD 于 N，如图 ② ﹣1 所示： ∵四边形 ABCD 是菱形，∠ADC＝60°， ∴AD∥BC，∠BCD＝120°，DA＝DC＝AB＝BC＝6，BO＝DO，∠CBO＝ ∠ABC＝ ∠ADC＝ 30°，AC⊥BD， ∴在 Rt△BOC 中，OC＝ BC＝ ×6＝3， 由勾股定理得：BO＝ ＝ ＝3 ， ∴BD＝2BO＝6 ， ∵BG＝BC＝6， ∴DG＝BD﹣BG＝6 ﹣6， ∵BG＝BC， ∴∠BGC＝∠BCG＝ （180°﹣∠CBO）＝ （180°﹣30°）＝75°， ∵∠BGC＝∠DGE， ∴∠BCG＝∠DGE， ∵AD∥BC， ∴∠DEG＝∠BCG， ∴∠DEG＝∠DGE， ∴DE＝DG＝6 ﹣6， ∴t＝（6 ﹣6）s， ∵∠BCD＝120°， ∴∠DCE＝∠BCD﹣∠BCG＝120°﹣75°＝45°， 在 Rt△DNE 中，∠ADC＝60°， ∴∠DEN＝30°， ∴DN＝ DE＝ ×（6 ﹣6）＝3 ﹣3， 由勾股定理得：EN＝ ＝ ＝9﹣3 ， ∵∠DCE＝45°， ∴△ENC 是等腰直角三角形， ∴CE＝ EN＝ ×（9﹣3 ）＝9 ﹣3 ， ∵△CEF 是等边三角形， ∴EF＝CE＝（9 ﹣3 ）cm．