2020八年级数学上册 第4章 一次函数 第4节 一次函数的应用教案 （新版）北师大版 5页

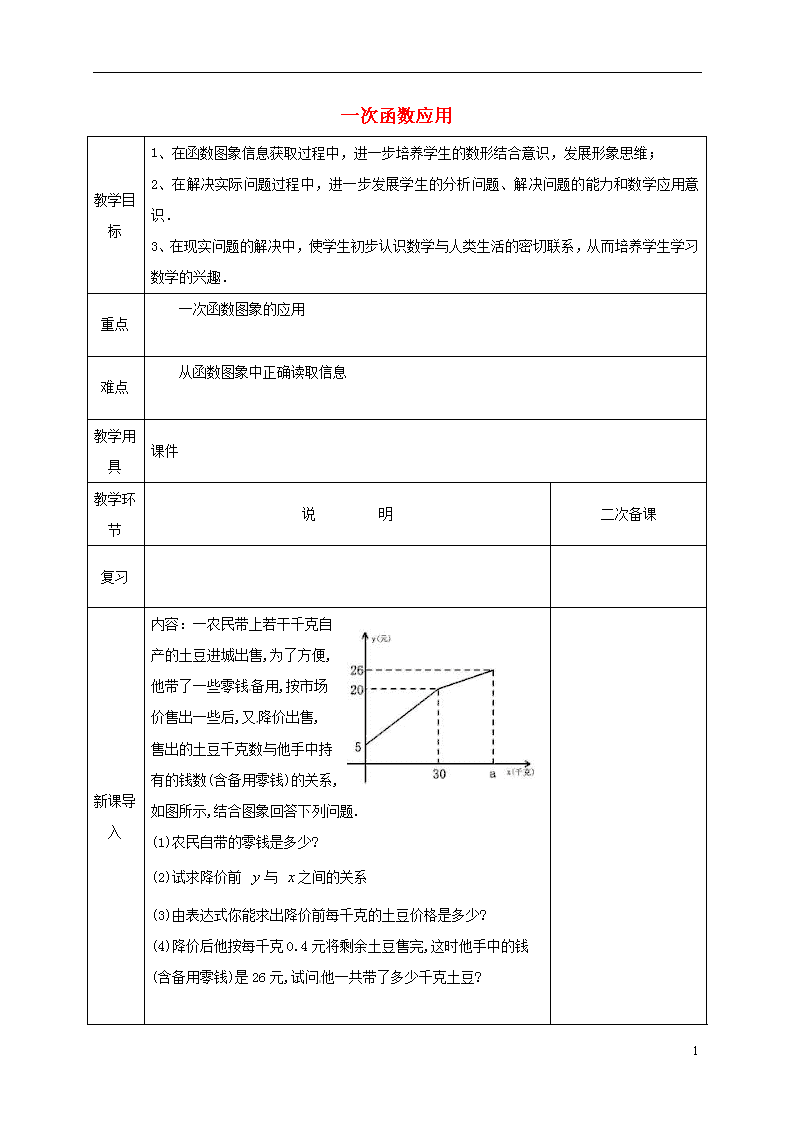
一次函数应用 教学目标 ‎1、在函数图象信息获取过程中，进一步培养学生的数形结合意识，发展形象思维；‎ ‎2、在解决实际问题过程中，进一步发展学生的分析问题、解决问题的能力和数学应用意识．‎ ‎3、在现实问题的解决中，使学生初步认识数学与人类生活的密切联系，从而培养学生学习数学的兴趣．‎ 重点 一次函数图象的应用 难点 从函数图象中正确读取信息 教学用具 课件 教学环节 说 明 二次备课 复习 新课导入 内容：一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.‎ ‎(1)农民自带的零钱是多少?‎ ‎(2)试求降价前 与 之间的关系 ‎(3)由表达式你能求出降价前每千克的土豆价格是多少?‎ ‎(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?‎ 5‎ 课 程 讲 授 内容1：例1‎ 小聪和小慧去某风景区游览，约好在“飞瀑”见面，上午7：00小聪乘电动汽车从“古刹”出发，沿景区公路去“飞瀑”，车速为 ，小慧也于上午7：00从“塔林”出发，骑电动自行车沿景区公路去“飞瀑”，车速为．‎ ‎（1）当小聪追上小慧时，他们是否已经过了“草甸”？‎ ‎（2）当小聪到达“飞瀑”时，小慧离“飞瀑”还有多少千米？‎ 分析： ‎ 当小聪追上小慧时，说明他们两个人的什么量是相同的？是否已经过了“草甸”该用什么量来表示？你会选择用哪种方式来解决？图象法？还是解析法？‎ 解：设经过t时，小聪与小慧离“古刹”的路程分别为、，‎ 由题意得：， 将这两个函数解析式画在同一个直角坐标系上，观察图象，得 ‎⑴两条直线 ，的交点坐标为（1，36）‎ 这说明当小聪追上小慧时，，即离“古刹”，已超过，也就是说，他们已经过了“草甸”‎ ‎⑵当小聪到达“飞瀑”时，即，此时 ．‎ ‎ 所以小慧离“飞瀑”还有45－42.5=2.5（km）‎ 思考：用解析法如何求得这两个问题的结果？小聪、小慧运行时间与路程之间的关系式分别是什么（小聪的解析式为 ，小慧的解析式为)？‎ 5‎ 活动目的：培养学生的识图能力和探究能力，调动学生学习的自主意识．通过问题串的精心设计，引导学生根据实际问题建立适当的函数模型，利用该函数图象的特征解决这个问题．在此过程中渗透数形结合的思想方法，发展学生的数学应用能力．‎ 说明：在这个环节的学习过程中，如果学生入手感到困难，可用以下问题串引导学生进行分析。⑴两个人是否同时起步？ ‎ ‎⑵在两个人到达之前所用时间是否相同？所行驶的路程是否相同？出发地点是否相同？两个人的速度各是多少？⑶这个问题中的两个变量是什么？它们之间是什么函数关系？⑷如果用表示路程，表示时间，那么他们的函数解析式是一样？他们各自的解析式分别是什么？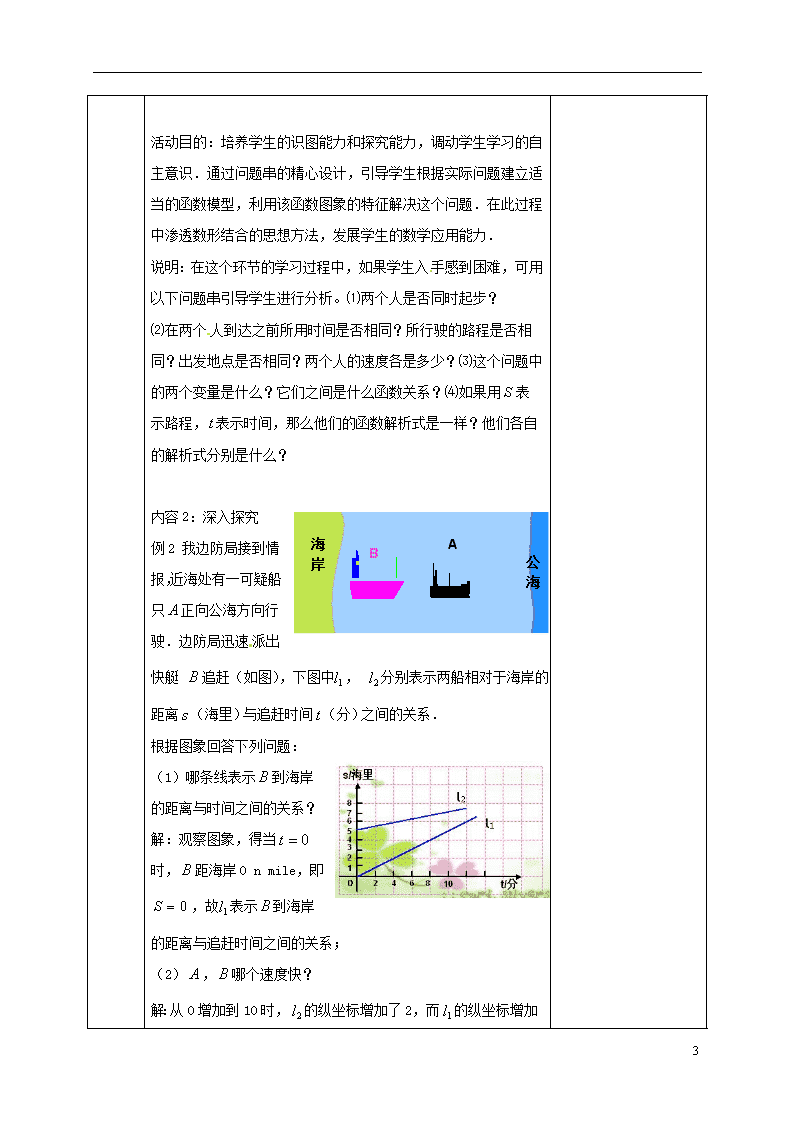‎ 内容2：海 岸 公 海 A B 深入探究 例2 我边防局接到情报，近海处有一可疑船只正向公海方向行驶．边防局迅速派出快艇 追赶（如图），下图中， 分别表示两船相对于海岸的距离（海里）与追赶时间（分）之间的关系．‎ 根据图象回答下列问题：‎ ‎（1）哪条线表示到海岸的距离与时间之间的关系？‎ 解：观察图象，得当时，距海岸0 n mile，即，故表示到海岸的距离与追赶时间之间的关系；‎ ‎（2），哪个速度快？‎ 解：从0增加到10时，的纵坐标增加了2，而 5‎ 的纵坐标增加了5，即10 min内，行驶了‎2海里，行驶了5 n mile，所以的速度快．‎ ‎（3）15 min内能否追上？‎ 解：可以看出，当时，上对应点在 上对应点的下方，‎ ‎（4）如果一直追下去，那么能否追上？‎ 解：如图 ，相交于点P．因此，如果一直追下去，那么一定能追上．‎ ‎（5）当逃到离海岸海里的公海时，将无法对其进行检查．照此速度，能否在逃到公海前将其拦截？‎ 解：从图中可以看出，与交点P的纵坐标小于，这说明在逃入公海前，我边防快艇能够追上．‎ 活动目的：培养学生良好的识图能力，进一步体会数与形的关系，建立良好的知识联系．‎ 说明：学生在教师的引导下，逐步形成了良好的识图能力．‎ 小结 本节课我们学 5‎ 习了一次函数图象的应用，在运用一次函数解决实际问题时，可以直接从函数图象上获取信息解决问题，当然也可以设法得出各自对应的函数关系式，然后借助关系式完全通过计算解决问题。通过列出关系式解决问题时，一般首先判断关系式的特征，如两个变量之间是不是一次函数关系？当确定是一次函数关系时，可求出函数解析式，并运用一次函数的图象和性质进一步求得我们所需要的结果．‎ 意图：引导学生自己小结运用一次函数解决实际问题的主要方法。‎ 说明：让学生畅所欲言，相互进行补充，尽量用自己的语言进行归纳总结。‎ 作业布置 板书设计 课后反思 5‎