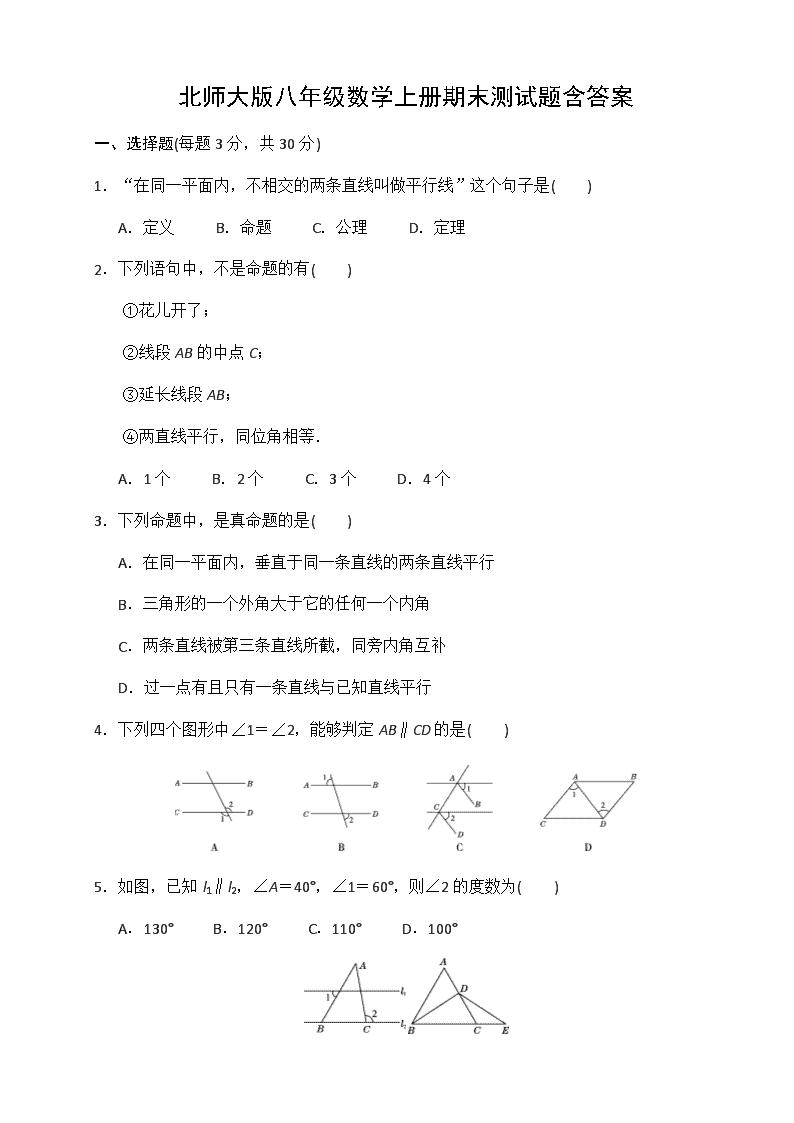北师大版八年级数学上册期末测试题含答案 8页

北师大版八年级数学上册期末测试题含答案 一、选择题(每题 3 分，共 30 分) 1．“在同一平面内，不相交的两条直线叫做平行线”这个句子是( ) A．定义 B．命题 C．公理 D．定理 2．下列语句中，不是．．命题的有( ) ①花儿开了； ②线段 AB 的中点 C； ③延长线段 AB； ④两直线平行，同位角相等． A．1 个 B．2 个 C．3 个 D．4 个 3．下列命题中，是真命题的是( ) A．在同一平面内，垂直于同一条直线的两条直线平行 B．三角形的一个外角大于它的任何一个内角 C．两条直线被第三条直线所截，同旁内角互补 D．过一点有且只有一条直线与已知直线平行 4．下列四个图形中∠1＝∠2，能够判定 AB∥CD 的是( ) 5．如图，已知 l1∥l2，∠A＝40°，∠1＝60°，则∠2 的度数为( ) A．130° B．120° C．110° D．100° (第 5 题) (第 6 题) 6．如图，已知在△ABC 中，点 D 在 AC 上，延长 BC 至 E，连接 DE，则下列结论不一定．．．成 立的是( ) A．∠DCE＞∠ADB B．∠ADB＞∠DBC C．∠ADB＞∠ACB D．∠ADB＞∠DEC 7．如图，∠AOB 的两边 OA，OB 均为平面反光镜，∠AOB＝40°，在射线 OB 上有一点 P， 从点 P 射出的一束光线经 OA 上的 Q 点反射后，反射光线 QR 恰好与 OB 平行，则∠QPB 的度数是( ) A．60° B．80° C．100° D．120° (第 7 题) 8．如图，在△ABC 中，D 是 AB 上一点，E 是 AC 上一点，BE，CD 相交于点 F，∠A＝70°， ∠ACD＝20°，∠ABE＝28°，则∠CFE 的度数是( ) A．62° B．68° C．78° D．90° (第 8 题) (第 9 题) (第 10 题) 9．如图，直线 l∥m，等边三角形 ABC 的顶点 B 在直线 m 上．若∠1＝20°，则∠2 的度数 为( ) A．60° B．45° C．40° D．30° 10．如图，∠ACD 是△ABC 的一个外角，CE 平分∠ACD，F 为 CA 延长线上的一点，FG∥CE， 且 FG 交 AB 于点 G.关于∠2＋∠3 与∠1 的大小关系，正确的是( ) A．∠2＋∠3＞∠1 B．∠2＋∠3＜∠1 C．∠2＋∠3＝∠1 D．无法判断 二、填空题(每题 3 分，共 30 分) 11．说明“互补的两个角，一定一个是锐角，一个是钝角”是假命题，可举出反例： ____________________________________________________. 12．将命题“平行于同一条直线的两条直线互相平行”改写成“如果……那么……”的形 式：_________________________________________． 13．如图，一把长方形直尺沿直线断开并错位，点 E，D，B，F 在同一条直线上，若∠ADE ＝126°，则∠DBC＝________. (第 13 题) (第 14 题) (第 15 题) (第 16 题) 14．如图，在△ABC 中，D 是 AB 延长线上一点．若∠A＝40°，∠CBD＝100°，则∠C＝________． 15．如图，把长方形 ABCD 沿 EF 对折后使两部分重合，若∠1＝50°，则∠AEF＝________. 16．将一副三角尺按如图所示放置，使点 A 在 DE 上，BC∥DE，则∠AFC＝________. 17．如图，直线 a∥b，直线 l 与 a 相交于点 P，与直线 b 相交于点 Q，PM⊥l 于点 P，若 ∠1＝50°，则∠2 的度数为________． (第 17 题) (第 18 题) (第 19 题) (第 20 题) 18．如图，∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝________． 19．如图，直线 l1∥l2，∠A＝125°，∠B＝85°，则∠1＋∠2＝________． 20．如图，AB＝BC＝CD＝DE＝EF＝FG，∠1＝130°，则∠A＝________． 三、解答题(21 题 8 分，26 题 12 分，其余每题 10 分，共 60 分) 21．已知命题：“如图，点 B，F，C，E 在同一条直线上，则 AB∥DE.”判断这个命题是真 命题还是假命题，如果是真命题，请给出证明；如果是假命题，在不添加其他辅助线 的情况下，请添加一个适当的条件使它成为真命题，并说明理由． (第 21 题) 22．如图，EF∥BC，AC 平分∠BAF，∠B＝80°，求∠C 的度数． (第 22 题) 23．如图，已知∠1＋∠2＝180°，∠DEF＝∠A，∠BED＝60°，求∠ACB 的度数． (第 23 题) 24．如图，在△ABC 中，D 是 BC 上一点，AD＝BD，∠C＝∠ADC，∠BAC＝57°，求∠DAC 的度数． (第 24 题) 25．如图，已知点 E 在 BD 上，AE⊥CE 且 EC 平分∠DEF. (1)求证：EA 平分∠BEF； (2)若∠1＝∠A，∠4＝∠C，求证：AB∥CD. (第 25 题) 26．如图，在△ABC 中，∠B＜∠ACB，AD 平分∠BAC，P 为线段 AD 上的一个动点，PE⊥AD， 且 PE 交直线 BC 于点 E. (1)若∠B＝35°，∠ACB＝85°，求∠E 的度数； (2)当 P 点在线段 AD 上运动时，求证：∠E＝1 2(∠ACB－∠B)． (第 26 题) 答案 一、1.A 2.C 3.A 4.B 5.D 6.A 7．B 8.A 9.C 10.C 二、11.两个角的度数都为 90° 12．如果两条直线都与同一条直线平行，那么这两条直线互相平行 13．54° 14.60° 15.115° 16.75° 17．40° 18.360° 19.30° 20．10° 解析：设∠A＝x.∵AB＝BC＝CD＝DE＝EF＝FG，∴根据等腰三角形的性质和三角 形外角的性质，得∠CDB＝∠CBD＝2x，∠DEC＝∠DCE＝3x，∠DFE＝∠EDF＝4x，∠FGE＝ ∠FEG＝5x，∴180°－5x＝130°，解得 x＝10°.∴∠A＝10°. 三、21.解：这个命题是假命题． 添加条件∠B＝∠E 使其成为真命题．理由：内错角相等，两直线平行．(添加条件不唯一) 22．解：∵EF∥BC， ∴∠BAF＝180°－∠B＝100°. ∵AC 平分∠BAF， ∴∠CAF＝1 2 ∠BAF＝50°. ∵EF∥BC， ∴∠C＝∠CAF＝50°. 23．解：∵∠1＋∠2＝180°， ∠1＋∠DFE＝180°， ∴∠2＝∠DFE. ∴AB∥EF. ∴∠BDE＝∠DEF. 又∵∠DEF＝∠A， ∴∠BDE＝∠A. ∴DE∥AC. ∴∠ACB＝∠DEB＝60°. 24．解：设∠DAC＝x，则∠BAD＝57°－x. ∵∠C＝∠ADC， ∴∠ADC＝1 2(180°－x)． 又∵AD＝BD， ∴∠B＝∠BAD＝57°－x. ∵∠ADC＝∠B＋∠BAD， ∴1 2(180°－x)＝2(57°－x)， 解得 x＝16°. 即∠DAC 的度数为 16°. 25．证明：(1)∵AE⊥CE， ∴∠AEC＝90°. ∴∠2＋∠3＝90°且∠1＋∠4＝90°. 又∵EC 平分∠DEF， ∴∠3＝∠4. ∴∠1＝∠2. ∴EA 平分∠BEF. (2)∵∠1＝∠A，∠4＝∠C， ∴∠1＋∠A＋∠4＋∠C＝2(∠1＋∠4)＝180°. ∴∠B＋∠D＝(180°－2∠1)＋(180°－2∠4)＝360°－2(∠1＋∠4)＝180°. ∴AB∥CD. 26．(1)解：∵∠B＝35°，∠ACB＝85°，∴∠BAC＝60°. ∵AD 平分∠BAC， ∴∠DAC＝∠BAD＝30°. ∴∠ADC＝65°. 又∵PE⊥AD， ∴∠DPE＝90°. ∴∠E＝25°. (2)证明：∵∠B＋∠BAC＋∠ACB＝180°， ∴∠BAC＝180°－(∠B＋∠ACB)． ∵AD 平分∠BAC， ∴∠BAD＝1 2 ∠BAC＝90°－1 2(∠B＋∠ACB)． ∴∠ADC＝∠B＋∠BAD＝90°－1 2(∠ACB－∠B)． ∵PE⊥AD， ∴∠DPE＝90°. ∴∠ADC＋∠E＝90°. ∴∠E＝90°－∠ADC. ∴∠E＝1 2(∠ACB－∠B)．