2020春八年级数学下册第18章函数及其图象18-3一次函数3一次函数的性质习题课件华东师大版 30页

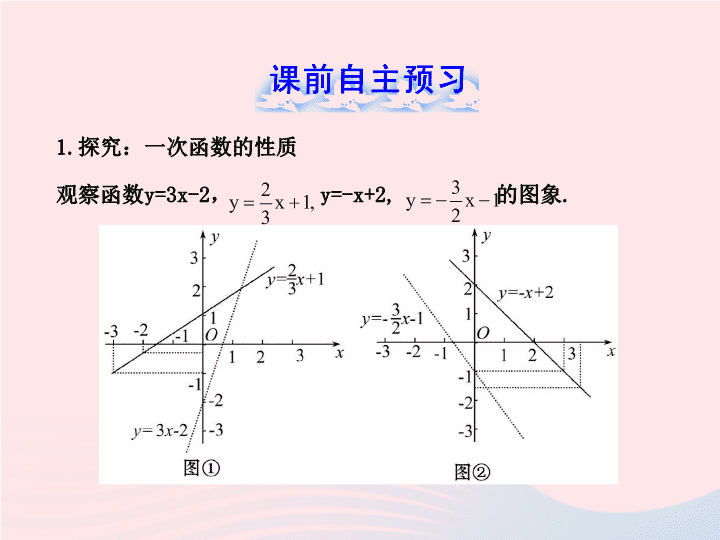
3.一次函数的性质 1.探究：一次函数的性质 观察函数y=3x-2， y=-x+2, 的图象. 如图①所示,在函数的图象中,我们看到:当一个点在直线上从左 向右移动(自变量x从小到大)时,它的位置也在逐步从___到___变 化(函数y的值也从___变到___)——图象自左向右是_____的,函数 值y随自变量x的增大而_____. 在图②中我们看到:当一个点在直线上从左向右移动(自变量x从 小到大)时,它的位置在逐步从___到___变化(函数y的值从___变到 ___)——图象自左向右是_____的,函数值y随自变量x的增大而___ ___. 低 高 小 大 上升 增大 高 低 大 小 下降 减 小 【归纳】一次函数y=kx+b(k≠0)的性质 (1)当k＞0时，y随x的增大而_____，这时函数图象从左到右_____. (2)当k＜0时，y随x的增大而_____，这时函数图象从左到右_____. 【点拨】一次函数y=kx+b中，b确定图象与y轴的交点，k确定图 象由左到右上升还是下降，|k|越大，上升或下降的速度越快. 增大 上升 减小 下降 2.结合图象理解一次函数y=kx+b(k,b为常数,k≠0)的性质 一、二、三 一、三、四 一、二、四 二、三、四 增大 增大 减小 减小 【预习思考】 1.函数y=-5x+3的图象经过哪几个象限？ 提示：y=-5x+3的图象过一、二、四象限. 2.如果一次函数y=kx-3的图象经过一、三、四象限，那么k的取 值是多少？ 提示：k＞0. 一次函数的性质 【例1】已知一次函数y=(5m-3)x+(2-n),其图象为直线， (1)当m，n取何值时,y随x的增大而减小； (2)当m，n取何值时,直线与y轴的交点在x轴的上方； (3)当m，n取何值时,直线y=(5m-3)x+(2-n)与直线y=3x平行. 【解题探究】 (1)①直线y=kx+b(k≠0),当k＜0时, y随x的增大而减小,与b的 取值无关； ②根据(1)①的探究,∵y随x的增大而减小,∴5m-3＜0,解得 即 n取任意数时,y随x的增大而减小. (2)①直线y=kx+b(k≠0)与y轴交点为(0,b),当b＞0时,直线与y 轴的交点在y轴的正半轴上,即交点在x轴的上方； ②根据(2)①的探究和一次函数的概念,可得 解得n<2 且 即当 时,直线与y轴的交点在x轴的上方； (3)①直线y1=k1x+b1与直线y2=k2x+b2(k1≠0,k2≠0),当 时,y1与y2平行； ②根据(3)①的探究,∵直线y=(5m-3)x+(2-n)与直线y=3x平行, 解得 即当 时,直线 y=(5m-3)x+(2-n)与直线y=3x平行. 【互动探究】两条直线y1=k1x+b1和y2=k2x+b2(k1·k2≠0)平行的 条件是k1=k2吗？ 提示：不是.两直线平行的条件除k1=k2外，还需b1≠b2，否则两 直线可能重合. 【规律总结】 一次函数性质“口诀” 一次函数是直线,经过(0,b)， k正左低右边高,越走越高像爬山； k负左高右边低,越来越低很明显； 直线位置k，b定,增减性质k来管. 【跟踪训练】 1.(2012·泉州中考)若y=kx-4的函数值y随x的增大而增大，则k 的值可能是下列的( ) (A)-4 (B) (C)0 (D)3 【解析】选D.由一次函数的性质可知，当k＞0时，函数值y随x 的增大而增大，只有选项D中的数大于0，故选D. 2.(2012·上海中考)已知正比例函数y=kx(k≠0)，点(2,-3)在 函数上，则y随x的增大而__________(“增大”或“减小”). 【解析】把点(2,-3)代入函数解析式得 所以y随x的 增大而减小. 答案：减小 3.已知一次函数y=(a-1)x+b的图象 如图所示,那么a的取值范围是__________. 【解析】由图象可以看出:函数图象自左 向右越来越高,呈上升趋势,即y随x的增大 而增大,∴a-1＞0,∴a＞1. 答案：a＞1 一次函数性质的应用 【例2】(8分)直线l:y=(m-3)x-(2-n)(m,n为常数)的图象如图所 示,化简:|m-n|-|n-2|-|m-1|. 【规范解答】 由函数图象得,y随x的增大而增大且与y轴 的交点在x轴下方, …………………………2分 解得m＞3且n＜2,………………………4分 ∴|m-n|-|n-2|-|m-1| =m-n-［-(n-2)］-(m-1)………………6分 =m-n+n-2-m+1…………………………7分 =-1.……………………………………8分 易错提醒:k，b的 条件同时考虑，不 可忽略任何一方. 【互动探究】 一次函数y=-2x+5当-1≤x≤3时，y的取值范围是什么？ 提示：-1≤y≤7.对于函数y=-2x+5，k=-2<0,故当x=-1时，y最 大为7；当x=3时，y最小为-1. 【规律总结】 一次函数性质应用的“四”种形态 (1)直线型图象:自变量取值范围是全体实数； (2)射线型图象:自变量取值的非负性(或受实际背景的限制)； (3)线段型图象:自变量取值的非负性(或受实际背景的限制)； (4)折线型图象:自变量取值的非负性(或受实际背景的限制). 【跟踪训练】 4.点P1(x1,y1),P2(x2,y2)是一次函数y=-4x+3图象上的两个点,且 x10,k<0.5；②2k+1=0且1-2k≠0,k= -0.5；③1-2k>0且2k+1≥0,-0.5≤k<0.5. 1.(2012·益阳中考)在一个标准大气压下，能反映水在均匀加 热过程中，水的温度(T)随加热时间(t)变化的函数图象大致是 ( ) 【解析】选B.在一个标准大气压下，水在沸腾之前是一次函数， 当水温达到100℃以后，水温不再升高，选项B反映水的温度(T) 随加热时间(t)变化的规律. 2.正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函 数y=x+k的图象大致是( ) 【解析】选A.∵正比例函数y=kx(k≠0)的函数值y随x的增大而 增大,∴k＞0,∴一次函数y=x+k的图象经过一、二、三象限. 3.在一次函数y=2x+3中,y随x的增大而__________(填“增大” 或“减小”),当0≤x≤5时,y的最小值为___________. 【解析】∵一次函数y=2x+3中,k=2＞0,∴y随x的增大而增大, ∴当x最小时y最小，故当0≤x≤5时,y的最小值为3. 答案：增大 3 4.(2011·广安中考)写出一个具体的y随x的增大而减小的一次 函数关系式__________. 【解析】∵一次函数y=kx+b的增减性与k的符号有关,而与b的符 号无关.当k＞0时,y随x的增大而增大；当k＜0时,y随x的增大而 减小.∴所写的一次函数y=kx+b只需满足k＜0即可.答案不唯一, 如:y＝-x+1. 答案：y＝-x+1(答案不唯一) 5.已知一次函数y=(3a-2)x+(1-b),求字母a,b的取值范围,使得: (1)y随x的增大而增大； (2)函数图象与y轴的交点在x轴的下方； (3)函数的图象过第一、二、四象限. 【解析】(1)由一次函数y=kx+b(k≠0)的性质可知: 当k＞0时,函数值y随x的增大而增大,即3a-2＞0,解得 且 b取任何实数. ∴当 且b取任何实数,y随x的增大而增大； (2)函数图象与y轴的交点为(0,1-b),∵交点在x轴的下方, 解得 且b＞1. ∴当 且b＞1时,函数图象与y轴的交点在x轴的下方； (3)函数图象过第一、二、四象限,则必须满足 解得 ∴当 时,函数的图象过第一、二、四象限.