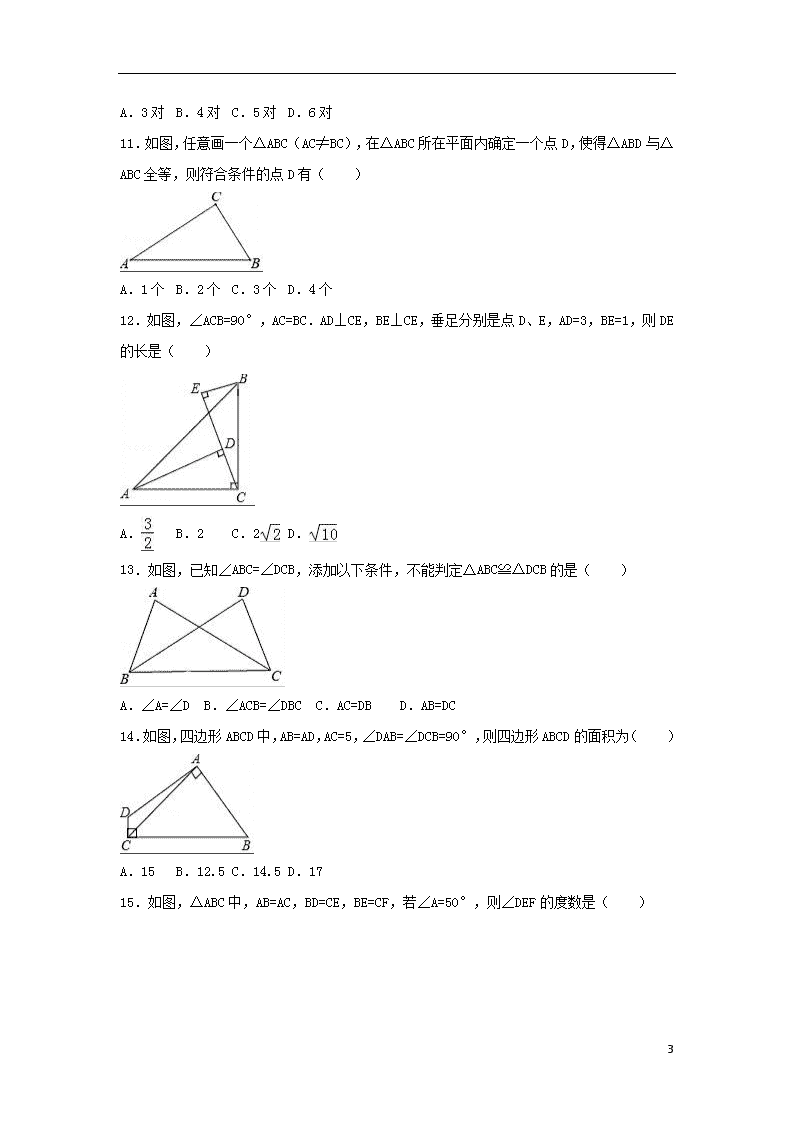2020八年级数学上册第12章全等三角形12 25页

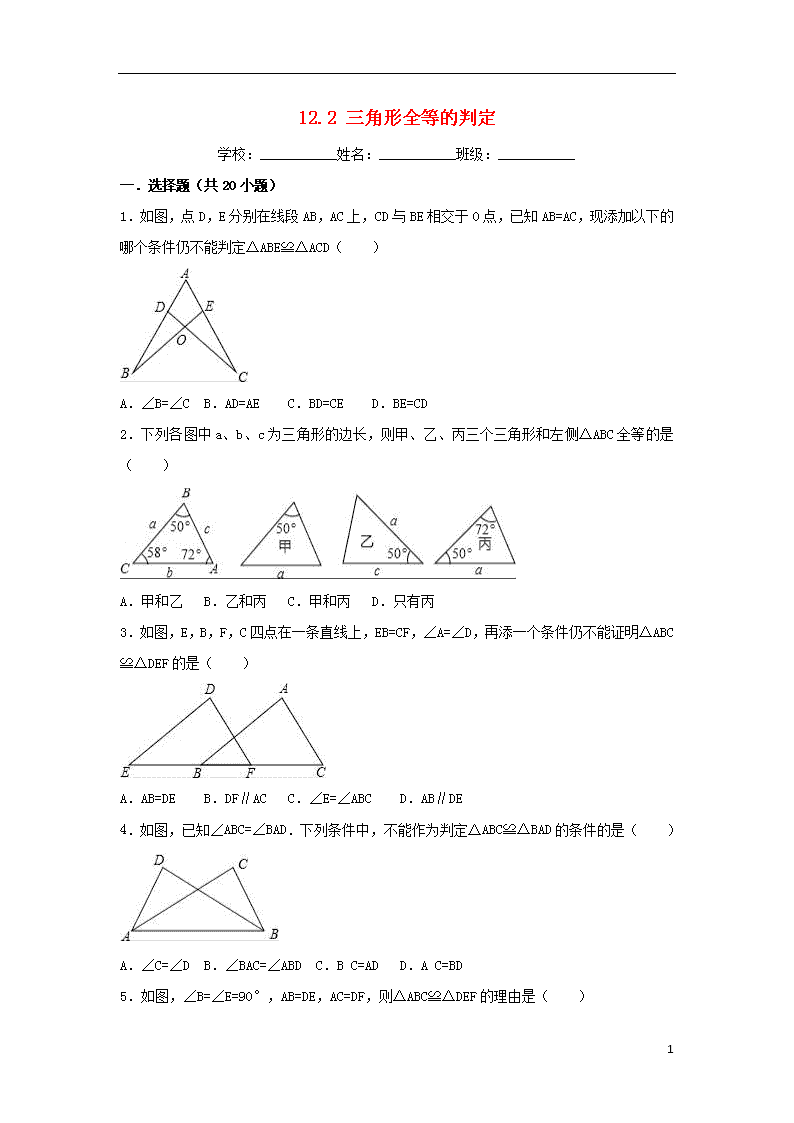
‎12.2 三角形全等的判定 学校：___________姓名：___________班级：___________‎ 一．选择题（共20小题）‎ ‎1．如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（　　）‎ A．∠B=∠C B．AD=AE C．BD=CE D．BE=CD ‎2．下列各图中a、b、c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是（　　）‎ A．甲和乙 B．乙和丙 C．甲和丙 D．只有丙 ‎3．如图，E，B，F，C四点在一条直线上，EB=CF，∠A=∠D，再添一个条件仍不能证明△ABC≌△DEF的是（　　）‎ A．AB=DE B．DF∥AC C．∠E=∠ABC D．AB∥DE ‎4．如图，已知∠ABC=∠BAD．下列条件中，不能作为判定△ABC≌△BAD的条件的是（　　）‎ A．∠C=∠D B．∠BAC=∠ABD C．B C=AD D．A C=BD ‎5．如图，∠B=∠E=90°，AB=DE，AC=DF，则△ABC≌△DEF的理由是（　　）‎ 25‎ A．SAS B．ASA C．AAS D．HL ‎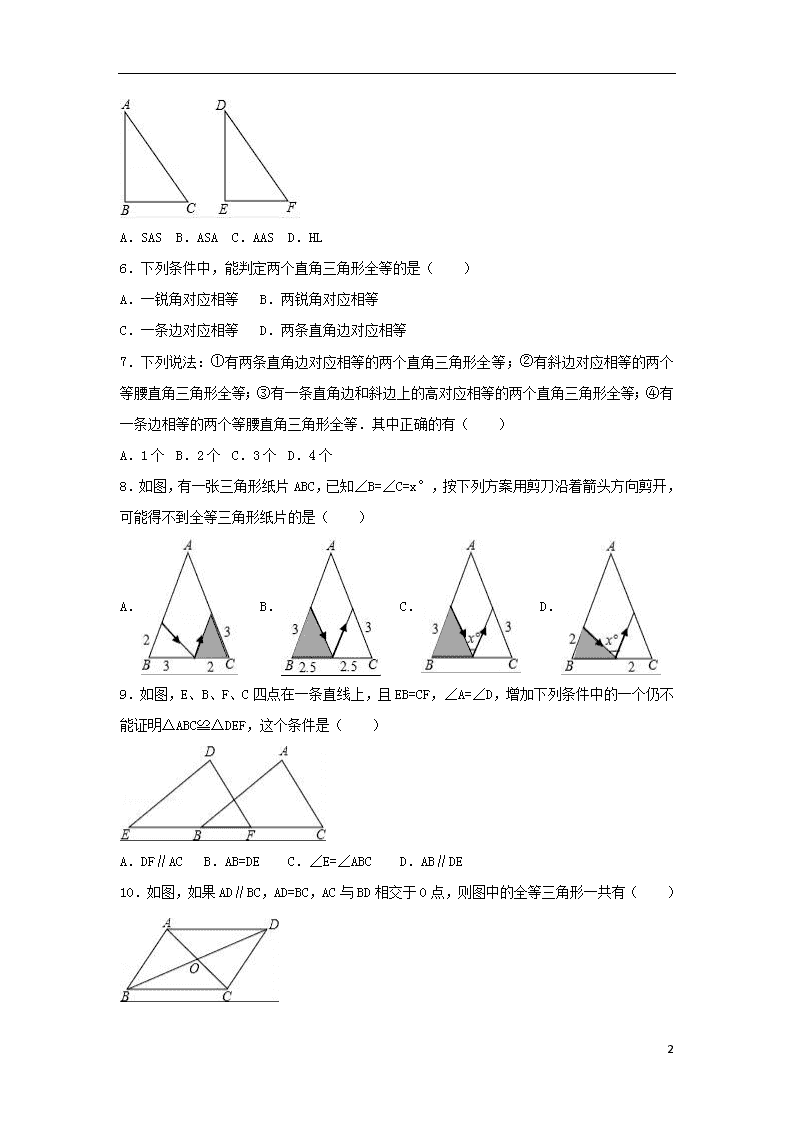6．下列条件中，能判定两个直角三角形全等的是（　　）‎ A．一锐角对应相等 B．两锐角对应相等 C．一条边对应相等 D．两条直角边对应相等 ‎7．下列说法：①有两条直角边对应相等的两个直角三角形全等；②有斜边对应相等的两个等腰直角三角形全等；③有一条直角边和斜边上的高对应相等的两个直角三角形全等；④有一条边相等的两个等腰直角三角形全等．其中正确的有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎8．如图，有一张三角形纸片ABC，已知∠B=∠C=x°，按下列方案用剪刀沿着箭头方向剪开，可能得不到全等三角形纸片的是（　　）‎ A． B． C． D．‎ ‎9．如图，E、B、F、C四点在一条直线上，且EB=CF，∠A=∠D，增加下列条件中的一个仍不能证明△ABC≌△DEF，这个条件是（　　）‎ A．DF∥AC B．AB=DE C．∠E=∠ABC D．AB∥DE ‎10．如图，如果AD∥BC，AD=BC，AC与BD相交于O点，则图中的全等三角形一共有（　　）‎ 25‎ A．3对 B．4对 C．5对 D．6对 ‎11．如图，任意画一个△ABC（AC≠BC），在△ABC所在平面内确定一个点D，使得△ABD与△ABC全等，则符合条件的点D有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎12．如图，∠ACB=90°，AC=BC．AD⊥CE，BE⊥CE，垂足分别是点D、E，AD=3，BE=1，则DE的长是（　　）‎ A． B．‎2 ‎C．2 D．‎ ‎13．如图，已知∠ABC=∠DCB，添加以下条件，不能判定△ABC≌△DCB的是（　　）‎ A．∠A=∠D B．∠ACB=∠DBC C．AC=DB D．AB=DC ‎14．如图，四边形ABCD中，AB=AD，AC=5，∠DAB=∠DCB=90°，则四边形ABCD的面积为（　　）‎ A．15 B．‎12.5 ‎C．14.5 D．17‎ ‎15．如图，△ABC中，AB=AC，BD=CE，BE=CF，若∠A=50°，则∠DEF的度数是（　　）‎ 25‎ A．75° B．70° C．65° D．60°‎ ‎16．如图，OA=OB，∠A=∠B，有下列3个结论：①△AOD≌△BOC，②△ACE≌△BDE，③点E在∠O的平分线上，其中正确的结论个数是（　　）‎ A．0 B．‎1 ‎C．2 D．3‎ ‎17．如图，将两根钢条AA′、BB′的中点 O连在一起，使AA′、BB′能绕着点O自由转动，就做成了一个测量工具，由三角形全等可知A′B′的长等于内槽宽AB，那么判定△OAB≌△OA′B′的理由是（　　）‎ A．SAS B．ASA C．SSS D．AAS ‎18．如图，一块三角形玻璃碎成了4块，现在要到玻璃店去配一块与原来的三角形玻璃完全一样的玻璃，那么最省事的办法是带（　　）去．‎ A．① B．② C．③ D．④‎ ‎19．如图所示，为了测量出A，B两点之间的距离，在地面上找到一点C，连接BC，AC，使∠ACB=90°，然后在BC的延长线上确定D，使CD=BC，那么只要测量出AD的长度也就得到了A，B两点之间的距离，这样测量的依据是（　　）‎ 25‎ A．AAS B．SAS C．ASA D．SSS ‎20．如图所示，小明书上的三角形被墨水污染了，他根据所学知识画出了完全一样的一个三角形，他根据的定理是（　　）‎ A．SSS B．SAS C．AAS D．ASA ‎　‎ 二．填空题（共8小题）‎ ‎21．如图，在△ABC和△DEF中，点B，F，C，E在同一直线上，BF=CE，AB∥DE，请添加一个条件，使△ABC≌△DEF，这个添加的条件可以是　 　（只需写一个，不添加辅助线）．‎ ‎22．如图，△ABC的两条高AD，BE相交于点F，请添加一个条件，使得△ADC≌△BEC（不添加其他字母及辅助线），你添加的条件是　 　．‎ ‎23．如图，AB=12，CA⊥AB于A，DB⊥AB于B，且AC=‎4m，P点从B向A运动，每分钟走‎1m 25‎ ‎，Q点从B向D运动，每分钟走‎2m，P、Q两点同时出发，运动　 　分钟后△CAP与△PQB全等．‎ ‎24．如图，AC⊥BC，AD⊥BD，垂足分别是C、D，若要用“HL”得到Rt△ABC≌Rt△BAD，则你添加的条件是　 　．（写一种即可）‎ ‎25．如图，Rt△ABC中，∠BAC=90°，AB=AC，分别过点B、C作过点A的直线的垂线BD、CE，垂足分别为D、E，若BD=3，CE=2，则DE=　 　．‎ ‎26．如图，AB与CD相交于E，AE=EB，CE=ED，D为线段FB的中点，CF与AB交于点G，若AB=18，则GE之长为　 　．‎ ‎27．现有A、B两个大型储油罐，它们相距‎2km，计划修建一条笔直的输油管道，使得A、B两个储油罐到输油管道所在直线的距离都为‎0.5km，输油管道所在直线符合上述要求的设计方案有　 　种．‎ ‎28．如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△‎ 25‎ ADC，这样就有∠QAE=∠PAE．则说明这两个三角形全等的依据是　 　．‎ ‎　‎ 三．解答题（共8小题）‎ ‎29．如图，∠A=∠B，AE=BE，点D在AC边上，∠1=∠2，AE和BD相交于点O． 求证：△AEC≌△BED；‎ ‎30．如图，点E，H，G，N在一条直线上，∠F=∠M，EH=GN，MH∥FG．求证：△EFG≌△NMH．‎ 25‎ ‎31．如图，已知Rt△ABC中，∠ACB=90°，CA=CB，D是AC上一点，E在BC的延长线上，且AE=BD，BD的延长线与AE交于点F．试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系，并说明你猜想的正确性．‎ ‎32．如图，在△ABC中，AB=AC，DE是过点A的直线，BD⊥DE于D，CE⊥DE于点E；‎ ‎（1）若B、C在DE的同侧（如图所示）且AD=CE．求证：AB⊥AC；‎ ‎（2）若B、C在DE的两侧（如图所示），其他条件不变，AB与AC仍垂直吗？若是请给出证明；若不是，请说明理由．‎ 25‎ ‎33．如图，△ABC中，D是BC边上一点，E是AD的中点，过点A作BC的平行线交BE的延长线于F，且AF=CD，连接CF．‎ ‎（1）求证：△AEF≌△DEB；‎ ‎（2）若AB=AC，试判断四边形ADCF的形状，并证明你的结论．‎ ‎34．如图，∠A=∠D=90°，AC=DB，AC、DB相交于点O．求证：OB=OC．‎ 25‎ ‎35．如图，有一个池塘，要到池塘两侧AB的距离，可先在平地上取一个点C，从C不经过池塘可以到达点A和B，连接AC并延长到点D，使CD=CA，连接BC并延长到点E，使CE=CB，连接DE，那么量出DE的长就是A，B的距离，为什么？‎ ‎36．小强为了测量一幢高楼高AB，在旗杆CD与楼之间选定一点P．测得旗杆顶C视线PC与地面夹角∠DPC=36°，测楼顶A视线PA与地面夹角∠APB=54°，量得P到楼底距离PB与旗杆高度相等，等于‎10米，量得旗杆与楼之间距离为DB=‎36米，小强计算出了楼高，楼高AB是多少米？‎ ‎　‎ 参考答案与试题解析 ‎　‎ 一．选择题（共20小题）‎ ‎1．‎ 解：∵AB=AC，∠A为公共角，‎ A、如添加∠B=∠C，利用ASA即可证明△ABE≌△ACD；‎ B、如添AD=AE，利用SAS即可证明△ABE≌△ACD；‎ C、如添BD=CE，等量关系可得AD=AE，利用SAS即可证明△ABE≌△ACD；‎ D、如添BE=CD，因为SSA，不能证明△ABE≌△ACD，所以此选项不能作为添加的条件．‎ 25‎ 故选：D．‎ ‎　‎ ‎2．‎ 解：乙和△ABC全等；理由如下：‎ 在△ABC和图乙的三角形中，满足三角形全等的判定方法：SAS，‎ 所以乙和△ABC全等；‎ 在△ABC和图丙的三角形中，满足三角形全等的判定方法：AAS，‎ 所以丙和△ABC全等；‎ 不能判定甲与△ABC全等；‎ 故选：B．‎ ‎　‎ ‎3．‎ 解：A、添加DE=AB与原条件满足SSA，不能证明△ABC≌△DEF，故A选项正确．‎ B、添加DF∥AC，可得∠DFE=∠ACB，根据AAS能证明△ABC≌△DEF，故B选项错误．‎ C、添加∠E=∠ABC，根据AAS能证明△ABC≌△DEF，故C选项错误．‎ D、添加AB∥DE，可得∠E=∠ABC，根据AAS能证明△ABC≌△DEF，故D选项错误．‎ 故选：A．‎ ‎　‎ ‎4．‎ 解：A、添加∠C=∠D时，可利用AAS判定△ABC≌△BAD，故此选项不符合题意；‎ B、添加∠BAC=∠ABD，根据ASA判定△ABC≌△BAD，故此选项不符合题意；‎ C、添加AB=DC，根据SAS能判定△ABC≌△BAD，故此选项不符合题意；‎ D、添加AC=DB，不能判定△ABC≌△BAD，故此选项符合题意；‎ 故选：D．‎ ‎　‎ ‎5．‎ 解：∵在Rt△ABC与Rt△DEF中，‎ ‎，‎ ‎∴Rt△ABC≌Rt△DEF（HL）．‎ 25‎ 故选：D．‎ ‎　‎ ‎6．‎ 解：两直角三角形隐含一个条件是两直角相等，要判定两直角三角形全等，起码还要两个条件，故可排除A、C；‎ 而B构成了AAA，不能判定全等；‎ D构成了SAS，可以判定两个直角三角形全等．‎ 故选：D．‎ ‎　‎ ‎7．‎ 解：①有两条直角边对应相等的两个直角三角形全等，可利用SAS判定两直角三角形全等；‎ ‎②有斜边对应相等的两个等腰直角三角形全等，可利用ASA判定两直角三角形全等；‎ ‎③有一条直角边和斜边上的高对应相等的两个直角三角形全等，能判定两直角三角形全等；‎ ‎④有一条边相等的两个等腰直角三角形全等，不能判定两直角三角形全等．‎ 故选：C．‎ ‎　‎ ‎8．‎ 解：A、由全等三角形的判定定理SAS证得图中两个小三角形全等，‎ 故本选项不符合题意；‎ B、由全等三角形的判定定理SAS证得图中两个小三角形全等，‎ 故本选项不符合题意；‎ C、如图1，∵∠DEC=∠B+∠BDE，‎ ‎∴x°+∠FEC=x°+∠BDE，‎ ‎∴∠FEC=∠BDE，‎ 所以其对应边应该是BE和CF，而已知给的是BD=FC=3，‎ 所以不能判定两个小三角形全等，故本选项符合题意；‎ D、如图2，∵∠DEC=∠B+∠BDE，‎ ‎∴x°+∠FEC=x°+∠BDE，‎ ‎∴∠FEC=∠BDE，‎ ‎∵BD=FC=2，∠B=∠C，‎ 25‎ ‎∴△BDE≌△CEF，‎ 所以能判定两个小三角形全等，故本选项不符合题意；‎ 由于本题选择可能得不到全等三角形纸片的图形，‎ 故选：C．‎ ‎　‎ ‎9．‎ 解：‎ ‎∵EB=CF，‎ ‎∴EB+BF=BF+CF，即EF=BC，且∠A=∠D，‎ ‎∴当DF∥AC时，可得∠DFE=∠C，满足AAS，可证明全等；‎ 当AB=DE时，满足ASS，不能证明全等；‎ 当∠E=∠ABC时，满足ASA，可证明全等；‎ 当AB∥DE时，可得∠E=∠ABC，满足ASA，可证明全等；‎ 故选：B．‎ ‎　‎ ‎10．‎ 解：共4对，△ABD≌△CDB，△ACD≌△CAB，△AOD≌△COB，△AOB≌△COD，‎ 理由是：∵AD∥BC，AD=BC，‎ ‎∴四边形ABCD是平行四边形，‎ 25‎ ‎∴AB=CD．‎ 在△ABD和△CDB中，‎ ‎，‎ ‎∴△ABD≌△CDB（SSS），‎ 同理△ACD≌△CAB，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴OA=OC，OB=OD，‎ ‎∵∠AOB=∠COD，‎ ‎∴△AOB≌△COD，‎ 同理△AOD≌△COB，‎ 故选：B．‎ ‎　‎ ‎11．‎ 解：如图所示，∵AB为公共边，‎ ‎∴D点有4种可能的位置（含D与C重合），‎ 故选：D．‎ ‎　‎ ‎12．‎ 解：∵BE⊥CE，AD⊥CE，‎ ‎∴∠E=∠ADC=90°，‎ ‎∴∠EBC+∠BCE=90°．‎ ‎∵∠BCE+∠ACD=90°，‎ ‎∴∠EBC=∠DCA．‎ 25‎ 在△CEB和△ADC中，‎ ‎，‎ ‎∴△CEB≌△ADC（AAS），‎ ‎∴BE=DC=1，CE=AD=3．‎ ‎∴DE=EC﹣CD=3﹣1=2‎ 故选：B．‎ ‎　‎ ‎13．‎ 解：A、∠A=∠D，∠ABC=∠DCB，BC=BC，符合AAS，即能推出△ABC≌△DCB，故本选项错误；‎ B、∠ABC=∠DCB，BC=CB，∠ACB=∠DBC，符合ASA，即能推出△ABC≌△DCB，故本选项错误；‎ C、∠ABC=∠DCB，AC=BD，BC=BC，不符合全等三角形的判定定理，即不能推出△ABC≌△DCB，故本选项正确；‎ D、AB=DC，∠ABC=∠DCB，BC=BC，符合SAS，即能推出△ABC≌△DCB，故本选项错误；‎ 故选：C．‎ ‎　‎ ‎14．‎ 解：如图，过A作AE⊥AC，交CB的延长线于E，‎ ‎∵∠DAB=∠DCB=90°，‎ ‎∴∠D+∠ABC=180°=∠ABE+∠ABC，‎ ‎∴∠D=∠ABE，‎ 又∵∠DAB=∠CAE=90°，‎ ‎∴∠CAD=∠EAB，‎ 又∵AD=AB，‎ ‎∴△ACD≌△AEB，‎ 25‎ ‎∴AC=AE，即△ACE是等腰直角三角形，‎ ‎∴四边形ABCD的面积与△ACE的面积相等，‎ ‎∵S△ACE=×5×5=12.5，‎ ‎∴四边形ABCD的面积为12.5，‎ 故选：B．‎ ‎　‎ ‎15．‎ 解：∵AB=AC，‎ ‎∴∠B=∠C，‎ 在△DBE和△ECF中，‎ ‎，‎ ‎∴△DBE≌△ECF（SAS），‎ ‎∴∠EFC=∠DEB，‎ ‎∵∠A=50°，‎ ‎∴∠C=（180°﹣50°）÷2=65°，‎ ‎∴∠CFE+∠FEC=180°﹣65°=115°，‎ ‎∴∠DEB+∠FEC=115°，‎ ‎∴∠DEF=180°﹣115°=65°，‎ 故选：C．‎ ‎　‎ ‎16．‎ 解：∵OA=OB，∠A=∠B，∠O=∠O，‎ ‎∴△AOD≌△BOC（ASA），故①正确；‎ ‎∴OD=CO，‎ ‎∴BD=AC，‎ 25‎ ‎∴△ACE≌△BDE（AAS），故②正确；‎ ‎∴AE=BE，‎ 连接OE，∴△AOE≌△BOE（SSS），‎ ‎∴∠AOE=∠BOE，‎ ‎∴点E在∠O的平分线上，故③正确，‎ 故选：D．‎ ‎　‎ ‎17．‎ 解：∵O是AA′、BB′的中点，‎ ‎∴AO=A′O，BO=B′O，‎ 在△OAB和△OA′B′中，‎ ‎∴△OAB≌△OA′B′（SAS），‎ 故选：A．‎ ‎　‎ ‎18．‎ 解：第①块只保留了原三角形的一个角和部分边，根据这块不能配一块与原来完全一样的；‎ 第②、③只保留了原三角形的部分边，根据这两块中的任一块均不能配一块与原来完全一样的；‎ 第④块不仅保留了原来三角形的两个角还保留了一边，则可以根据ASA来配一块一样的玻璃．‎ 最省事的方法是应带④去，‎ 故选：D．‎ ‎　‎ ‎19．‎ 解：∵AC⊥BD，‎ ‎∴∠ACB=∠ACD=90°，‎ 在△ACB和△ACD中，‎ ‎，‎ ‎∴△ACB≌△ACD（SAS），‎ 25‎ ‎∴AB=AD（全等三角形的对应边相等）．‎ 故选：B．‎ ‎　‎ ‎20．‎ 解：小明书上的三角形被墨水污染了，他根据所学知识画出了完全一样的一个三角形，‎ 他根据的定理是：两角及其夹边分别相等的两个三角形全等（ASA）．‎ 故选：D．‎ ‎　‎ 二．填空题（共8小题）‎ ‎21．‎ 解：添加AB=ED，‎ ‎∵BF=CE，‎ ‎∴BF+FC=CE+FC，‎ 即BC=EF，‎ ‎∵AB∥DE，‎ ‎∴∠B=∠E，‎ 在△ABC和△DEF中，‎ ‎∴△ABC≌△DEF（SAS），‎ 故答案为：AB=ED．‎ ‎　‎ ‎22．‎ 解：添加AC=BC，‎ ‎∵△ABC的两条高AD，BE，‎ ‎∴∠ADC=∠BEC=90°，‎ ‎∴∠DAC+∠C=90°，∠EBC+∠C=90°，‎ 25‎ ‎∴∠EBC=∠DAC，‎ 在△ADC和△BEC中，‎ ‎∴△ADC≌△BEC（AAS），‎ 故答案为：AC=BC．‎ ‎　‎ ‎23．‎ 解：∵CA⊥AB于A，DB⊥AB于B，‎ ‎∴∠A=∠B=90°，‎ 设运动x分钟后△CAP与△PQB全等；‎ 则BP=xm，BQ=2xm，则AP=（12﹣x）m，‎ 分两种情况：‎ ‎①若BP=AC，则x=4，‎ AP=12﹣4=8，BQ=8，AP=BQ，‎ ‎∴△CAP≌△PBQ；‎ ‎②若BP=AP，则12﹣x=x，‎ 解得：x=6，BQ=12≠AC，‎ 此时△CAP与△PQB不全等；‎ 综上所述：运动4分钟后△CAP与△PQB全等；‎ 故答案为：4．‎ ‎　‎ ‎24．‎ 解：可添加AC=BD，‎ ‎∵AC⊥BC，AD⊥BD，‎ ‎∴∠C=∠D=90°，‎ 在Rt△ABC和Rt△BAD中，‎ ‎∵，‎ ‎∴Rt△ABC≌Rt△BAD（HL），‎ 故答案为：AC=BD．‎ 25‎ ‎　‎ ‎25．‎ 解：∵∠BAC=90°，‎ ‎∴∠BAD+∠CAE=90°，‎ ‎∵BD⊥DE，‎ ‎∴∠BDA=90°，‎ ‎∴∠BAD+∠DBA=90°，‎ ‎∴∠DBA=∠CAE，‎ ‎∵CE⊥DE，‎ ‎∴∠E=90°，‎ 在△BDA和△AEC中，‎ ‎，‎ ‎∴△BDA≌△AEC（AAS），‎ ‎∴DA=CE=2，AE=DB=3，‎ ‎∴ED=5．‎ ‎　‎ ‎26．‎ 解：∵AE=EB，CE=ED，∠AEC=∠BED，‎ ‎∴△AEC≌△BED，‎ ‎∴∠ACE=∠EDB，∠EAC=∠EBD，AC=BD，‎ 又∵D为线段FB的中点，‎ ‎∴AC=FD，AC∥FD，‎ ‎∴四边形ACFD为平行四边形，‎ ‎∴△AGC∽△BGF，‎ 25‎ ‎∴，‎ ‎∵AB=18，‎ ‎∴AG=6，‎ ‎∵AE=EB=9，‎ ‎∴GE=AE﹣AG=9﹣6=3．‎ 故答案为：3‎ ‎　‎ ‎27．‎ 解：输油管道所在直线符合上述要求的设计方案有4种，如图所示；‎ 故答案为4．‎ ‎　‎ ‎28．‎ 解：在△ADC和△ABC中，‎ ‎，‎ ‎∴△ADC≌△ABC（SSS）．‎ ‎∴∠DAC=∠BAC，‎ 即∠QAE=∠PAE．‎ 故答案为：SSS．‎ ‎　‎ 三．解答题（共8小题）‎ ‎29．‎ 证明：∵AE和BD相交于点O，‎ ‎∴∠AOD=∠BOE．‎ 在△AOD和△BOE中，‎ 25‎ ‎∠A=∠B，∴∠BEO=∠2．‎ 又∵∠1=∠2，‎ ‎∴∠1=∠BEO，‎ ‎∴∠AEC=∠BED．‎ 在△AEC和△BED中，‎ ‎，‎ ‎∴△AEC≌△BED（ASA）．‎ ‎　‎ ‎30．‎ 证明：∵EH=GN，‎ ‎∴EG=NH，‎ ‎∵MH∥FG，‎ ‎∴∠EGF=∠NHM，‎ ‎∴在△EFG和△NMH中 ‎∴△EFG≌△NMH．‎ ‎　‎ ‎31．‎ 解：猜想：BF⊥AE．‎ 理由：∵∠ACB=90°，‎ ‎∴∠ACE=∠BCD=90°．‎ 又BC=AC，BD=AE，‎ ‎∴△BDC≌△AEC（HL）．‎ ‎∴∠CBD=∠CAE．‎ 又∴∠CAE+∠E=90°．‎ ‎∴∠EBF+∠E=90°．‎ ‎∴∠BFE=90°，即BF⊥AE．‎ ‎　‎ ‎32．‎ 25‎ ‎（1）证明：∵BD⊥DE，CE⊥DE，‎ ‎∴∠ADB=∠AEC=90°，‎ 在Rt△ABD和Rt△ACE中，‎ ‎∵，‎ ‎∴Rt△ABD≌Rt△CAE．‎ ‎∴∠DAB=∠ECA，∠DBA=∠ACE．‎ ‎∵∠DAB+∠DBA=90°，∠EAC+∠ACE=90°，‎ ‎∴∠BAD+∠CAE=90°．‎ ‎∠BAC=180°﹣（∠BAD+∠CAE）=90°．‎ ‎∴AB⊥AC．‎ ‎（2）AB⊥AC．理由如下：‎ 同（1）一样可证得Rt△ABD≌Rt△ACE．‎ ‎∴∠DAB=∠ECA，∠DBA=∠EAC，‎ ‎∵∠CAE+∠ECA=90°，‎ ‎∴∠CAE+∠BAD=90°，即∠BAC=90°，‎ ‎∴AB⊥AC．‎ ‎　‎ ‎33．‎ 证明：（1）∵E是AD的中点，‎ ‎∴AE=DE，‎ ‎∵AF∥BC，‎ ‎∴∠AFE=∠DBE，∠EAF=∠EDB，‎ 25‎ ‎∴△AEF≌△DEB（AAS）；‎ ‎（2）连接DF，‎ ‎∵AF∥CD，AF=CD，‎ ‎∴四边形ADCF是平行四边形，‎ ‎∵△AEF≌△DEB，‎ ‎∴BE=FE，‎ ‎∵AE=DE，‎ ‎∴四边形ABDF是平行四边形，‎ ‎∴DF=AB，‎ ‎∵AB=AC，‎ ‎∴DF=AC，‎ ‎∴四边形ADCF是矩形．‎ ‎　‎ ‎34．‎ 证明：在Rt△ABC和Rt△DCB中 ‎，‎ ‎∴Rt△ABC≌Rt△DCB（HL），‎ ‎∴∠OBC=∠OCB，‎ ‎∴BO=CO．‎ ‎　‎ ‎35．‎ 解：量出DE的长就等于AB的长，理由如下：‎ 在△ABC和△DEC中，，‎ ‎∴△ABC≌△DEC（SAS），‎ ‎∴AB=DE．‎ 25‎ ‎　‎ ‎36．‎ 解：∵∠CPD=36°，∠APB=54°，∠CDP=∠ABP=90°，‎ ‎∴∠DCP=∠APB=54°，‎ 在△CPD和△PAB中 ‎∵，‎ ‎∴△CPD≌△PAB（ASA），‎ ‎∴DP=AB，‎ ‎∵DB=36，PB=10，‎ ‎∴AB=36﹣10=26（m），‎ 答：楼高AB是26米．‎ ‎　‎ 25‎