2009中考数学分类汇编-阅读理解题 7页

阅读理解题分类汇编——广东中山 邓凯 一、选择题 ‎1.(2009年鄂州)为了求的值，可令S＝，则2S＝ ，因此2S-S＝，所以＝仿照以上推理计算出的值是（ ）‎ A. B. C. D.‎ 二、填空题 ‎2.（2009丽水市）用配方法解方程时，方程的两边同加上 ，使得方程左边配成一个完全平方式．‎ ‎【答案】填4.‎ ‎3.（2009绵阳市）将正整数依次按下表规律排成四列，则根据表中的排列规律，‎ 数2009应排的位置是第 行第 列．‎ 第1列 第2列 第3列 第4列 第1行 ‎1‎ ‎2‎ ‎3‎ 第2行 ‎6‎ ‎5‎ ‎4‎ 第3行 ‎7‎ ‎8‎ ‎9‎ 第4行 ‎12‎ ‎11‎ ‎10‎ ‎……‎ ‎4．（2009年中山）小明用下面的方法求出方程的解，请你仿照他的方法求出下面另外两个方程的解，并把你的解答过程填写在下面的表格中．‎ 方程 换元法得新方程 解新方程 检验 求原方程的解 令 则 所以 ‎5．（2009年漳州）阅读材料，解答问题．‎ 例 用图象法解一元二次不等式：．‎ 解：设，则是的二次函数．‎ 抛物线开口向上．‎ 又当时，，解得．‎ 由此得抛物线的大致图象如图所示．‎ 观察函数图象可知：当或时，．‎ 的解集是：或．‎ ‎（1）观察图象，直接写出一元二次不等式：的解集是____________；‎ ‎（2）仿照上例，用图象法解一元二次不等式：．（大致图象画在答题卡上）‎ ‎1‎ ‎2‎ ‎3‎ ‎1‎ ‎2‎ ‎3‎ x y ‎ ‎ ‎6．（2009年山西省）根据山西省统计信息网公布的数据，绘制了山西省2004~2008固定电话和移动电话年末用户条形统计图如下：‎ ‎0‎ ‎200‎ ‎400‎ ‎600‎ ‎800‎ ‎1000‎ ‎1200‎ ‎1400‎ ‎1600‎ ‎1800‎ 年份 万户 固定电话年末用户 移动电话年末用户 ‎2004‎ ‎2005‎ ‎2006‎ ‎2007‎ ‎2008‎ ‎721.3‎ ‎753.8‎ ‎897.8‎ ‎906.2‎ ‎885.4‎ ‎989.6‎ ‎859.0‎ ‎1420.4‎ ‎1689.5‎ ‎803.0‎ ‎（1）填空：2004~2008移动电话年末用户的极差是 万户，固定电话年末用户的中位数是 万户；‎ ‎（2）你还能从图中获取哪些信息？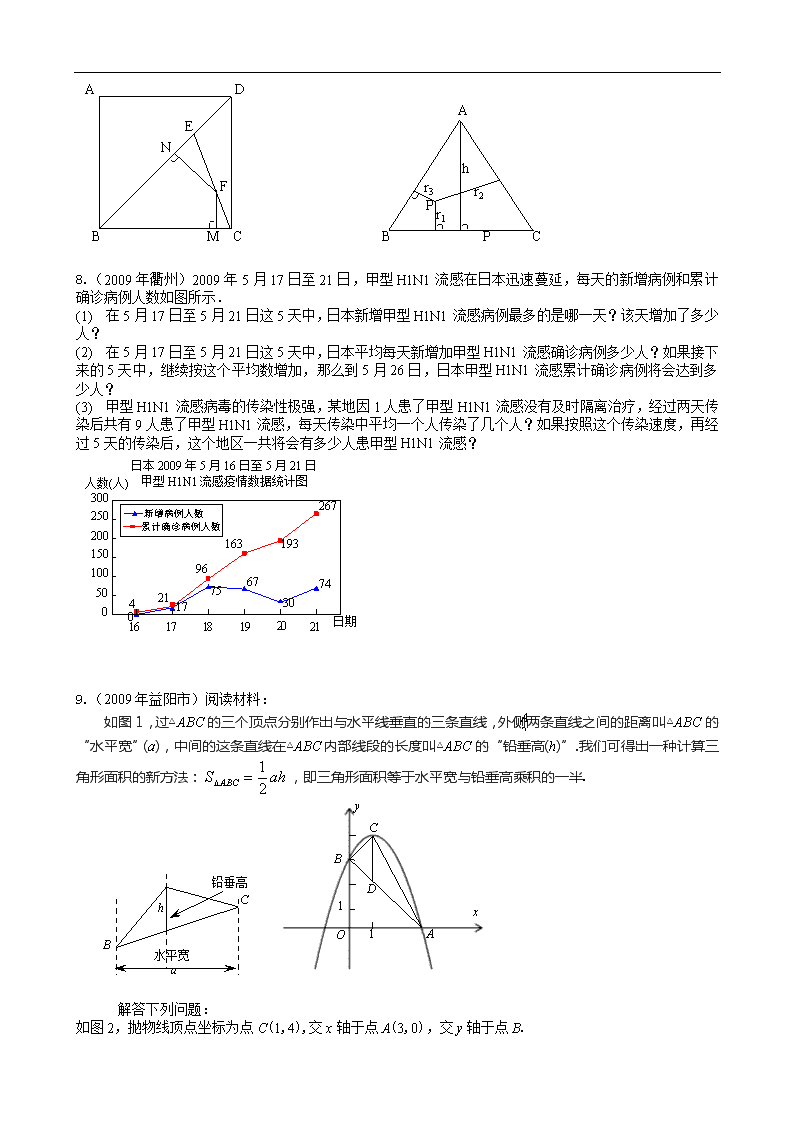请写出两条．‎ 三、解答题 ‎7.(2009年四川省内江市)阅读材料：如图，△ABC中，AB=AC，P为底边BC上任意一点，点P到两腰的距离分别为，腰上的高为h，连结AP，则 即：‎ ‎（定值）‎ ‎（1）理解与应用 如图，在边长为3的正方形ABC中，点E为对角线BD上的一点，‎ 且BE=BC，F为CE上一点，FM⊥BC于M，FN⊥BD于N，‎ 试利用上述结论求出FM+FN的长。‎ ‎（2）类比与推理 如果把“等腰三角形”改成“等到边三角形”，‎ 那么P的位置可以由“在底边上任一点”‎ 放宽为“在三角形内任一点”，即：‎ 已知等边△ABC内任意一点P到各边的距离分别为，‎ 等边△ABC的高为h，试证明：（定值）。‎ ‎（3）拓展与延伸 若正n边形A‎1A2…An内部任意一点P到各边的距离为 ‎，请问是否为定值，‎ 如果是，请合理猜测出这个定值。‎ A D B M C E N F ‎ ‎A B P C h r1‎ r2‎ r3‎ P ‎8.（2009年衢州）‎2009年5月17日至21日，甲型H1N1流感在日本迅速蔓延，每天的新增病例和累计确诊病例人数如图所示．‎ ‎(1)　在‎5月17日至‎5月21日这5天中，日本新增甲型H1N1流感病例最多的是哪一天？该天增加了多少人？‎ ‎(2)　在‎5月17日至‎5月21日这5天中，日本平均每天新增加甲型H1N1流感确诊病例多少人？如果接下来的5天中，继续按这个平均数增加，那么到‎5月26日，日本甲型H1N1流感累计确诊病例将会达到多少人？‎ ‎(3)　甲型H1N1流感病毒的传染性极强，某地因1人患了甲型H1N1流感没有及时隔离治疗，经过两天传染后共有9人患了甲型H1N1流感，每天传染中平均一个人传染了几个人？如果按照这个传染速度，再经过5天的传染后，这个地区一共将会有多少人患甲型H1N1流感？‎ 累计确诊病例人数 新增病例人数 ‎0‎ ‎4‎ ‎21‎ ‎96‎ ‎163‎ ‎193‎ ‎267‎ ‎17‎ ‎75‎ ‎67‎ ‎30‎ ‎74‎ ‎16‎ ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ 日本‎2009年5月16日至‎5月21日 甲型H1N1流感疫情数据统计图 人数(人)‎ ‎0‎ ‎50‎ ‎100‎ ‎150‎ ‎200‎ ‎250‎ ‎300‎ 日期 A2‎ ‎9.（2009年益阳市）阅读材料：‎ 如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法：，即三角形面积等于水平宽与铅垂高乘积的一半.‎ B C 铅垂高 水平宽 h ‎ a ‎ ‎ ‎ x C O y A B D ‎1‎ ‎1‎ ‎ 解答下列问题：‎ 如图2，抛物线顶点坐标为点C(1,4),交x轴于点A(3,0)，交y轴于点B.‎ ‎（1）求抛物线和直线AB的解析式；‎ ‎（2）点P是抛物线(在第一象限内)上的一个动点，连结PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及；‎ ‎ （3）是否存在一点P，使S△PAB=S△CAB，若存在，求出P点的坐标；若不存在，请说明理由.‎ ‎10.（2009年济宁市）阅读下面的材料：‎ ‎ 在平面几何中，我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线，给出它们平行的定义：设一次函数的图象为直线，一次函数的图象为直线，若，且，我们就称直线与直线互相平行. ‎ ‎ 解答下面的问题：‎ ‎ （1）求过点且与已知直线平行的直线的函数表达式,并画出直线 的图象；‎ ‎ （2）设直线分别与轴、轴交于点、，如果直线：与直线平行且交轴于点，求出△的面积关于的函数表达式.‎ ‎2‎ ‎4‎ ‎6‎ ‎2‎ ‎4‎ ‎6‎ ‎－2‎ ‎－2‎ ‎11．(2009年湖州)若P为所在平面上一点，且，则点叫做的费马点.‎ ‎（1）若点为锐角的费马点，且，则的值为________；‎ ‎（2）如图，在锐角外侧作等边′连结′.‎ 求证：′过的费马点，且′=.‎ A C B ‎ ‎ ‎12.(2009年河北)如图1至图5，⊙O均作无滑动滚动，⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置，⊙O的周长为c．‎ 阅读理解：‎ 图1‎ A O1‎ O O2‎ B B 图2‎ A ‎ C n°‎ D O1‎ O2‎ B 图3‎ O2‎ O3‎ O A ‎ O1‎ C O4‎ ‎ O A B C 图4‎ D ‎D 图5‎ O ‎（1）如图1，⊙O从⊙O1的位置出发，沿AB滚动到⊙O2的位置，当AB = c时，⊙O恰好自转1周．‎ ‎（2）如图2，∠ABC相邻的补角是n°，⊙O在∠ABC外部沿A-B-C滚动，在点B处，必须由⊙O1的位置旋转到⊙O2的位置，⊙O绕点B旋转的角∠O1BO2 = n°，⊙O在点B处自转周．‎ 实践应用：‎ ‎（1）在阅读理解的（1）中，若AB = ‎2c，则⊙O自转 周；若AB = l，则⊙O自转 周．在阅读理解的（2）中，若∠ABC = 120°，则⊙O在点B处自转 周；若∠ABC = 60°，则⊙O在点B处自转 周．‎ ‎（2）如图3，∠ABC=90°，AB=BC=c．⊙O从⊙O1的位置出发，在∠ABC外部沿A-B-C滚动到⊙O4的位置，⊙O自转 周．‎ 拓展联想：‎ ‎（1）如图4，△ABC的周长为l，⊙O从与AB相切于点D的位置出发，在△ABC外部，按顺时针方向沿三角形滚动，又回到与AB相切于点D的位置，⊙O自转了多少周？请说明理由．‎ ‎（2）如图5，点D的位置出发，在多边形外部，按顺时针方向沿多边形滚动，又回到与该边相切于点D的位置，直接写出⊙O自转的周数．‎ ‎13.(2009年咸宁市)问题背景：‎ 在中，、、三边的长分别为、、，求这个三角形的面积．‎ 小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点（即三个顶点都在小正方形的顶点处），如图所示．这样不需求的高，而借用网格就能计算出它的面积．‎ ‎（1）请你将的面积直接填写在横线上．__________________‎ 思维拓展：‎ ‎（2）我们把上述求面积的方法叫做构图法．若三边的长分别为、、（），请利用图的正方形网格（每个小正方形的边长为）画出相应的，并求出它的面积．‎ 探索创新：‎ ‎（3）若三边的长分别为、、（，且），试运用构图法求出这三角形的面积．‎ ‎（图①）‎ ‎（图②）‎ A C B ‎14．（湖南邵阳）阅读下列材料，然后回答问题．‎ 在进行二次根式运算时，我们有时会碰上如一样的式子，其实我们还可以将其进一步化简：‎ ‎； （Ⅰ）‎ ‎ （Ⅱ）‎ ‎． （Ⅲ）‎ 以上这种化简的步骤叫做分母有理化．‎ 还可以用以下方法化简：‎ ‎． （Ⅳ）‎ ‎（1）请用不同的方法化简．‎ ‎①参照（Ⅲ）式得=___________________________________________．‎ ‎②参照（Ⅳ）式得=___________________________________________．‎ ‎（2）化简：．‎ ‎15．（09湖北宜昌）【实际背景】 ‎ 预警方案确定:‎ 设．如果当月W<6，则下个月要采取措施防止“猪贱伤农”． ‎ ‎【数据收集】 ‎ 今年2月～5月玉米、猪肉价格统计表 ‎ 月 份 ‎2‎ ‎3‎ ‎4‎ ‎5‎ 玉米价格(元/‎500克)‎ ‎0.7‎ ‎0.8‎ ‎0.9‎ ‎1‎ 猪肉价格(元/‎ ‎7.5‎ m ‎6.25‎ ‎6‎ ‎500克‎)‎ ‎【问题解决】‎ ‎(1)若今年3月的猪肉价格比上月下降的百分数与5月的猪肉价格比上月下降的百分数相等，求3月的猪肉价格m；‎ ‎(2)若今年6月及以后月份，玉米价格增长的规律不变，而每月的猪肉价格按照5月的猪肉价格比上月下降的百分数继续下降，请你预测7月时是否要采取措施防止“猪贱伤农”；‎ ‎(3)若今年6月及以后月份，每月玉米价格增长率是当月猪肉价格增长率的2倍，而每月的猪肉价格增长率都为a，则到7月时只用5.5元就可以买到‎500克猪肉和‎500克玉米．请你预测8月时是否要采取措施防止“猪贱伤农”． ‎ ‎16.（2009 黑龙江大兴安岭）已知：在中，，动点绕的顶点逆时针旋转，且，连结．过、的中点、作直线，直线与直线、分别相交于点、．‎ 图2‎ 图3‎ 图1‎ ‎(N)‎ ‎（1）如图1，当点旋转到的延长线上时，点恰好与点重合，取的中点，连结、，根据三角形中位线定理和平行线的性质，可得结论（不需证明）．‎ ‎（2）当点旋转到图2或图3中的位置时，与有何数量关系？请分别写出猜想，并任选一种情况证明．‎