九年级数学下册第一章直角三角形的边角关系1从梯子的倾斜程度谈起第2课时课件北师大版 21页

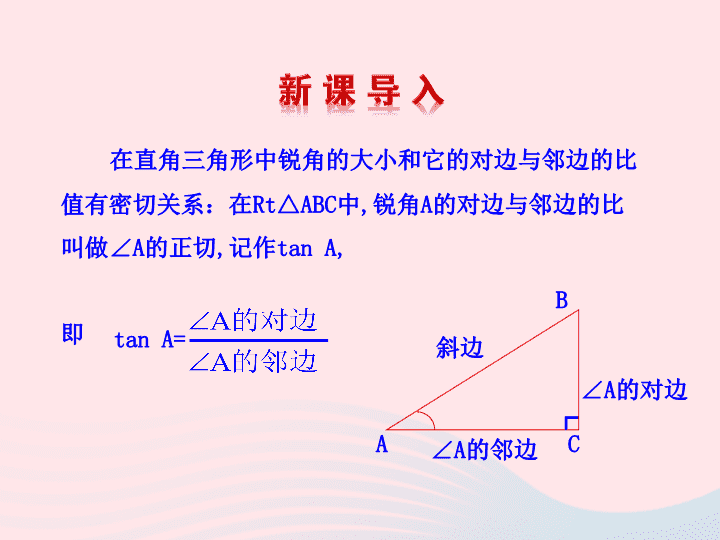
1 从梯子的倾斜 程度谈起 第 2 课时 1. 经历探索直角三角形中边角关系的过程，理解正弦和余弦的意义 .         2. 能够运用 sin A ， cos A 表示直角三角形两边的比 . 3. 能根据直角三角形中的边角关系进行简单的计算 . 4. 理解锐角三角函数的意义 . 在直角三角形中锐角的大小和它的对边与邻边的比值有密切关系： 在 Rt△ABC 中 , 锐角 A 的对边与邻边的比 叫做∠ A 的正切 , 记作 tan A, 即 tan A= A B C ∠A 的对边 ∠A 的邻边 ┌ 斜边 如图 , 当 Rt△ABC 中的一个锐角 A 确定时 , 你能找出哪些边之间的比值也确定吗 ? 【 结论 】 在 Rt△ABC 中 , 如果锐角 A 确定 , 那么∠ A 的对边与斜边的比 , ∠ A 的邻边与斜边的比也随之确定 . B ┌ 斜边 A C ∠A 的对边 ∠A 的邻边 【 定义 】 1. 在 Rt△ABC 中 , 锐角 A 的对边与斜边的比叫做∠ A 的正弦 , 记作 sin A, 即 . 2. 在 Rt△ABC 中 , 锐角 A 的邻边与斜边 的比叫做∠ A 的余弦 , 记作 cos A, 即 锐角 A 的正弦、余弦和正切都是∠ A 的三角函数 . A B C ∠A 的对边 ∠A 的邻边 ┌ 斜边 cos A= 斜边 Ð A 的邻边 sin A= 【 结论 】 梯子的倾斜程度与 sin A 和 cos A 有关 : cos A 的值越小，梯子越陡 . sin A 的值越大，梯子越陡； 如图 , 梯子的倾斜程度与 sin A 和 cos A 有关吗 ? 例 1. 如图，在 Rt△ABC 中 ,∠B=90°,AC=200,sin A=0.6. 求 BC 的长 . 请你求出 cos A,tan A,sin C,cos C 和 tan C 的值 . 你敢应战吗 ? 200 A C B ┌ 【 解析 】 在Rt△ABC中 【 例题 】 【 解析 】 cos A= tan A= cos C= sin C= tan C= 例 2. 如图:在Rt△ABC中,∠ C=90 ° ,AC=10 , 求AB,sinB. 你发现了什么？ 在直角三角形中，一个锐角的正弦等于另一个锐角的余弦 . A B C 1. 如图 : 在等腰三角形 ABC 中 ,AB=AC=5,BC=6. 求 : sin B,cos B,tan B. 温馨提示 : 过点 A 作 AD 垂直 BC 于点 D. 构造直角三角形 . 5 5 6 A B C D 【 跟踪训练 】 【 解析 】 过点 A 作 AD 垂直 BC 于点 D ，则 BD=CD=3 ，根据勾股定理得 AD=4 ， sin B= cos B= tan B= 2. 如图 , 在 Rt△ABC 中 , 锐角 A 的对边和邻边同时扩大 100 倍 ,sin A 的值（ ） A. 扩大 100 倍 B. 缩小 100 倍 C. 不变 D. 不能确定 3 .已知∠A,∠B为锐角 (1)若∠A=∠B,则sin A sin B . (2)若sin A=sin B,则∠A ∠B. A B C ┌ C = = 4. 如图 , ∠ACB=90° ， CD⊥AB. 若BD=6 , CD=12.求cos A的值. A C B D 【 解析 】 cosA= 1. （温州 · 中考）如图，在△ ABC 中， ∠ C=90°, AB=13 ， BC=5 ，则 sin A 的值是（ ） A. B. C. D. 【 解析 】 选 A ．由正弦的定义可得． A C B 2 ．（常德 · 中考）在 Rt△ABC 中 ,∠C=90°, 若 AC=2BC, 则 sin A 的值是 ( ) B ． 2 D ． 【 解析 】 选 C. A ． C ． 3 ．（三明 · 中考）如图，在梯形 ABCD 中， AD//BC ， AC⊥AB ， AD=CD ， ， BC=10 ，则 AB 的值 是（ ） A ． 9 B ． 8 C ． 6 D ． 3 【 解析 】 选 C. 4 ．（毕节 · 中考） 在正方形网格中，△ ABC 的位置如图所示，则 的值为（ ） A ． B ． C ． D ． 【 解析 】 选 B. 5 ．（建设兵团 · 中考） 如图（ 1 ）是一张 Rt△ABC 纸片，如果用两张相同的这种纸片恰好能拼成一个等边三角形，如图（ 2 ），那么在 Rt△ABC 中， sin B 的值是（ ） B. C. 1 D. 【 解析 】 选 B. A. 【 规律方法 】 在定义中应该注意的几个问题: (1) sin A,cos A,tan A 是在直角三角形中定义的,∠A 是锐角 (注意数形结合,构造直角三角形) . (2)sin A,cos A,tan A 是三个完整的符号,表示∠A 的 正弦 , 余弦 , 正切,习惯省去“∠”这个符 号 . (3)sin A,cos A,tan A 都是比值.注意比的顺序,且sin A, cos A,tan A 均大于0,无单位. (4)sin A,cos A,tan A 的值 只与∠ A的大小有关,而与直角三角形的边长无关. (5) 角相等,则其三角函数值相等；两锐角的同一三角函数值相等,则这两个锐角相等. 1. 锐角三角函数定义 : A B C ∠A 的对边 ∠A 的邻边 ┌ 斜边 sin A= cos A= 在直角三角形中，一个锐角的正弦等于另一个锐角的余弦 . 2. 在Rt△ABC中, sin A=cos B. tan A= ÐA 的对边 ÐA 的邻边 本来无望的事，大胆尝试，往往能成功 . —— 莎士比亚