北京市2008-2019年中考数学分类汇编统计与概率pdf含解析 47页

第 1页（共 47页） 2008～2019 北京中考数学分类汇编(统计与概率) 一．选择题（共 21 小题） 1．某校共有 200 名学生，为了解本学期学生参加公益劳动的情况，收集了他们参加公益劳 动时间（单位：小时）等数据，以下是根据数据绘制的统计图表的一部分 时间 t 人数 学生类型 0≤t＜10 10≤t＜20 20≤t＜30 30≤t＜40 t≥40 性别 男 7 31 25 30 4 女 8 29 26 32 8 学段 初中 25 36 44 11 高中 下面有四个推断： ① 这 200 名学生参加公益劳动时间的平均数一定在 24.5﹣25.5 之间 ② 这 200 名学生参加公益劳动时间的中位数在 20﹣30 之间 ③ 这 200 名学生中的初中生参加公益劳动时间的中位数一定在 20～30 之间 ④ 这 200 名学生中的高中生参加公益劳动时间的中位数可能在 20～30 之间 所有合理推断的序号是（ ） A． ①③ B． ②④ C． ①②③ D． 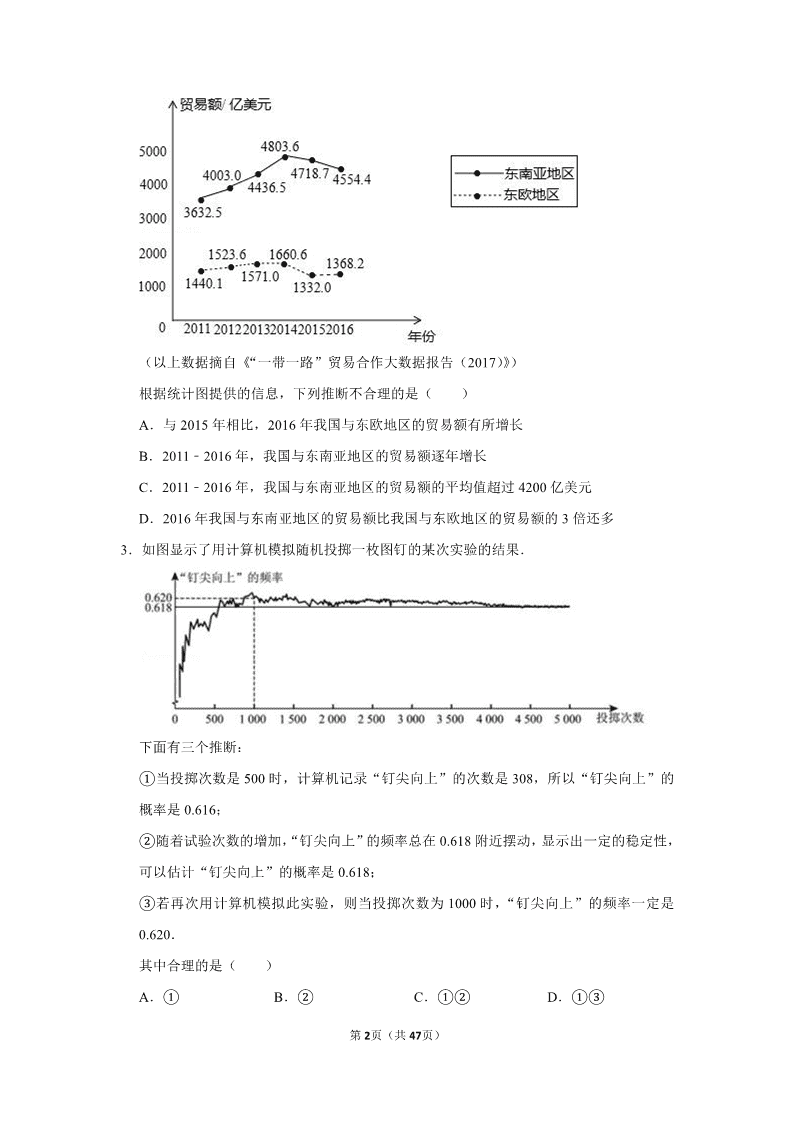①②③④2．下面的统计图反映了我国与“一带一路”沿线部分地区的贸易情况． 2011﹣2016 年我国与东南亚地区和东欧地区的贸易额统计图 第 2页（共 47页） （以上数据摘自《“一带一路”贸易合作大数据报告（2017）》） 根据统计图提供的信息，下列推断不合理的是（ ） A．与 2015 年相比，2016 年我国与东欧地区的贸易额有所增长 B．2011﹣2016 年，我国与东南亚地区的贸易额逐年增长 C．2011﹣2016 年，我国与东南亚地区的贸易额的平均值超过 4200 亿美元 D．2016 年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的 3 倍还多 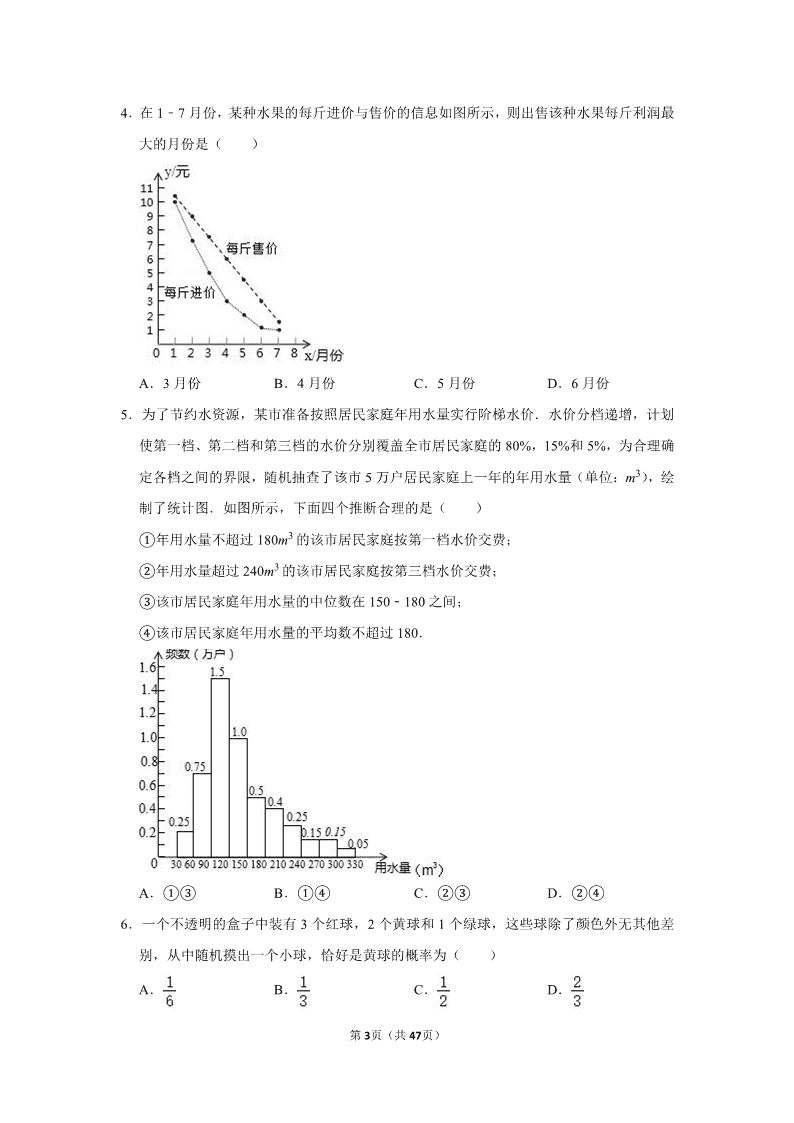3．如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果． 下面有三个推断： ① 当投掷次数是 500 时，计算机记录“钉尖向上”的次数是 308，所以“钉尖向上”的 概率是 0.616； ② 随着试验次数的增加，“钉尖向上”的频率总在 0.618 附近摆动，显示出一定的稳定性， 可以估计“钉尖向上”的概率是 0.618； ③ 若再次用计算机模拟此实验，则当投掷次数为 1000 时，“钉尖向上”的频率一定是 0.620． 其中合理的是（ ） A． ① B． ② C． ①② D． ①③ 第 3页（共 47页） 4．在 1﹣7 月份，某种水果的每斤进价与售价的信息如图所示，则出售该种水果每斤利润最 大的月份是（ ） A．3 月份 B．4 月份 C．5 月份 D．6 月份 5．为了节约水资源，某市准备按照居民家庭年用水量实行阶梯水价．水价分档递增，计划 使第一档、第二档和第三档的水价分别覆盖全市居民家庭的 80%，15%和 5%，为合理确 定各档之间的界限，随机抽查了该市 5 万户居民家庭上一年的年用水量（单位：m3），绘 制了统计图．如图所示，下面四个推断合理的是（ ） ① 年用水量不超过 180m3 的该市居民家庭按第一档水价交费； ② 年用水量超过 240m3 的该市居民家庭按第三档水价交费； ③ 该市居民家庭年用水量的中位数在 150﹣180 之间； ④ 该市居民家庭年用水量的平均数不超过 180． A． ①③ B． ①④ C． ②③ D． ②④6．一个不透明的盒子中装有 3 个红球，2 个黄球和 1 个绿球，这些球除了颜色外无其他差 别，从中随机摸出一个小球，恰好是黄球的概率为（ ） A． B． C． D． 第 4页（共 47页） 7．某市 6 月份日平均气温统计如图所示，则在日平均气温这组数据中，众数和中位数分别 是（ ） A．21，21 B．21，21.5 C．21，22 D．22，22 8．如图，有 6 张扑克牌，从中随机抽取一张，点数为偶数的概率是（ ） A． B． C． D． 9．某篮球队 12 名队员的年龄如表： 年龄（岁） 18 19 20 21 人数 5 4 1 2 则这 12 名队员年龄的众数和平均数分别是（ ） A．18，19 B．19，19 C．18，19.5 D．19，19.5 10．在一个不透明的口袋中装有 5 个完全相同的小球，把它们分别标号为 1，2，3，4，5， 从中随机摸出一个小球，其标号大于 2 的概率为（ ） A． B． C． D． 11．某中学随机地调查了 50 名学生，了解他们一周在校的体育锻炼时间，结果如下表所示： 时间（小时） 5 6 7 8 人数 10 15 20 5 则这 50 名学生这一周在校的平均体育锻炼时间是（ ） A．6.2 小时 B．6.4 小时 C．6.5 小时 D．7 小时 第 5页（共 47页） 12．班主任王老师将 6 份奖品分别放在 6 个完全相同的不透明礼盒中，准备将它们奖给小英 等 6 位获“爱集体标兵”称号的同学．这些奖品中 3 份是学习文具，2 份是科普读物，1 份是科技馆通票．小英从中随机抽取一份奖品，恰好取到科普读物的概率是（ ） A． B． C． D． 13．某课外小组的同学们在社会实践活动中调查了 20 户家庭某月的用电量，如表所示： 用电量（度） 120 140 160 180 200 户数 2 3 6 7 2 则这 20 户家庭该月用电量的众数和中位数分别是（ ） A．180，160 B．160，180 C．160，160 D．180，180 14．北京今年 6 月某日部分区县的高气温如下表： 区县 大兴 通州 平谷 顺义 怀柔 门头沟 延庆 昌平 密云 房山 最高气温 32 32 30 32 30 32 29 32 30 32 则这 10 个区县该日最高气温的众数和中位数分别是（ ） A．32，32 B．32，30 C．30，32 D．32，31 15．一个不透明的盒子中装有 2 个白球，5 个红球和 8 个黄球，这些球除颜色外，没有任何 其他区别，现从这个盒子中随机摸出一个球，摸到红球的概率为（ ） A． B． C． D． 16．从：1、2、3、4、5、6、7、8、9、10 这十个数中随机取出一个数，取出的数是 3 的倍 数的概率是（ ） A． B． C． D． 17．10 名同学分成甲、乙两队进行篮球比赛，它们的身高（单位：cm）如下表所示： 队员 1 队员 2 队员 3 队员 4 队员 5 甲队 177 176 175 172 175 乙队 170 175 173 174 183 设两队队员身高的平均数依次为 甲， 乙，身高的方差依次为 S 甲 2，S 乙 2，则下列关系中 完全正确的是（ ） A． 甲＝ 乙，S 甲 2＞S 乙 2 B． 甲＝ 乙，S 甲 2＜S 乙 2 第 6页（共 47页） C． 甲＞ 乙，S 甲 2＞S 乙 2 D． 甲＜ 乙，S 甲 2＜S 乙 2 18．某班共有 41 名同学，其中有 2 名同学习惯用左手写字，其余同学都习惯用右手写字， 老师随机请 1 名同学解答问题，习惯用左手写字的同学被选中的概率是（ ） A．0 B． C． D．1 19．某班派 9 名同学参加拔河比赛，他们的体重分别是（单位：千克）：67、59、61、59、 63、57、70、59、65，这组数据的众数和中位数分别是（ ） A．59，63 B．59，61 C．59，59 D．57，61 20．众志成城，抗震救灾．某小组 7 名同学积极捐出自己的零花钱支援灾区，他们捐款的数 额分别是（单位/元）：50，20，50，30，50，25，135．这组数据的众数和中位数分别是 （ ） A．50，20 B．50，30 C．50，50 D．135，50 21．如图，有 5 张形状、大小、质地均相同的卡片，正面分别印有北京奥运会的会徽、吉祥 物（福娃）、火炬和奖牌等四种不同的图案，背面完全相同．现将这 5 张卡片洗匀后正面 向下放在桌子上，从中随机抽取一张，抽出的卡片正面图案恰好是吉祥物（福娃）的概 率是（ ） A． B． C． D． 二．填空题（共 4 小题） 22．小天想要计算一组数据 92，90，94，86，99，85 的方差 s02，在计算平均数的过程中， 将这组数据中的每一个数都减去 90，得到一组新数据 2，0，4，﹣4，9，﹣5，记这组新 数据的方差为 s12，则 s12 s02（填“＞”，“＝”或”＜”） 23．从甲地到乙地有 A，B，C 三条不同的公交线路．为了解早高峰期间这三条线路上的公 交车从甲地到乙地的用时情况，在每条线路上随机选取了 500 个班次的公交车，收集了 这些班次的公交车用时（单位：分钟）的数据，统计如下： 公交车用时 公交车用时的频数 线路 30≤t≤35 35＜t≤40 40＜t≤45 45＜t≤50 合计 第 7页（共 47页） A 59 151 166 124 500 B 50 50 122 278 500 C 45 265 167 23 500 早高峰期间，乘坐 （填“A”，“B”或“C”）线路上的公交车，从甲地到乙地“用 时不超过 45 分钟”的可能性最大． 24．林业部门要考察某种幼树在一定条件下的移植成活率，下表是这种幼树在移植过程中的 一组数据： 移植的 棵数 n 1000 1500 2500 4000 8000 15000 20000 30000 成活的 棵数 m 865 1356 2220 3500 7056 13170 17580 26430 成活的 频率 0.865 0.904 0.888 0.875 0.882 0.878 0.879 0.881 估计该种幼树在此条件下移植成活的概率为 ． 25．北京市 2009﹣2014 年轨道交通日均客运量统计如图所示．根据统计图中提供的信息， 预估 2015 年北京市轨道交通日均客运量约 万人次，你的预估理由是 ． 三．解答题（共 12 小题） 26．国家创新指数是反映一个国家科学技术和创新竞争力的综合指数．对国家创新指数得分 排名前 40 的国家的有关数据进行收集、整理、描述和分析．下面给出了部分信息： a．国家创新指数得分的频数分布直方图（数据分成 7 组：30≤x＜40，40≤x＜50，50≤ x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）； 第 8页（共 47页） b．国家创新指数得分在 60≤x＜70 这一组的是： 61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5 c．40 个国家的人均国内生产总值和国家创新指数得分情况统计图： d．中国的国家创新指数得分为 69.5． （以上数据来源于《国家创新指数报告（2018）》） 根据以上信息，回答下列问题： （1）中国的国家创新指数得分排名世界第 ； （2）在 40 个国家的人均国内生产总值和国家创新指数得分情况统计图中，包括中国在 内的少数几个国家所对应的点位于虚线 l1 的上方，请在图中用“〇”圈出代表中国的点； （3）在国家创新指数得分比中国高的国家中，人均国内生产总值的最小值约为 万 美元；（结果保留一位小数） （4）下列推断合理的是 ． ① 相比于点 A，B 所代表的国家，中国的国家创新指数得分还有一定差距，中国提出“加 快建设创新型国家”的战略任务，进一步提高国家综合创新能力； ② 相比于点 B，C 所代表的国家，中国的人均国内生产总值还有一定差距，中国提出“决 胜全面建成小康社会”的奋斗目标，进一步提高人均国内生产总值． 第 9页（共 47页） 27．某年级共有 300 名学生．为了解该年级学生 A，B 两门课程的学习情况，从中随机抽取 60 名学生进行测试，获得了他们的成绩（百分制），并对数据（成绩）进行整理、描述和 分析．下面给出了部分信息． a．A 课程成绩的频数分布直方图如下（数据分成 6 组：40≤x＜50，50≤x＜60，60≤x ＜70，70≤x＜80，80≤x＜90，90≤x≤100）： b．A 课程成绩在 70≤x＜80 这一组的是：70 71 71 71 76 76 77 78 78.5 78.5 79 79 79 79.5 c．A，B 两门课程成绩的平均数、中位数、众数如下： 课程 平均数 中位数 众数 A 75.8 m 84.5 B 72.2 70 83 根据以上信息，回答下列问题： （1）写出表中 m 的值； （2）在此次测试中，某学生的 A 课程成绩为 76 分，B 课程成绩为 71 分，这名学生成绩 排名更靠前的课程是 （填“A“或“B“），理由是 ， （3）假设该年级学生都参加此次测试，估计 A 课程成绩超过 75.8 分的人数． 28．某工厂甲、乙两个部门各有员工 400 人，为了解这两个部门员工的生产技能情况，进行 了抽样调查，过程如下，请补充完整． 收集数据 从甲、乙两个部门各随机抽取 20 名员工，进行了生产技能测试，测试成绩（百分制）如 下： 甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77 第 10页（共 47页） 乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40 整理、描述数据 按如下分数段整理、描述这两组样本数据： 成绩 x 人数 部门 40≤x≤49 50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤ 100 甲 0 0 1 11 7 1 乙 （说明：成绩 80 分及以上为生产技能优秀，70﹣﹣79 分为生产技能良好，60﹣﹣69 分 为生产技能合格，60 分以下为生产技能不合格） 分析数据 两组样本数据的平均数、中位数、众数如下表所示： 部门 平均数 中位数 众数 甲 78.3 77.5 75 乙 78 80.5 81 得出结论：a．估计乙部门生产技能优秀的员工人数为 ；b．可以推断出 部 门员工的生产技能水平较高，理由为 ．（至少从两个不同的角度说明推断的合理 性） 29．调查作业：了解你所在小区家庭 5 月份用气量情况： 小天、小东和小芸三位同学住在同一小区，该小区共有 300 户家庭，每户家庭人数在 2 ﹣5 之间，这 300 户家庭的平均人数约为 3.4． 小天、小东和小芸各自对该小区家庭 5 月份用气量情况进行了抽样调查，将收集的数据 进行了整理，绘制的统计表分别为表 1，表 2 和表 3． 表 1 抽样调查小区 4 户家庭 5 月份用气量统计表 （单位：m3） 家庭人数 2 3 4 5 用气量 14 19 21 26 表 2 抽样调查小区 15 户家庭 5 月份用气量统计表 （单位：m3） 第 11页（共 47页） 家庭 人数 2 2 2 3 3 3 3 3 3 3 3 3 3 3 4 用气 量 10 11 15 13 14 15 15 17 17 18 18 18 18 20 22 表 3 抽样调查小区 15 户家庭 5 月份用气量统计表 （单位：m3） 家庭 人数 2 2 3 3 3 3 3 3 3 4 4 4 4 5 5 用气 量 10 12 13 14 17 17 18 19 20 20 22 26 31 28 31 根据以上材料回答问题： 小天、小东和小芸三人中，哪一位同学抽样调查的数据能较好地反映该小区家庭 5 月份 用气量情况，并简要说明其他两位同学抽样调查的不足之处． 30．阅读下列材料： 2015 年清明小长假，北京市属公园开展以“清明踏青，春色满园”为主题的游园活动， 虽然气温小幅走低，但游客踏青赏花的热情很高，市属公园游客接待量约为190万人次．其 中，玉渊潭公园的樱花、北京植物园的桃花受到了游客的热捧，两公园的游客接待量分 别为 38 万人次、21.75 万人次；颐和园、天坛公园、北海公园因皇家园林的厚重文化底 蕴与满园春色成为游客的重要目的地，游客接待量分别为 26 万人次、20 万人次、17.6 万人次；北京动物园游客接待量为 18 万人次，熊猫馆的游客密集度较高． 2014 年清明小长假，天气晴好，北京市属公园游客接待量约为 200 万人次，其中，玉渊 潭公园游客接待量比 2013 年清明小长假增长了 25%；颐和园游客接待量为 26.2 万人次， 比 2013 年清明小长假增加了 4.6 万人次；北京动物园游客接待量为 22 万人次． 2013 年清明小长假，玉渊潭公园、陶然亭公园、北京动物园游客接待量分别为 32 万人次、 13 万人次、14.9 万人次． 根据以上材料解答下列问题： （1）2014 年清明小长假，玉渊潭公园游客接待量为 万人次； （2）选择统计表或统计图，将 2013﹣2015 年清明小长假玉渊潭公园、颐和园和北京动 物园的游客接待量表示出来． 31．根据某研究院公布的 2009～2013 年我国成年国民阅读调查报告的部分相关数据，绘制 第 12页（共 47页） 的统计图表如下： 2009～2013 年成年国民 年人均阅读图书数量统计表 年份 年人均阅读图书数 量（本） 2009 3.88 2010 4.12 2011 4.35 2012 4.56 2013 4.78 根据以上信息解答下列问题： （1）直接写出扇形统计图中 m 的值； （2）从 2009 到 2013 年，成年国民年人均阅读图书的数量每年增长的幅度近似相等，估 算 2014 年成年国民年人均阅读图书的数量约为 本； （3）2013 年某小区倾向图书阅读的成年国民有 990 人，若该小区 2014 年与 2013 年成年 国民的人数基本持平，估算 2014 年该小区成年国民阅读图书的总数量约为 本． 32．第九届中国国际园林博览会（园博会）已于 2013 年 5 月 18 日在北京开幕，以下是根据 近几届园博会的相关数据绘制的统计图的一部分． 第 13页（共 47页） （1）第九届园博会的植物花园区由五个花园组成，其中月季园面积为 0.04 平方千米，牡 丹园面积为 平方千米； （2）第九届园博会会园区陆地面积是植物花园区总面积的 18 倍，水面面积是第七、八 界园博会的水面面积之和，请根据上述信息补全条形统计图，并标明相应数据； （3）小娜收集了几届园博会的相关信息（如下表），发现园博会园区周边设置的停车位 数量与日均接待游客量和单日最多接待游客量中的某个量近似成正比例关系．根据小娜 的发现，请估计，将于 2015 年举办的第十届园博会大约需要设置的停车位数量（直接写 出结果，精确到百位）． 第七届至第十届园博会游客量和停车位数量统计表： 日接待游客量 （万人次） 单日最多接待游客量 （万人次） 停车位数量 （个） 第七届 0.8 6 约 3000 第八届 2.3 8.2 约 4000 第九届 8（预计） 20（预计） 约 10500 第十届 1.9（预计） 7.4（预计） 约 33．近年来，北京市大力发展轨道交通，轨道运营里程大幅增加，2011 年北京市又调整修 订了 2010 至 2020 年轨道交通线网的发展规划．以下是根据北京市轨道交通指挥中心发 布的有关数据制作的统计图表的一部分． 北京市轨道交通已开通线路相关数据统计表（截止 2010 年底） 开通时间 开通线路 运营里程（千米） 第 14页（共 47页） 1971 1 号线 31 1984 2 号线 23 2003 13 号线 41 八通线 19 2007 5 号线 28 2008 8 号线 5 10 号线 25 机场线 28 2009 4 号线 28 2010 房山线 22 大兴线 22 亦庄线 23 昌平线 21 15 号线 20 请根据以上信息解答下列问题： （1）补全条形统计图并在图中标明相应数据； （2）按照 2011 年规划方案，预计 2020 年北京市轨道交通运营总里程将达到多少千米？ （3）要按时完成截至 2015 年的轨道交通规划任务，从 2011 到 2015 年这 4 年中，平均 每年需新增运营里程多少千米？ 第 15页（共 47页） 34．以下是根据北京市国民经济和社会发展统计公报中的相关数据，绘制统计图的一部分． 请根据以上信息解答下列问题： （1）2008 年北京市私人轿车拥有是多少万辆（结果保留三个有效数字）？ （2）补全条形统计图； （3）汽车数量增多除造成交通拥堵外，还增加了碳排放量，为了了解汽车碳排放量的情 况，小明同学通过网络了解到汽车的碳排放量与汽车排量有关．如：一辆排量为 1.6L 的 轿车，如果一年行驶 1 万千米，这一年，它碳排放量约为 2.7 吨．于是他调查了他所居住 小区的 150 辆私人轿车，不同排量的轿车数量如下表所示． 排量（L） 小于 1.6 1.6 1.8 大于 1.8 数量（辆） 29 75 31 15 如果按照小明的统计数据，请你通过计算估计，2010 年北京市仅排量为 1.6L 的这类私人 第 16页（共 47页） 轿车（假设每辆车平均一行行驶 1 万千米）的碳排放总量约为多少万吨？ 35．根据北京市统计局的 2006﹣2009 年空气质量的相关数据，绘制统计图如下： （1）由统计图中的信息可知，北京全年市区空气质量达到二级和好于二级的天数与上一 年相比，增加最多的是 年，增加了 天； （2）表 1 是根据《中国环境发展报告（2010）》公布的数据绘制的 2009 年十个城市供气 质量达到二级和好于二级的天数占全年天数百分比的统计表，请将表 1 中的空缺部分补 充完整（精确到 1%）． 2009 年十个城市空气质量达到二级和好于二级的天数占全年天数百分比统计表：3 城市 北京 上海 天津 昆明 杭州 广州 南京 成都 沈阳 西宁 百分比 91% 84% 100% 89% 95% 86% 86% 90% 77% （3）根据表 1 中的数据将十个城市划分为三个组，百分比不低于 95%的为 A 组，不低于 85%且低于 95%的为 B 组，低于 85%的为 C 组．按此标准，C 组城市数量在这十个城市 中所占的百分比为 %；请你补全右边的扇形统计图． 36．在每年年初召开的市人代会上，北京市财政局都要报告上一年度市财政预算执行情况和 当年预算情况．以下是根据 2004﹣2008 年度报告中的有关数据制作的市财政教育预算与 实际投入统计图表的一部分． 2004﹣2008 年北京市财政教育实际投入与预算差值统计表（单位：亿元） 年份 2004 2005 2006 2007 2008 第 17页（共 47页） 教育实际投 入与预算差值 6.7 5.7 14.6 7.3 请根据以上信息解答下列问题： （1）请在表 1 的空格内填入 2004 年市财政教育实际投入与预算的差值； （2）求 2004﹣2008 年北京市财政教育实际投入与预算差值的平均数； （3）已知 2009 年北京市财政教育预算是 141.7 亿元．在此基础上，如果 2009 年北京市 财政教育实际投入按照（2）中求出的平均数增长，估计它的金额可能达到多少亿元？ 37．为减少环境污染，自 2008 年 6 月 1 日起，全国的商品零售场所开始实行“塑料购物袋 有偿使用制度”（以下简称“限塑令”）．某班同学于 6 月上旬的一天，在某超市门口采用 问卷调查的方式，随机调查了“限塑令”实施前后，顾客在该超市用购物袋的情况，以 下是根据 100 位顾客的 100 份有效答卷画出的统计图表的一部分： “限塑令”实施后，塑料购物袋使用后的处理方式统计表： 处理方式 直接丢弃 直接做垃圾袋 再次购物使用 其它 选该项的人数占 5% 35% 49% 11% 第 18页（共 47页） 总人数的百分比 请你根据以上信息解答下列问题： （1）补全图 1，“限塑令”实施前，如果每天约有 2 000 人次到该超市购物．根据这 100 位顾客平均一次购物使用塑料购物袋的平均数，估计这个超市每天需要为顾客提供多少 个塑料购物袋？ （2）补全图 2，并根据统计图和统计表说明，购物时怎样选用购物袋，塑料购物袋使用 后怎样处理，能对环境保护带来积极的影响． 第 19页（共 47页） 2008～2019 北京中考数学分类汇编(统计与概率) 参考答案与试题解析 一．选择题（共 21 小题） 1．某校共有 200 名学生，为了解本学期学生参加公益劳动的情况，收集了他们参加公益劳 动时间（单位：小时）等数据，以下是根据数据绘制的统计图表的一部分 时间 t 人数 学生类型 0≤t＜10 10≤t＜20 20≤t＜30 30≤t＜40 t≥40 性别 男 7 31 25 30 4 女 8 29 26 32 8 学段 初中 25 36 44 11 高中 下面有四个推断： ① 这 200 名学生参加公益劳动时间的平均数一定在 24.5﹣25.5 之间 ② 这 200 名学生参加公益劳动时间的中位数在 20﹣30 之间 ③ 这 200 名学生中的初中生参加公益劳动时间的中位数一定在 20～30 之间 ④ 这 200 名学生中的高中生参加公益劳动时间的中位数可能在 20～30 之间 所有合理推断的序号是（ ） A． ①③ B． ②④ C． ①②③ D． ①②③④【解答】解： ① 解这 200 名学生参加公益劳动时间的平均数： ① （24.5×97+25.5×103） 第 20页（共 47页） ÷200＝25.015，一定在 24.5﹣25.5 之间，正确； ② 由统计表类别栏计算可得，各时间段人数分别为 15，60，51，62，12，则中位数在 20﹣30 之间，故 ② 正确． ③ 由统计表计算可得，初中学段栏 0≤t＜10 的人数在 0﹣15 之间，当人数为 0 时中位 数在 20﹣30 之间；当人数为 15 时，中位数在 20﹣30 之间，故 ③ 正确． ④ 由统计表计算可得，高中学段栏各时间段人数分别为 0﹣15，35，15，18，1，当 0≤ t＜10 时间段人数为 0 时，中位数在 10﹣20 之间；当 0≤t＜10 时间段人数为 15 时， 中位数在 10﹣20 之间，故 ④ 错误． 故选：C． 2．下面的统计图反映了我国与“一带一路”沿线部分地区的贸易情况． 2011﹣2016 年我国与东南亚地区和东欧地区的贸易额统计图 （以上数据摘自《“一带一路”贸易合作大数据报告（2017）》） 根据统计图提供的信息，下列推断不合理的是（ ） A．与 2015 年相比，2016 年我国与东欧地区的贸易额有所增长 B．2011﹣2016 年，我国与东南亚地区的贸易额逐年增长 C．2011﹣2016 年，我国与东南亚地区的贸易额的平均值超过 4200 亿美元 D．2016 年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的 3 倍还多 【解答】解：A、由折线统计图可得： 与 2015 年相比，2016 年我国与东欧地区的贸易额有所增长，正确，不合题意； B、由折线统计图可得：2011﹣2014 年，我国与东南亚地区的贸易额 2014 年后有所下降， 故逐年增长错误，故此选项错误，符合题意； C、2011﹣2016 年，我国与东南亚地区的贸易额的平均值为： 第 21页（共 47页） （3632.5+4003.0+4436.5+4803.6+4718.7+4554.4）÷6≈4358， 故超过 4200 亿美元，正确，不合题意， D、∵4554.4÷1368.2≈3.33， ∴2016 年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的 3 倍还多， 故选：B． 3．如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果． 下面有三个推断： ① 当投掷次数是 500 时，计算机记录“钉尖向上”的次数是 308，所以“钉尖向上”的 概率是 0.616； ② 随着试验次数的增加，“钉尖向上”的频率总在 0.618 附近摆动，显示出一定的稳定性， 可以估计“钉尖向上”的概率是 0.618； ③ 若再次用计算机模拟此实验，则当投掷次数为 1000 时，“钉尖向上”的频率一定是 0.620． 其中合理的是（ ） A． ① B． ② C． ①② D． ①③【解答】解：当投掷次数是 500 时，计算机记录“钉尖向上”的次数是 308，所以此时“钉 尖向上”的频率是：308÷500＝0.616，但“钉尖向上”的概率不一定是 0.616，故 ① 错 误， 随着实验次数的增加，“钉尖向上”的频率总在 0.618 附近摆动，显示出一定的稳定性， 可以估计“钉尖向上”的概率是 0.618．故 ② 正确， 若再次用计算机模拟实验，则当投掷次数为 1000 时，“钉尖向上”的概率可能是 0.620， 但不一定是 0.620，故 ③ 错误， 故选：B． 4．在 1﹣7 月份，某种水果的每斤进价与售价的信息如图所示，则出售该种水果每斤利润最 第 22页（共 47页） 大的月份是（ ） A．3 月份 B．4 月份 C．5 月份 D．6 月份 【解答】解：由图象中的信息可知，3 月份的利润＝7.5﹣5＝2.5 元， 4 月份的利润＝6﹣3＝3 元， 5 月份的利润＝4.5﹣2＝2.5 元， 6 月份的利润＝3﹣1.2＝1.8 元， 故出售该种水果每斤利润最大的月份是 4 月份， 故选：B． 5．为了节约水资源，某市准备按照居民家庭年用水量实行阶梯水价．水价分档递增，计划 使第一档、第二档和第三档的水价分别覆盖全市居民家庭的 80%，15%和 5%，为合理确 定各档之间的界限，随机抽查了该市 5 万户居民家庭上一年的年用水量（单位：m3），绘 制了统计图．如图所示，下面四个推断合理的是（ ） ① 年用水量不超过 180m3 的该市居民家庭按第一档水价交费； ② 年用水量超过 240m3 的该市居民家庭按第三档水价交费； ③ 该市居民家庭年用水量的中位数在 150﹣180 之间； ④ 该市居民家庭年用水量的平均数不超过 180． 第 23页（共 47页） A． ①③ B． ①④ C． ②③ D． ②④【解答】解： ① 由条形统计图可得：年用水量不超过 180m3 的该市居民家庭一共有 （0.25+0.75+1.5+1.0+0.5）＝4（万）， ×100%＝80%，故年用水量不超过 180m3 的该市居民家庭按第一档水价交费，正确； ② ∵年用水量超过 240m3 的该市居民家庭有（0.15+0.15+0.05）＝0.35（万）， ∴ ×100%＝7%≠5%，故年用水量超过 240m3 的该市居民家庭按第三档水价交费， 故此选项错误； ③ ∵5 万个数数据的中间是第 25000 和 25001 的平均数， ∴该市居民家庭年用水量的中位数在 120﹣150 之间，故此选项错误； ④ 由 ① 得，该市居民家庭年用水量的平均数不超过 180，正确， 故选：B． 6．一个不透明的盒子中装有 3 个红球，2 个黄球和 1 个绿球，这些球除了颜色外无其他差 别，从中随机摸出一个小球，恰好是黄球的概率为（ ） A． B． C． D． 【解答】解：从中随机摸出一个小球，恰好是黄球的概率＝ ＝ ． 故选：B． 7．某市 6 月份日平均气温统计如图所示，则在日平均气温这组数据中，众数和中位数分别 是（ ） 第 24页（共 47页） A．21，21 B．21，21.5 C．21，22 D．22，22 【解答】解：这组数据中，21 出现了 10 次，出现次数最多，所以众数为 21， 第 15 个数和第 16 个数都是 22，所以中位数是 22． 故选：C． 8．如图，有 6 张扑克牌，从中随机抽取一张，点数为偶数的概率是（ ） A． B． C． D． 【解答】解：∵有 6 张扑克牌，从中随机抽取一张，点数为偶数的有 3 种情况， ∴从中随机抽取一张，点数为偶数的概率是： ＝ ． 故选：D． 9．某篮球队 12 名队员的年龄如表： 年龄（岁） 18 19 20 21 人数 5 4 1 2 则这 12 名队员年龄的众数和平均数分别是（ ） A．18，19 B．19，19 C．18，19.5 D．19，19.5 【解答】解：年龄为 18 岁的队员人数最多，众数是 18； 平均数＝ ＝19． 故选：A． 10．在一个不透明的口袋中装有 5 个完全相同的小球，把它们分别标号为 1，2，3，4，5， 第 25页（共 47页） 从中随机摸出一个小球，其标号大于 2 的概率为（ ） A． B． C． D． 【解答】解：根据题意可得：大于 2 的有 3，4，5 三个球，共 5 个球， 任意摸出 1 个，摸到大于 2 的概率是 ． 故选：C． 11．某中学随机地调查了 50 名学生，了解他们一周在校的体育锻炼时间，结果如下表所示： 时间（小时） 5 6 7 8 人数 10 15 20 5 则这 50 名学生这一周在校的平均体育锻炼时间是（ ） A．6.2 小时 B．6.4 小时 C．6.5 小时 D．7 小时 【解答】解：根据题意得： （5×10+6×15+7×20+8×5）÷50 ＝（50+90+140+40）÷50 ＝320÷50 ＝6.4（小时）． 故这 50 名学生这一周在校的平均体育锻炼时间是 6.4 小时． 故选：B． 12．班主任王老师将 6 份奖品分别放在 6 个完全相同的不透明礼盒中，准备将它们奖给小英 等 6 位获“爱集体标兵”称号的同学．这些奖品中 3 份是学习文具，2 份是科普读物，1 份是科技馆通票．小英从中随机抽取一份奖品，恰好取到科普读物的概率是（ ） A． B． C． D． 【解答】解：从中随机抽取一份奖品，恰好取到科普读物的概率是 ＝ ． 故选：B． 13．某课外小组的同学们在社会实践活动中调查了 20 户家庭某月的用电量，如表所示： 用电量（度） 120 140 160 180 200 户数 2 3 6 7 2 则这 20 户家庭该月用电量的众数和中位数分别是（ ） A．180，160 B．160，180 C．160，160 D．180，180 第 26页（共 47页） 【解答】解：在这一组数据中 180 是出现次数最多的，故众数是 180； 将这组数据从小到大的顺序排列后，处于中间位置的两个数是 160，160，那么由中位数 的定义可知，这组数据的中位数是（160+160）÷2＝160． 故选：A． 14．北京今年 6 月某日部分区县的高气温如下表： 区县 大兴 通州 平谷 顺义 怀柔 门头沟 延庆 昌平 密云 房山 最高气温 32 32 30 32 30 32 29 32 30 32 则这 10 个区县该日最高气温的众数和中位数分别是（ ） A．32，32 B．32，30 C．30，32 D．32，31 【解答】解：在这一组数据中 32 是出现次数最多的，故众数是 32； 处于这组数据中间位置的数是 32、32，那么由中位数的定义可知，这组数据的中位数是 32． 故选：A． 15．一个不透明的盒子中装有 2 个白球，5 个红球和 8 个黄球，这些球除颜色外，没有任何 其他区别，现从这个盒子中随机摸出一个球，摸到红球的概率为（ ） A． B． C． D． 【解答】解：根据题意可得：一个不透明的盒子中装有 2 个白球，5 个红球和 8 个黄球， 共 15 个， 摸到红球的概率为 ＝ ， 故选：B． 16．从：1、2、3、4、5、6、7、8、9、10 这十个数中随机取出一个数，取出的数是 3 的倍 数的概率是（ ） A． B． C． D． 【解答】解：∵1、2、3、4、5、6、7、8、9、10 这十个数中，3 的倍数的有 3、6、9 共 3 个数， ∴取出的数是 3 的倍数的概率是： ． 故选：B． 17．10 名同学分成甲、乙两队进行篮球比赛，它们的身高（单位：cm）如下表所示： 第 27页（共 47页） 队员 1 队员 2 队员 3 队员 4 队员 5 甲队 177 176 175 172 175 乙队 170 175 173 174 183 设两队队员身高的平均数依次为 甲， 乙，身高的方差依次为 S 甲 2，S 乙 2，则下列关系中 完全正确的是（ ） A． 甲＝ 乙，S 甲 2＞S 乙 2 B． 甲＝ 乙，S 甲 2＜S 乙 2 C． 甲＞ 乙，S 甲 2＞S 乙 2 D． 甲＜ 乙，S 甲 2＜S 乙 2 【解答】解： 甲＝ （177+176+175+172+175）＝175， S 甲 2＝ [（177﹣175）2+（176﹣175）2+（175﹣175）2+（172﹣175）2+（175﹣175）2] ＝2.8． 乙＝ （170+175+173+174+183）＝175， S 乙 2＝ [（170﹣175）2+（175﹣175）2+（173﹣175）2+（174﹣175）2+（183﹣175）2] ＝18.8． 故选：B． 18．某班共有 41 名同学，其中有 2 名同学习惯用左手写字，其余同学都习惯用右手写字， 老师随机请 1 名同学解答问题，习惯用左手写字的同学被选中的概率是（ ） A．0 B． C． D．1 【解答】解：这个班上共有 41 名学生，其中有 2 名同学习惯用左手写字，因为每名学生 被选中的机会相等，所以班主任随机请一名学生解答问题，则用左手写字的学生被选中 的概率是 ； 抽到习惯用左手写字的情况有两个可能，随机抽取时有 41 种可能，因而 P（抽到左手写 字学生）＝ ． 故选：C． 19．某班派 9 名同学参加拔河比赛，他们的体重分别是（单位：千克）：67、59、61、59、 63、57、70、59、65，这组数据的众数和中位数分别是（ ） A．59，63 B．59，61 C．59，59 D．57，61 【解答】解：从小到大排列此数据为：57、59、59、59、61、63、65、67、70，数据 59 第 28页（共 47页） 出现了三次最多为众数，61 处在第 5 位为中位数．所以本题这组数据的中位数是 61，众 数是 59． 故选：B． 20．众志成城，抗震救灾．某小组 7 名同学积极捐出自己的零花钱支援灾区，他们捐款的数 额分别是（单位/元）：50，20，50，30，50，25，135．这组数据的众数和中位数分别是 （ ） A．50，20 B．50，30 C．50，50 D．135，50 【解答】解：众数是一组数据中出现次数最多的数，在这一组数据中 50 是出现次数最多 的，故众数是 50；而将这组数据从小到大的顺序排列后，处于中间位置的那个数是 50， 那么由中位数的定义可知，这组数据的中位数是 50． 故选：C． 21．如图，有 5 张形状、大小、质地均相同的卡片，正面分别印有北京奥运会的会徽、吉祥 物（福娃）、火炬和奖牌等四种不同的图案，背面完全相同．现将这 5 张卡片洗匀后正面 向下放在桌子上，从中随机抽取一张，抽出的卡片正面图案恰好是吉祥物（福娃）的概 率是（ ） A． B． C． D． 【解答】解：五张卡片中有两张是吉祥物，故抽出吉祥物的概率是 ． 故选：B． 二．填空题（共 4 小题） 22．小天想要计算一组数据 92，90，94，86，99，85 的方差 s02，在计算平均数的过程中， 将这组数据中的每一个数都减去 90，得到一组新数据 2，0，4，﹣4，9，﹣5，记这组新 数据的方差为 s12，则 s12 ＝ s02（填“＞”，“＝”或”＜”） 【解答】解：∵一组数据中的每一个数据都加上（或都减去）同一个常数后，它的平均 数都加上（或都减去）这一个常数，两数进行相减，方差不变， ∴则 s12＝S02． 故答案为＝． 第 29页（共 47页） 23．从甲地到乙地有 A，B，C 三条不同的公交线路．为了解早高峰期间这三条线路上的公 交车从甲地到乙地的用时情况，在每条线路上随机选取了 500 个班次的公交车，收集了 这些班次的公交车用时（单位：分钟）的数据，统计如下： 公交车用时 公交车用时的频数 线路 30≤t≤35 35＜t≤40 40＜t≤45 45＜t≤50 合计 A 59 151 166 124 500 B 50 50 122 278 500 C 45 265 167 23 500 早高峰期间，乘坐 C （填“A”，“B”或“C”）线路上的公交车，从甲地到乙地“用 时不超过 45 分钟”的可能性最大． 【解答】解：∵A 线路公交车用时不超过 45 分钟的可能性为 ＝0.752， B 线路公交车用时不超过 45 分钟的可能性为 ＝0.444， C 线路公交车用时不超过 45 分钟的可能性为 ＝0.954， ∴C 线路上公交车用时不超过 45 分钟的可能性最大， 故答案为：C． 24．林业部门要考察某种幼树在一定条件下的移植成活率，下表是这种幼树在移植过程中的 一组数据： 移植的 棵数 n 1000 1500 2500 4000 8000 15000 20000 30000 成活的 棵数 m 865 1356 2220 3500 7056 13170 17580 26430 成活的 频率 0.865 0.904 0.888 0.875 0.882 0.878 0.879 0.881 估计该种幼树在此条件下移植成活的概率为 0.881 ． 【解答】解：概率是大量重复实验的情况下，频率的稳定值可以作为概率的估计值，即 次数越多的频率越接近于概率 第 30页（共 47页） ∴这种幼树移植成活率的概率约为 0.881． 故答案为：0.881． 25．北京市 2009﹣2014 年轨道交通日均客运量统计如图所示．根据统计图中提供的信息， 预估 2015 年北京市轨道交通日均客运量约 980 万人次，你的预估理由是 因为 2012 ﹣2013 年发生数据突变，故参照 2013﹣2014 增长进行估算． ． 【解答】解：参考答案 ① ：1038，按每年平均增长人数近似相等进行估算； 参考答案 ② ：980，因为 2012﹣2013 年发生数据突变，故参照 2013﹣2014 增长进行估 算．（因为题目问法比较灵活，只要理由合理均可给分，估计学生答出 980 至 1140 之间 均可给分） 三．解答题（共 12 小题） 26．国家创新指数是反映一个国家科学技术和创新竞争力的综合指数．对国家创新指数得分 排名前 40 的国家的有关数据进行收集、整理、描述和分析．下面给出了部分信息： a．国家创新指数得分的频数分布直方图（数据分成 7 组：30≤x＜40，40≤x＜50，50≤ x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）； b．国家创新指数得分在 60≤x＜70 这一组的是： 61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5 c．40 个国家的人均国内生产总值和国家创新指数得分情况统计图： 第 31页（共 47页） d．中国的国家创新指数得分为 69.5． （以上数据来源于《国家创新指数报告（2018）》） 根据以上信息，回答下列问题： （1）中国的国家创新指数得分排名世界第 17 ； （2）在 40 个国家的人均国内生产总值和国家创新指数得分情况统计图中，包括中国在 内的少数几个国家所对应的点位于虚线 l1 的上方，请在图中用“〇”圈出代表中国的点； （3）在国家创新指数得分比中国高的国家中，人均国内生产总值的最小值约为 2.8 万 美元；（结果保留一位小数） （4）下列推断合理的是 ①② ． ① 相比于点 A，B 所代表的国家，中国的国家创新指数得分还有一定差距，中国提出“加 快建设创新型国家”的战略任务，进一步提高国家综合创新能力； ② 相比于点 B，C 所代表的国家，中国的人均国内生产总值还有一定差距，中国提出“决 胜全面建成小康社会”的奋斗目标，进一步提高人均国内生产总值． 【解答】解：（1）∵国家创新指数得分为 69.5 以上（含 69.5）的国家有 17 个， ∴国家创新指数得分排名前 40 的国家中，中国的国家创新指数得分排名世界第 17， 故答案为：17； （2）如图所示： （3）由 40 个国家的人均国内生产总值和国家创新指数得分情况统计图可知，在国家创 新指数得分比中国高的国家中，人均国内生产总值的最小值约为 2.8 万美元； 故答案为：2.8； （4）由 40 个国家的人均国内生产总值和国家创新指数得分情况统计图可知， ① 相比于点 A、B 所代表的国家，中国的国家创新指数得分还有一定差距，中国提出“加 第 32页（共 47页） 快建设创新型国家”的战略任务，进一步提高国家综合创新能力；合理； ② 相比于点 B，C 所代表的国家，中国的人均国内生产总值还有一定差距，中国提出“决 胜全面建成小康社会”的奋斗目标，进一步提高人均国内生产总值；合理； 故答案为： ①② ． 27．某年级共有 300 名学生．为了解该年级学生 A，B 两门课程的学习情况，从中随机抽取 60 名学生进行测试，获得了他们的成绩（百分制），并对数据（成绩）进行整理、描述和 分析．下面给出了部分信息． a．A 课程成绩的频数分布直方图如下（数据分成 6 组：40≤x＜50，50≤x＜60，60≤x ＜70，70≤x＜80，80≤x＜90，90≤x≤100）： b．A 课程成绩在 70≤x＜80 这一组的是：70 71 71 71 76 76 77 78 78.5 78.5 79 79 79 79.5 c．A，B 两门课程成绩的平均数、中位数、众数如下： 课程 平均数 中位数 众数 A 75.8 m 84.5 B 72.2 70 83 根据以上信息，回答下列问题： 第 33页（共 47页） （1）写出表中 m 的值； （2）在此次测试中，某学生的 A 课程成绩为 76 分，B 课程成绩为 71 分，这名学生成绩 排名更靠前的课程是 B （填“A“或“B“），理由是 该学生的成绩小于 A 课程的中 位数，而大于 B 课程的中位数 ， （3）假设该年级学生都参加此次测试，估计 A 课程成绩超过 75.8 分的人数． 【解答】解：（1）∵A 课程总人数为 2+6+12+14+18+8＝60， ∴中位数为第 30、31 个数据的平均数，而第 30、31 个数据均在 70≤x＜80 这一组， ∴中位数在 70≤x＜80 这一组， ∵70≤x＜80 这一组的是：70 71 71 71 76 76 77 78 78.5 78.5 79 79 79 79.5， ∴A 课程的中位数为 ＝78.75，即 m＝78.75； （2）∵该学生的成绩小于 A 课程的中位数，而大于 B 课程的中位数， ∴这名学生成绩排名更靠前的课程是 B， 故答案为：B、该学生的成绩小于 A 课程的中位数，而大于 B 课程的中位数． （3）估计 A 课程成绩超过 75.8 分的人数为 300× ＝180 人． 28．某工厂甲、乙两个部门各有员工 400 人，为了解这两个部门员工的生产技能情况，进行 了抽样调查，过程如下，请补充完整． 收集数据 从甲、乙两个部门各随机抽取 20 名员工，进行了生产技能测试，测试成绩（百分制）如 下： 甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77 乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40 整理、描述数据 按如下分数段整理、描述这两组样本数据： 第 34页（共 47页） 成绩 x 人数 部门 40≤x≤49 50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤ 100 甲 0 0 1 11 7 1 乙 1 0 0 7 10 2 （说明：成绩 80 分及以上为生产技能优秀，70﹣﹣79 分为生产技能良好，60﹣﹣69 分 为生产技能合格，60 分以下为生产技能不合格） 分析数据 两组样本数据的平均数、中位数、众数如下表所示： 部门 平均数 中位数 众数 甲 78.3 77.5 75 乙 78 80.5 81 得出结论：a．估计乙部门生产技能优秀的员工人数为 240 ；b．可以推断出 甲或乙 部门员工的生产技能水平较高，理由为 ① 甲部门生产技能测试中，平均分较高，表示 甲部门员工的生产技能水平较高； ② 甲部门生产技能测试中，没有技能不合格的员工，表示甲部门员工的生产技能水平较 高． 或 ① 乙部门生产技能测试中，中位数较高，表示乙部门员工的生产技能水平较高； ② 乙部门生产技能测试中，众数较高，表示乙部门员工的生产技能水平较高． ．（至少 从两个不同的角度说明推断的合理性） 【解答】解：填表如下： 成绩 x 人数 部门 40≤x≤49 50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤ 100 甲 0 0 1 11 7 1 乙 1 0 0 7 10 2 a. ×400＝240（人）． 故估计乙部门生产技能优秀的员工人数为 240； 第 35页（共 47页） b．答案不唯一，理由合理即可． 可以推断出甲部门员工的生产技能水平较高，理由为： ① 甲部门生产技能测试中，平均分较高，表示甲部门员工的生产技能水平较高； ② 甲部门生产技能测试中，没有技能不合格的员工，表示甲部门员工的生产技能水平较 高． 或可以推断出乙部门员工的生产技能水平较高，理由为： ① 乙部门生产技能测试中，中位数较高，表示乙部门员工的生产技能水平较高； ② 乙部门生产技能测试中，众数较高，表示乙部门员工的生产技能水平较高． 故答案为：1，0，0，7，10，2； 240；甲或乙， ① 甲部门生产技能测试中，平均分较高，表示甲部门员工的生产技能水平 较高； ② 甲部门生产技能测试中，没有技能不合格的员工，表示甲部门员工的生产技能水平较 高； 或 ① 乙部门生产技能测试中，中位数较高，表示乙部门员工的生产技能水平较高； ② 乙部门生产技能测试中，众数较高，表示乙部门员工的生产技能水平较高． 29．调查作业：了解你所在小区家庭 5 月份用气量情况： 小天、小东和小芸三位同学住在同一小区，该小区共有 300 户家庭，每户家庭人数在 2 ﹣5 之间，这 300 户家庭的平均人数约为 3.4． 小天、小东和小芸各自对该小区家庭 5 月份用气量情况进行了抽样调查，将收集的数据 进行了整理，绘制的统计表分别为表 1，表 2 和表 3． 表 1 抽样调查小区 4 户家庭 5 月份用气量统计表 （单位：m3） 家庭人数 2 3 4 5 用气量 14 19 21 26 表 2 抽样调查小区 15 户家庭 5 月份用气量统计表 （单位：m3） 家庭 人数 2 2 2 3 3 3 3 3 3 3 3 3 3 3 4 用气 量 10 11 15 13 14 15 15 17 17 18 18 18 18 20 22 表 3 抽样调查小区 15 户家庭 5 月份用气量统计表 （单位：m3） 第 36页（共 47页） 家庭 人数 2 2 3 3 3 3 3 3 3 4 4 4 4 5 5 用气 量 10 12 13 14 17 17 18 19 20 20 22 26 31 28 31 根据以上材料回答问题： 小天、小东和小芸三人中，哪一位同学抽样调查的数据能较好地反映该小区家庭 5 月份 用气量情况，并简要说明其他两位同学抽样调查的不足之处． 【解答】解：小天调查的人数太少，小东抽样的调查数据中，家庭人数的平均值为： （2×3+3×11+4）÷15≈2.87， 远远偏离了平均人数的 3.4，所以他的数据抽样有明显的问题， 小芸抽样的调查数据中，家庭人数的平均值为：（2×2+3×7+4×4+5×2）÷15＝3.4， 说明小芸抽样数据质量较好，因此小芸的抽样调查的数据能较好的反应出该小区家庭 5 月份用气量情况． 30．阅读下列材料： 2015 年清明小长假，北京市属公园开展以“清明踏青，春色满园”为主题的游园活动， 虽然气温小幅走低，但游客踏青赏花的热情很高，市属公园游客接待量约为190万人次．其 中，玉渊潭公园的樱花、北京植物园的桃花受到了游客的热捧，两公园的游客接待量分 别为 38 万人次、21.75 万人次；颐和园、天坛公园、北海公园因皇家园林的厚重文化底 蕴与满园春色成为游客的重要目的地，游客接待量分别为 26 万人次、20 万人次、17.6 万人次；北京动物园游客接待量为 18 万人次，熊猫馆的游客密集度较高． 2014 年清明小长假，天气晴好，北京市属公园游客接待量约为 200 万人次，其中，玉渊 潭公园游客接待量比 2013 年清明小长假增长了 25%；颐和园游客接待量为 26.2 万人次， 比 2013 年清明小长假增加了 4.6 万人次；北京动物园游客接待量为 22 万人次． 2013 年清明小长假，玉渊潭公园、陶然亭公园、北京动物园游客接待量分别为 32 万人次、 13 万人次、14.9 万人次． 根据以上材料解答下列问题： （1）2014 年清明小长假，玉渊潭公园游客接待量为 40 万人次； （2）选择统计表或统计图，将 2013﹣2015 年清明小长假玉渊潭公园、颐和园和北京动 物园的游客接待量表示出来． 第 37页（共 47页） 【解答】解：（1）2014 年，玉渊潭公园的游客接待量是：32×（1+25%）＝40（万人）． 故答案是：40； （2）2013 年颐和园的游客接待量是：26.2﹣4.6＝21.6（万元）． 玉渊潭公园 颐和园 北京动物园 2013 年 32 21.6 14.9 2014 年 40 26.2 22 2015 年 38 26 18 31．根据某研究院公布的 2009～2013 年我国成年国民阅读调查报告的部分相关数据，绘制 的统计图表如下： 2009～2013 年成年国民 年人均阅读图书数量统计表 年份 年人均阅读图书数 量（本） 2009 3.88 2010 4.12 2011 4.35 2012 4.56 2013 4.78 根据以上信息解答下列问题： （1）直接写出扇形统计图中 m 的值； （2）从 2009 到 2013 年，成年国民年人均阅读图书的数量每年增长的幅度近似相等，估 算 2014 年成年国民年人均阅读图书的数量约为 5 本； （3）2013 年某小区倾向图书阅读的成年国民有 990 人，若该小区 2014 年与 2013 年成年 国民的人数基本持平，估算 2014 年该小区成年国民阅读图书的总数量约为 4950 本． 第 38页（共 47页） 【解答】解：（1）m%＝1﹣1.0%﹣15.6%﹣2.4%﹣15.0%＝66%， ∴m＝66． （2）∵年平均增长幅度为（4.78﹣3.88）÷4＝0.225（本）， ∴2014 年的阅读量为：4.78+0.225≈5（本）； 故答案为：5； （3）2014 年该小区成年国民阅读图书的总数量约为：990×5＝4950（本）． 故答案为：4950． 32．第九届中国国际园林博览会（园博会）已于 2013 年 5 月 18 日在北京开幕，以下是根据 近几届园博会的相关数据绘制的统计图的一部分． （1）第九届园博会的植物花园区由五个花园组成，其中月季园面积为 0.04 平方千米，牡 丹园面积为 0.03 平方千米； （2）第九届园博会会园区陆地面积是植物花园区总面积的 18 倍，水面面积是第七、八 第 39页（共 47页） 界园博会的水面面积之和，请根据上述信息补全条形统计图，并标明相应数据； （3）小娜收集了几届园博会的相关信息（如下表），发现园博会园区周边设置的停车位 数量与日均接待游客量和单日最多接待游客量中的某个量近似成正比例关系．根据小娜 的发现，请估计，将于 2015 年举办的第十届园博会大约需要设置的停车位数量（直接写 出结果，精确到百位）． 第七届至第十届园博会游客量和停车位数量统计表： 日接待游客量 （万人次） 单日最多接待游客量 （万人次） 停车位数量 （个） 第七届 0.8 6 约 3000 第八届 2.3 8.2 约 4000 第九届 8（预计） 20（预计） 约 10500 第十届 1.9（预计） 7.4（预计） 约 3.7×103 【解答】解：（1）∵月季园面积为 0.04 平方千米，月季园所占比例为 20%， 则牡丹园的面积为：15%× ＝0.03（平方千米）； 故答案为 0.03； （2）植物花园的总面积为：0.04÷20%＝0.2（平方千米）， 则第九届园博会会园区陆地面积为：0.2×18＝3.6（平方千米）， 第七、八界园博会的水面面积之和为：1+0.5＝1.5（平方千米）， 则第九届园博会水面面积为 1.5 平方千米， 如图： 第 40页（共 47页） （3）由图标可得，停车位数量与单日最多接待游客量成正比例关系，比值约为 500， 则第十届园博会大约需要设置的停车位数量约为：500×7.4≈3.7×103．． 故答案为：3.7×103． 33．近年来，北京市大力发展轨道交通，轨道运营里程大幅增加，2011 年北京市又调整修 订了 2010 至 2020 年轨道交通线网的发展规划．以下是根据北京市轨道交通指挥中心发 布的有关数据制作的统计图表的一部分． 北京市轨道交通已开通线路相关数据统计表（截止 2010 年底） 开通时间 开通线路 运营里程（千米） 1971 1 号线 31 1984 2 号线 23 2003 13 号线 41 八通线 19 2007 5 号线 28 2008 8 号线 5 10 号线 25 机场线 28 2009 4 号线 28 房山线 22 第 41页（共 47页） 2010 大兴线 22 亦庄线 23 昌平线 21 15 号线 20 请根据以上信息解答下列问题： （1）补全条形统计图并在图中标明相应数据； （2）按照 2011 年规划方案，预计 2020 年北京市轨道交通运营总里程将达到多少千米？ （3）要按时完成截至 2015 年的轨道交通规划任务，从 2011 到 2015 年这 4 年中，平均 每年需新增运营里程多少千米？ 【解答】解：（1）根据表格所给数据即可得出：2009 年运营路程为：200+28＝228， 如图所示： 第 42页（共 47页） （2）根据扇形图得出：截止 2010 年已开通运营总路程占计划的百分比，进而得出 预计 2020 年北京市轨道交通运营总里程将达到：336÷33.6%＝1000（千米）， 答：预计 2020 年北京市轨道交通运营总里程将达到 1000 千米； （3）根据截止 2015 年新增运营路程为：1000×36.7%＝367（千米）； 则从 2011 到 2015 年这 4 年中，平均每年需新增运营里程[367﹣（372﹣336）]÷4＝82.75． 答：从 2011 到 2015 年这 4 年中，平均每年需新增运营里程 82.75 千米． 34．以下是根据北京市国民经济和社会发展统计公报中的相关数据，绘制统计图的一部分． 请根据以上信息解答下列问题： （1）2008 年北京市私人轿车拥有是多少万辆（结果保留三个有效数字）？ （2）补全条形统计图； （3）汽车数量增多除造成交通拥堵外，还增加了碳排放量，为了了解汽车碳排放量的情 况，小明同学通过网络了解到汽车的碳排放量与汽车排量有关．如：一辆排量为 1.6L 的 轿车，如果一年行驶 1 万千米，这一年，它碳排放量约为 2.7 吨．于是他调查了他所居住 小区的 150 辆私人轿车，不同排量的轿车数量如下表所示． 排量（L） 小于 1.6 1.6 1.8 大于 1.8 数量（辆） 29 75 31 15 如果按照小明的统计数据，请你通过计算估计，2010 年北京市仅排量为 1.6L 的这类私人 第 43页（共 47页） 轿车（假设每辆车平均一行行驶 1 万千米）的碳排放总量约为多少万吨？ 【解答】解：（1）146×（1+19%）， ＝173.74， ≈174（万辆）， 所以 2008 年北京市私人轿车拥有量约是 174 万辆； （2）如图． （3）276× ×2.7＝372.6（万吨）， 所以估计 2010 年北京市仅排量为 1.6L 的这类私人轿车的碳排放总量约为 372.6 万吨． 35．根据北京市统计局的 2006﹣2009 年空气质量的相关数据，绘制统计图如下： （1）由统计图中的信息可知，北京全年市区空气质量达到二级和好于二级的天数与上一 年相比，增加最多的是 2008 年，增加了 28 天； （2）表 1 是根据《中国环境发展报告（2010）》公布的数据绘制的 2009 年十个城市供气 质量达到二级和好于二级的天数占全年天数百分比的统计表，请将表 1 中的空缺部分补 充完整（精确到 1%）． 2009 年十个城市空气质量达到二级和好于二级的天数占全年天数百分比统计表：3 第 44页（共 47页） 城市 北京 上海 天津 昆明 杭州 广州 南京 成都 沈阳 西宁 百分比 91% 84% 100% 89% 95% 86% 86% 90% 77% （3）根据表 1 中的数据将十个城市划分为三个组，百分比不低于 95%的为 A 组，不低于 85%且低于 95%的为 B 组，低于 85%的为 C 组．按此标准，C 组城市数量在这十个城市 中所占的百分比为 30 %；请你补全右边的扇形统计图． 【解答】解： （1）根据折线统计图，得 增加最多的一年是 2008 年；274﹣246＝28（天）； （2）285÷365≈78%； （3）3÷10＝30%． 36．在每年年初召开的市人代会上，北京市财政局都要报告上一年度市财政预算执行情况和 当年预算情况．以下是根据 2004﹣2008 年度报告中的有关数据制作的市财政教育预算与 实际投入统计图表的一部分． 2004﹣2008 年北京市财政教育实际投入与预算差值统计表（单位：亿元） 年份 2004 2005 2006 2007 2008 教育实际投 入与预算差值 6.7 5.7 14.6 7.3 第 45页（共 47页） 请根据以上信息解答下列问题： （1）请在表 1 的空格内填入 2004 年市财政教育实际投入与预算的差值； （2）求 2004﹣2008 年北京市财政教育实际投入与预算差值的平均数； （3）已知 2009 年北京市财政教育预算是 141.7 亿元．在此基础上，如果 2009 年北京市 财政教育实际投入按照（2）中求出的平均数增长，估计它的金额可能达到多少亿元？ 【解答】解： （1）2004 年市财政教育实际投入与预算的差值＝52.2﹣44.2＝8 亿元． 年份 2004 2005 2006 2007 2008 教育实际投 入与预算差值 8 6.7 5.7 14.6 7.3 ； （2） （亿元）， 所以 2004﹣2008 年市财政教育实际投入与预算差值的平均数是 8.46 亿元； （3）141.7+8.46＝150.16（亿元）， 估计 2009 年市财政教育实际投入可能达到 150.16 亿元． 37．为减少环境污染，自 2008 年 6 月 1 日起，全国的商品零售场所开始实行“塑料购物袋 有偿使用制度”（以下简称“限塑令”）．某班同学于 6 月上旬的一天，在某超市门口采用 问卷调查的方式，随机调查了“限塑令”实施前后，顾客在该超市用购物袋的情况，以 下是根据 100 位顾客的 100 份有效答卷画出的统计图表的一部分： 第 46页（共 47页） “限塑令”实施后，塑料购物袋使用后的处理方式统计表： 处理方式 直接丢弃 直接做垃圾袋 再次购物使用 其它 选该项的人数占 总人数的百分比 5% 35% 49% 11% 请你根据以上信息解答下列问题： （1）补全图 1，“限塑令”实施前，如果每天约有 2 000 人次到该超市购物．根据这 100 位顾客平均一次购物使用塑料购物袋的平均数，估计这个超市每天需要为顾客提供多少 个塑料购物袋？ （2）补全图 2，并根据统计图和统计表说明，购物时怎样选用购物袋，塑料购物袋使用 后怎样处理，能对环境保护带来积极的影响． 【解答】解： （1）补全图 1 见下图． 因为 （个），即这 100 位顾客 平均一次购物使用塑料购物袋的平均数为 3 个．因为 2000×3＝6000，所以估计这个超市 第 47页（共 47页） 每天需要为顾客提供 6000 个塑料购物袋． （2）图 2 中，使用收费塑料购物袋的人数所占百分比为 25%． 例如：由图 2 和统计表可知，购物时应尽量使用自备袋和押金式环保袋，少用塑料购物 袋；塑料购物袋应尽量循环使用，以便减少塑料购物袋的使用量，为环保做贡献． 声明：试 题解析著作权 属菁优网所有 ，未经书面同 意，不得复制 发布 日期：2020/2/3 0:15:23 ；用户： 金雨教育；邮 箱：309593466@qq.com ；学号：335385