中考数学一轮复习知识点+题型专题讲义12 一元二次方程（学生版） 10页

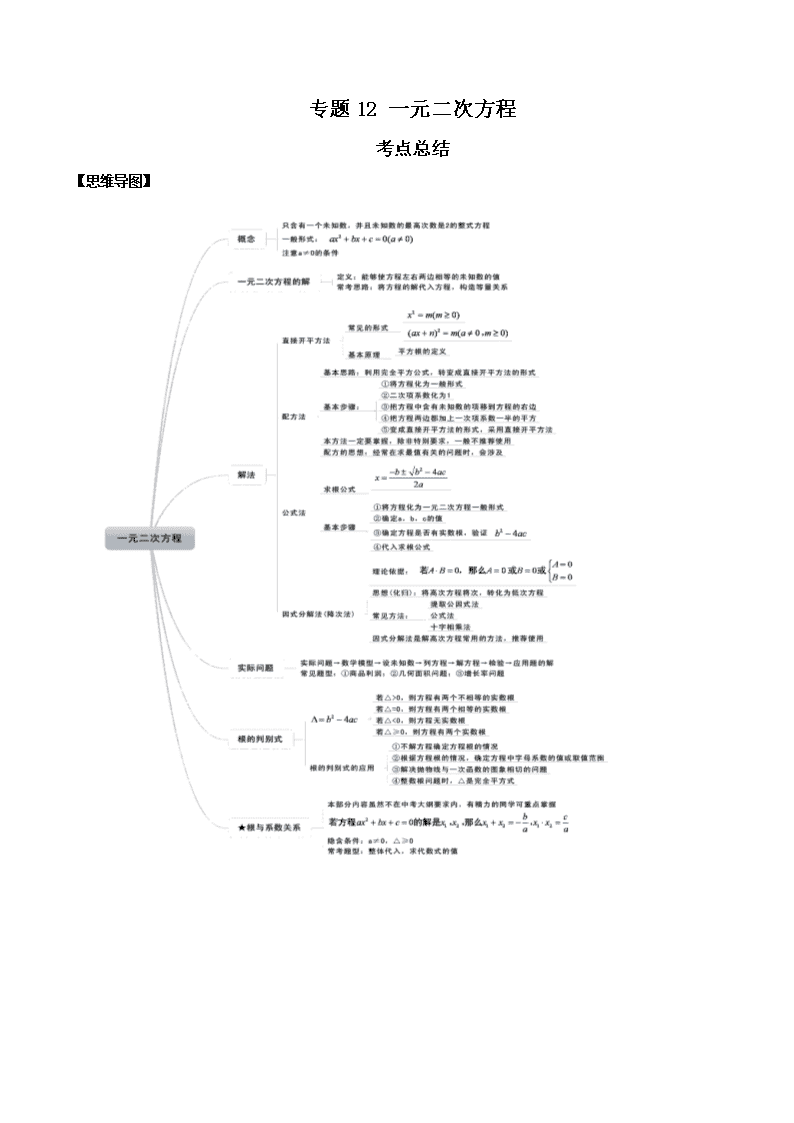
专题 12 一元二次方程 考点总结 【思维导图】 【知识要点】 知识点一 一元二次方程定义及一般形式 概念：等号两边都是整式，只含有一个未知数（一元），并且未知数的最高次数式 2（二次）的方程，叫做 一元二次方程。 一般形式： 2 0( 0)ax bx c a    。其中 a 为二次项系数，b 为一次项系数，c 为常数项。 【注意】 1）只含有一个未知数； 2）所含未知数的最高次数是 2； 3）整式方程。 1．（2019·四川中考模拟）下列方程，是一元二次方程的是（ ） ①3x2+x=20，②2x2-3xy+4=0，③x2- 1 x =4，④x2=0，⑤x2- 3 x +3=0 A．①② B．①④⑤ C．①③④ D．①②④⑤ 2．（2019·广西柳州二十五中中考模拟）根据下列表格的对应值，判断方程 ax2+bx+c=0（a≠0，a、b、c为常 数）一个解的范围是（ ） x 3.23 3.24 3.25 3.26 ax2+bx+c ﹣0.06 ﹣0.02 0.03 0.09 A．3＜x＜3.23 B．3.23＜x＜3.24 C．3.24＜x＜3.25 D．3.25＜x＜3.26 3．（2019·广东中考模拟）方程 2x2﹣3x﹣5=0的二次项系数、一次项系数、常数项分别为（ ） A．3、2、5 B．2、3、5 C．2、﹣3、﹣5 D．﹣2、3、5 4．（2018·湖南中考模拟）下列方程中是关于 x的一元二次方程的是（ ） A． 2 2 1 0x x   B． 2 0ax bx c   C．   1 2 1x x   D． 2 23 2 5 0x xy y   5．（2018·湖北中考模拟）下列关于 x的方程中，属于一元二次方程的是（ ） A．x﹣1=0 B．x2+3x﹣5=0 C．x3+x=3 D．ax2+bx+c=0 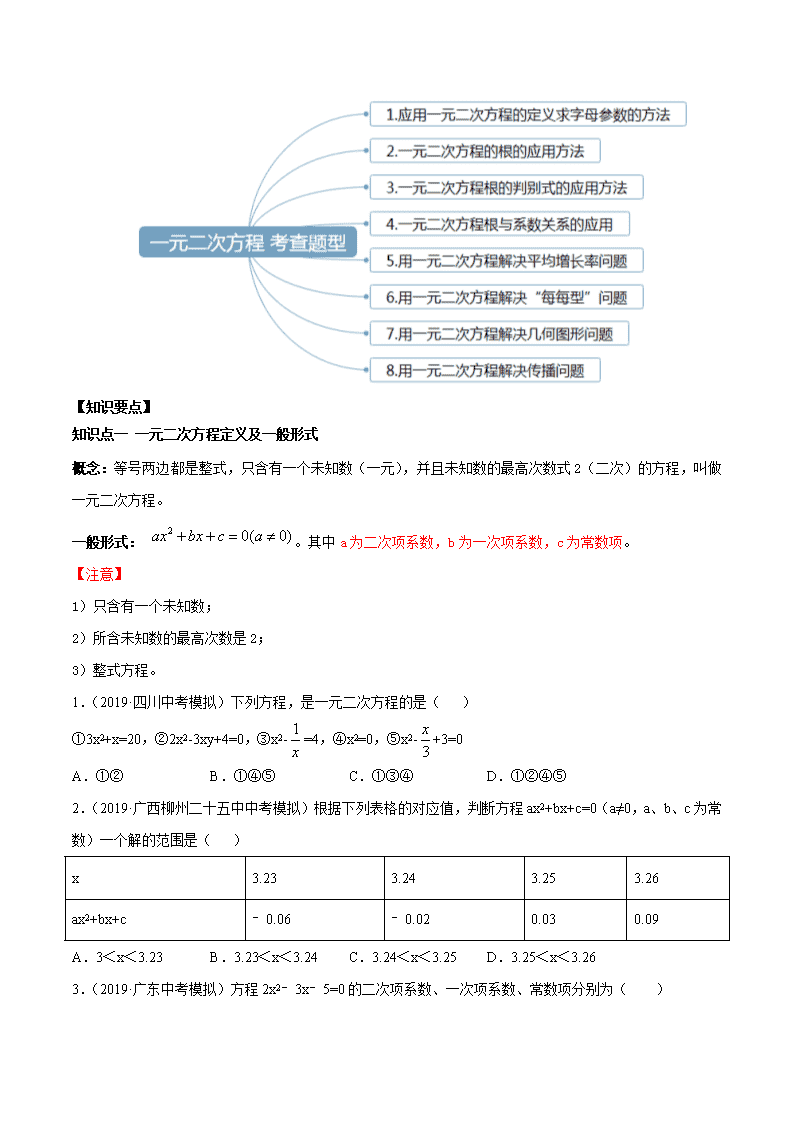考查题型一 应用一元二次方程的定义求字母参数的方法 1．（2019·吉林中考模拟）若关于 x的方程   2m 1 1 0x mx    是一元二次方程，则 m的取值范围是（ ） A．m 1 . B．m 1 . C．m 1 D．  m 0 . 2．（2019·四川中考模拟）若   2 22 3aa x   是关于 x的一元二次方程，则 a 的值是（ ） A．0 B．2 C．-2 D．±2 3．（2017·重庆中考模拟）若方程    2 11 1 2 0mm x m x     是一元二次方程，则 m的值为（ ） A．0 B．±1 C．1 D．–1 4．（2019·汕头市潮南区阳光实验学校中考模拟）关于 x 的一元二次方程（m﹣1）x2+5x+m2﹣3m+2＝0的常 数项为 0，则 m 等于（ ） A．1 B．2 C．1或 2 D．0 考查题型二 一元二次方程的根的应用方法 1．（2019·四川中考模拟）若 n（ 0n  ）是关于 x的方程 2 2 0x mx n   的根，则 m+n的值为（ ） A．1 B．2 C．-1 D．-2 2．（2019·中山市杨仙逸中学中考模拟）已知 y＝0是关于 y的一元二次方程（m﹣1）y2+my+4m2﹣4＝0的 一个根，那么 m的值是（ ） A．0 B．±1 C．1 D．﹣1 3．（2018·河北中考模拟）若关于 x的一元二次方程 ax2+bx+6=0的一个根为 x=﹣2，则代数式 6a﹣3b+6的 值为（ ） A．9 B．3 C．0 D．﹣3 知识点 2：解一元二次方程（重点） 方法一：配方法（最基础的解法） 配方的过程需注意：若方程二次项系数为 1 时，“方程两边加一次项系数一半的平方” 用配方法解一元二次方程 2 0( 0)ax bx c a    的一般步骤  移项：使方程左边为二次项与一次项，右边为常数项；  二次项系数化为 1：方程两边都除以二次项系数；  配方：方程两边都加上一次项系数一般的平方，把方程化为 2( ) ( 0)x m n n   的形式； 【注意】：1）当 0n  时，方程无解 2）若方程二次项系数为 1 时，“方程两边加一次项系数一半的平方”  求解：判断右边等式符号，开平方并求解。 1．（2019·江苏中考真题）用配方法解方程 2 8 9 0x x   ，变形后的结果正确的是( ) A．  24 9x    B．  24 7x    C．  24 25x   D．  24 7x   2.．（2018·浙江中考模拟）用配方法解一元二次方程 x2﹣6x﹣1=0时，下列变形正确的是（ ） A．（x﹣3）2=1 B．（x﹣3）2=10 C．（x+3）2=1 D．（x+3）2=10 3.．（2015·湖北中考真题）用配方法解一元二次方程 x2﹣6x﹣4=0，下列变形正确的是（ ） A．（x﹣6）2=﹣4+36 B．（x﹣6）2=4+36 C．（x﹣3）2=﹣4+9 D．（x﹣3）2=4+9 方法二：直接开平方法（最基础的解法） 概念：形如 2( ) ( 0)x a b b   的方程可以用直接开平方法解，两边直接开平方得 x a b  或者 x a b   ，最后通过解两个一元一次方程得到原方程的解。 【注意】 1)若 b≥0，方程有两个实数根。 （若 b>0，方程有两个不相等的实数根；若 b=0，方程有两个相等的实数根） 2)若 b<0，方程无解。 1．（2019·江苏中考模拟）一元二次方程 ( 1)( 3) 2 5x x x    根的情况是（ ） A．无实数根 B．有一个正根，一个负根 C．有两个正根，且都小于 3 D．有两个正根，且有一根大于 3 2．（2019·四川中考模拟）对于两个实数 a ，b ，用  max ,a b 表示其中较大的数，则方程  max , 2 1x x x x    的解是（ ） A．1，1 2 B．1，1 2 C． 1 ，1 2 D． 1 ，1 2 3．（2018·福建中考模拟）设一元二次方程（ 1x  ）（ 3x  ）=m（m＞0）的两实数根分别为α、β且α＜β， 则α、β满足（ ） A．-1＜α＜β＜3 B．α＜-1且β＞3 C．α＜-1＜β＜3 D．-1＜α＜3＜β 方法三：公式法（常用解法） 一元二次方程 2 0( 0)ax bx c a    根的判别式： 2 4b ac    0  方程有两个不相等的实根: 2 4 2 b b acx a     （ 2 4 0b ac  ） ( )f x 的图像与 x轴有两 个交点  0  方程有两个相等的实根 ( )f x 的图像与 x轴有一个交点  0  方程无实根 ( )f x 的图像与 x轴没有交点 用公式法解一元二次方程 2 0( 0)ax bx c a    的一般步骤：  把方程化为一般形式，确定 a、b、c 的值(若系数是分数通常将其化为整数，方便计算);  求出 b 2 -4ac 的值，根据其值的情况确定一元二次方程是否有解;  如果 b 2 -4ac≥0, 将 a、b、c 的值代入求根公式： 2 4 2 b b acx a      最后求出 x1，x2 1．（2019·广西中考模拟）关于 x的方程 2( 5) 4 1 0a x x    有实数根，则 a 满足（ ） A． 1a  B． 1a  且 5a  C． 1a  且 5a  D． 5a  2．（2019·福建中考模拟）不解方程，判别方程 2x2﹣3 2 x＝3的根的情况( ) A．有两个相等的实数根 B．有两个不相等的实数根 C．有一个实数根 D．无实数根 3．（2019·新疆中考模拟）已知关于 x 的一元二次方程 22 3 0x kx   有两个相等的实根，则 k 的值为（ ） A． 2 6 B． 6 C．2或 3 D． 2 或 3 考查题型三 一元二次方程根的判别式的应用方法 1．（2019·河南中考模拟）关于 x 的一元二次方程（k﹣1）x2﹣2x+3＝0有两个实数根，则 k 的取值范围是（ ） A．k≤ 4 3 且 k≠1 B．k≤ 4 3 C．k＜ 4 3 且 k≠1 D．k＜ 4 3 2．（2015·四川中考真题）方程݉ െെ ݉ = 有两个实数根，则 ݉的取值范围（ ） A．݉ > െ B．݉ െ 且 ݉ െ C．݉ ≥ D．݉ 且 ݉ െ 3．（2019·安徽中考模拟）若关于 x的一元二次方程 2 22( 1) 1 0x k x k     有实数根，则 k的取值范围是 （ ） A．k≥1 B．k＞1 C．k＜1 D．k≤1 4．（2018·广东中考模拟）关于 x 的一元二次方程 x2-2x-（m-1）=0有两个不相等的实数根，则实数 m 的取 值范围是（ ） A． 0m  且 1m  B． 0m  C． 0m  且 1m  D． 0m  5．（2019·湖北中考模拟）关于 x的一元二次方程 2 3 0x x m   有两个不相等的实数根，则实数m 的取值 范围是 ( ) A． 9 4 m  B． 9 4 m„ C． 9 4 m  D． 9 4 m… 方法四：因式分解法（仔细观察方程，灵活使用） 用因式分解一元二次方程 2 0( 0)ax bx c a    的一般步骤：  将方程右边得各项移到方程左边，使方程右边为 0；  将方程左边分解为两个一次因式相乘的形式；  令每个因式分别为零，得到两个一元一次方程；  求解 归纳：右化零，左分解，两因式，各求解 1．（2019·湖州市南浔区南浔锦绣实验学校中考模拟）若 x＝－2是关于 x 的一元二次方程 x2＋ 3 2 ax－a2＝0 的一个根，则 a 的值为（ ） A．－1或 4 B．－1或－4 C．1或－4 D．1或 4 2．（2019·长沙市南雅中学中考模拟）三角形两边长分别为 4和 6，第三边是方程 x2﹣13x+36＝0的根，则三 角形的周长为（ ） A．14 B．18 C．19 D．14或 19 3．（2013·宁夏中考真题）一元二次方程  x x 2 2 x   的根是 A．﹣1 B．2 C．1和 2 D．﹣1和 2 4．（2018·四川中考模拟）已知一元二次方程 x2-8x+15=0的两个解恰好分别是等腰△ABC 的底边长和腰长， 则△ABC的周长为（ ） A．13 B．11或 13 C．11 D．12 方法五：韦达定理（根与系数关系） 我们将一元二次方程化成一般式 ax 2 +bx+c＝0（a ，Δ ≥ ）之后，设它的两个根是 1x 和 2x ，则 1x 和 2x 与 方程的系数 a，b，c 之间有如下关系： 1x + 2x ＝ b a  ； 1x  2x ＝ c a 考查题型四 一元二次方程根与系数关系的应用 1．（2017·湖北中考模拟）已知 mn≠1，且 5m2+2010m+9=0，9n2+2010n+5=0，则 m n 的值为（ ） A．﹣402 B． 5 9 C． 9 5 D． 670 3 2．（2019·贵州中考真题）一元二次方程 x2﹣3x+1＝0的两个根为 x1，x2，则 x12+3x2+x1x2﹣2的值是（ ） A．10 B．9 C．8 D．7 3．（2017·广东中考模拟）关于的方程 2 2 0x ax a   的两根的平方和是 5，则 a 的值是( ) A．-1或 5 B．1 C．5 D．-1 4.（2019·湖北中考真题）关于 x 的一元二次方程 2 4 0x x m   的两实数根分别为 1x 、 2x ，且 1 23 5x x  ， 则 m 的值为（ ） A． 7 4 B． 7 5 C． 7 6 D．0 5．（2019·广州市第六十五中学中考模拟）已知 a、b 为一元二次方程 2 2 9 0x x   的两个根，那么 2a a b  的值为（ ） A．-7 B．0 C．7 D．11 知识点 4： 一元二次方程的应用 列一元二次方程解应用题，其步骤和二元一次方程组解应用题类似：  “审”，弄清楚已知量，未知量以及他们之间的等量关系；  “设”指设元，即设未知数，可分为直接设元和间接设元；  “列”指列方程，找出题目中的等量关系，再根据这个关系列出含有未知数的等式，即方程。  “解”就是求出说列方程的解；  “答”就是书写答案，检验得出的方程解，舍去不符合实际意义的方程。 注意：一元二次方程考点：定义的考察；解方程及一元二次方程的应用。 考查题型五 用一元二次方程解决平均增长率问题 1．（2018·河南中考模拟）某种品牌运动服经过两次降价，每件零售价由 560元降为 315元，已知两次降价 的百分率相同，求每次降价的百分率．设每次降价的百分率为 x，下面所列的方程中正确的是（ ） A．560（1＋x）2＝315 B．560（1－x）2＝315 C．560（1－2x）2＝315 D．560（1－x2）＝315 2．（2013·甘肃中考真题）某超市一月份的营业额为 36万元，三月份的营业额为 48万元，设每月的平均增 长率为 x，则可列方程为（ ） A．48（1﹣x）2=36 B．48（1+x）2=36 C．36（1﹣x）2=48 D．36（1+x）2=48 3．（2018·安徽中考模拟）某企业因春节放假，二月份产值比一月份下降 20%，春节后生产呈现良好上升势 头，四月份比一月份增长15%，设三、四月份的月平均增长率为 x，则下列方程正确的是 ( ) A．   2 1 20% 1 1 15%x    B．   21 15% (1 ) 1 20%x    C．   2 1 15% 1 1 20%x    D．   21 20% (1 ) 1 15%x    考查题型六 用一元二次方程解决“每每型”问题 1．（2018·海南中考模拟）某商场销售一批名牌衬衫，平均每天可售出 20件，每件盈利 40元，为扩大销售， 尽快减少库存，商场决定釆取降价措施，调查发现，每件衬衫，每降价 1元，平均每天可多销售 2件，若 商场每天要盈利 1200元，每件衬衫应降价（ ） A．5元 B．10元 C．20元 D．10元或 20元 2．（2019·忻城县民族中学中考模拟）宾馆有 50间房供游客居住，当每间房每天定价为 180元时，宾馆会住 满；当每间房每天的定价每增加 10元时，就会空闲一间房.如果有游客居住，宾馆需对居住的每间房每天支 出 20元的费用.当房价定为 x元时，宾馆当天的利润为 10890元.则有( ) A． (180 20) 50 10890 10 xx         B． 18050 50 20 10890 10 xx         C． 180( 20) 50 10890 10 xx        D． ( 180) 50 50 20 10890 10 xx          3.（2019·山东中考模拟）一商店销售某种商品，平均每天可售出 20件，每件盈利 40元.为了扩大销售、增 加盈利，该店采取了降价措施，在每件盈利不少于 25元的前提下，经过一段时间销售，发现销售单价每降 低 1元，平均每天可多售出 2件. （1）若降价 3元，则平均每天销售数量为________件； （2）当每件商品降价多少元时，该商店每天销售利润为 1200元？ 考查题型七 用一元二次方程解决几何图形问题 1．（2019·广西中考模拟）如图，有一张矩形纸片，长 10cm，宽 6cm，在它的四角各减去一个同样的小正方 形，然后折叠成一个无盖的长方体纸盒．若纸盒的底面（图中阴影部分）面积是 32cm2，求剪去的小正方形 的边长．设剪去的小正方形边长是 xcm，根据题意可列方程为（ ） A．10×6﹣4×6x=32 B．（10﹣2x）（6﹣2x）=32 C．（10﹣x）（6﹣x）=32 D．10×6﹣4x2=32 2（2019·广西中考真题）扬帆中学有一块长30m，宽 20m的矩形空地，计划在这块空地上划出四分之一的 区域种花，小禹同学设计方案如图所示，求花带的宽度．设花带的宽度为 xm，则可列方程为（ ） A．     330 20 20 30 4 x x     B．     130 2 20 20 30 4 x x     C． 130 2 20 20 30 4 x x     D．     330 2 20 20 30 4 x x     3．（2012·广东中考模拟）在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂 图，如图所示，如果要使整幅挂图的面积是 25400cm ，设金色纸边的宽为 xcm ，那么 x满足的方程是（ ） A． 2 130 1400 0x x   B． 2 65 350 0x x   C． 2 130 1400 0x x   D． 2 65 350 0x x   4．（2019·安徽中考模拟）如图，某小区计划在一块长为 32m，宽为 20m 的矩形空地上修建三条同样宽的道 路，剩余的空地上种植草坪．若草坪的面积为 570m2，道路的宽为 xm，则可列方程为（ ） A．32×20﹣2x2＝570 B．32×20﹣3x2＝570 C．（32﹣x）（20﹣2x）＝570 D．（32﹣2x）（20﹣x）＝570 考查题型八 用一元二次方程解决传播问题 1．（2019·黑龙江中考真题）某校“研学”活动小组在一次野外实践时，发现一种植物的主干长出若干数目的 支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是 43，则这种植物每个支干长出的 小分支个数是（ ） A．4 B．5 C．6 D． 7 2．（2018·安徽中考模拟）某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念，全班共送 1035 张照片，如果全班有 x名同学，根据题意，列出方程为（ ） A．x(x+1)=1035 B．x(x-1)=1035 C． 1 2 x(x+1)=1035 D． 1 2 x(x-1)=1035 3．（2019·天津中考模拟）某校羽毛球队有若干名队员，任意两名队员之间进行一场友谊赛，共进行了 36 场比赛.如果全队有 x 名队员，根据题意下列方程正确的是（ ） A． ( 1) 36x x   B． ( 1) 36x x   C． ( 1) 36 2 x x   D． ( 1) 36 2 x x  