2013年云南昆明中考数学试卷及答案(解析版) 11页

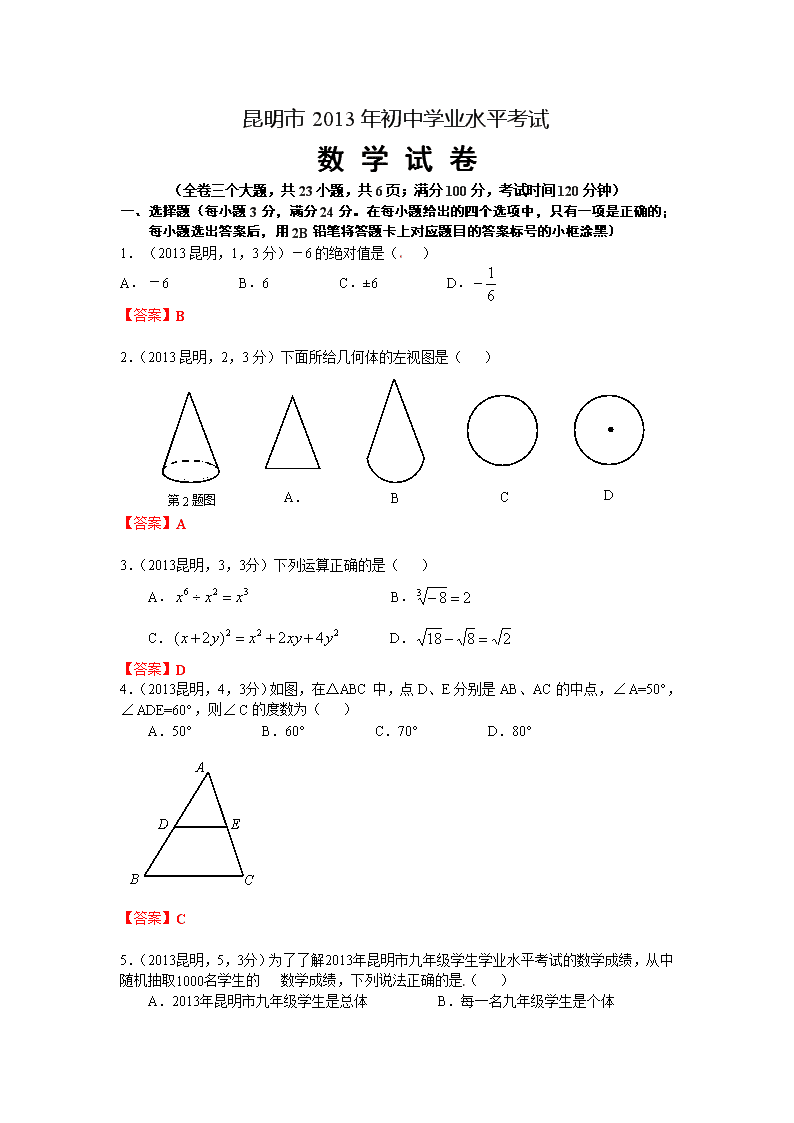
昆明市2013年初中学业水平考试 数 学 试 卷 ‎（全卷三个大题，共23小题，共6页；满分100分，考试时间120分钟）‎ 一、 选择题（每小题3分，满分24分。在每小题给出的四个选项中，只有一项是正确的； 每小题选出答案后，用2B铅笔将答题卡上对应题目的答案标号的小框涂黑）‎ 1． ‎（2013昆明，1，3分）－6的绝对值是（ ）‎ A． ‎－6 B．6 C．±6 D．‎ ‎【答案】B ‎2．（2013昆明，2，3分）下面所给几何体的左视图是（ ）‎ 第2题图 A．‎ B．‎ C．‎ D．‎ ‎【答案】A ‎3．（2013昆明，3，3分）下列运算正确的是（ ）‎ A． B．‎ C． D．‎ ‎【答案】D ‎4．（2013昆明，4，3分）如图，在△ABC中，点D、E分别是AB、AC的中点，A=50°，ADE=60°，则C的度数为（ ）‎ A．50° B．60° C．70° D．80°‎ A B C D E ‎【答案】C ‎5．（2013昆明，5，3分）为了了解2013年昆明市九年级学生学业水平考试的数学成绩，从中随机抽取1000名学生的 数学成绩，下列说法正确的是（ ）‎ A．2013年昆明市九年级学生是总体 B．每一名九年级学生是个体 C．1000名九年级学生是总体的一个样本 D．样本容量是1000‎ ‎【答案】D ‎6．（2013昆明，6，3分）一元二次方程的根的情况是（ ）‎ A．有两个不相等的实数根 B．有两个相等的实数根 C．没有实数根 D．无法确定 ‎【答案】A ‎7．（2013昆明，7，3分）如图，在边长为100米，宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，要使绿化面积为7644米²，则道路的宽应为多少米？设道路的宽为米，则可列方程为（ ）‎ A． ‎ B．‎ C． D．[来源:学科网ZXXK]‎ ‎100m ‎80m ‎【答案】C ‎8．（2013昆明，8，3分）如图，在正方形ABCD中，点P是AB上一动点（不与A、B重合），对角线AC、BD相交于点O，过点P分别作AC、BD的垂线，分别交AC、BD于点E、F，交AD、BC于点M、N。下列结论：①△APE≌△AME；②PM+PN=AC；③PE2+PF2=PO2；④△POF∽△BNF；⑤当△PMN∽△AMP时，点P是AB的中点。其中正确的结论有（ ）‎ A．5个 B．4个 C．3个 D．2个 A B C D P O M N E F ‎【答案】B 一、 填空题（每小题3分，满分18分。请考生用黑色碳素笔将答案写在答题卡相应题号后的横线上）‎ ‎9．（2013昆明，9，3分）据报道，2013年一季度昆明市共接待游客约为12340000人，将12340000人用科学记数法表示为__________人。‎ ‎【答案】1.234×107‎ ‎10．（2013昆明，10，3分）已知正比例函数的图象经过点A（－1，2），则正比例函数的解析式为__________。‎ ‎【答案】y=－2x ‎11．（2013昆明，11，3分）求9的平方根的值为__________。‎ ‎【答案】±3‎ ‎12．（2013昆明，12，3分）化简：__________。‎ ‎【答案】x+2‎ ‎13．（2013昆明，13，3分）如图，从直径为4cm的圆形纸片中，剪出一个圆心角为90°的扇形OAB，且点、A、B在圆周上，把它围成一个圆锥，则圆锥的底面圆的半径是__________cm。‎ A B O ‎【答案】‎ ‎14．（2013昆明，14，3分）在平面直角坐标系中，已知点A（2,3），在坐标轴上找一点P，使得△AOP是等腰三角形，则这样的点P共有__________个。‎ ‎【答案】8‎ 一、 解答题（共9题，满分58分。请考生用黑色碳素笔在答题卡上相应的题号后答题区域内作答，必须写出运算步骤、推理过程或文字说明，超出答题区域的作答无效。特别注意： 作图时，必须使用黑色碳素笔在答题卡上作图）‎ ‎15．（2013昆明，15，5分）（本小题5分）计算：‎ ‎【答案】解：原式=1+（－1）+3－1 =2‎ ‎16．（2013昆明，16，5分）（本小题5分）已知：如图，AD、BC相交于点，∥CD。求证：AB=CD。‎ A B C D O ‎【答案】证明：∵ AB∥CD ‎∴∠A=∠D，∠B=∠C，‎ 在△AOB和△DOC中，‎ ‎ ‎ ‎∴△AOB≌△DOC（AAS）‎ ‎∴AB=CD ‎17．（2013昆明，17，5分）（本小题5分）在平面直角坐标系中，四边形ABCD的位置如图所示，解答下列问题：‎ ‎（1）将四边形ABCD先向左平移4个单位，再向下平移6个单位，得到四边形A1B1C1D1，画出平移后的四边形A1B1C1D1；‎ ‎（1）将四边形A1B1C1D1绕点A1逆时针旋转90°，得到四边形A1B2C2D2，画出旋转后的四边形A1B2C2D2，并写出点C2的坐标。‎ O y x ‎－1‎ ‎－1‎ ‎1‎ ‎1‎ A B C D ‎ ‎ ‎[来源:学科网]‎ ‎【答案】解：（1）如图四边形A1B1C1D1即为所求；‎ ‎ （2）如图四边形A1B2C2D2即为所求，C2(1，－2)‎ O y x ‎－1‎ ‎－1‎ ‎1‎ ‎1‎ A B C D A1‎ B1‎ C1‎ D1‎ D2‎ C2‎ B2‎ ‎18．（2013昆明，18，5分）（本小题5分）‎2013年6月6日第一届南亚博览会在昆明举行。某校对七年级学生开展了“南博会知多少？”的调查活动，采取随机抽样的方法进行问卷调查，问卷调查的结果划分为“不太了解”、“基本了解”、“比较了解”、“非常了解”四个等级，对调查结果进行统计后，绘制了如下不完整的条形统计图：‎ 根据以上统计图提供的信息，回答下列问题：‎ （1） 若“基本了解”的人数占抽样调查人数的25%，此次调查抽取了_____名学生；‎ （2） 补全条形统计图；‎ （3） 若该校七年级有600名学生，请估计“比较了解”和“非常了解”的学生共有多少人？‎ ‎【答案】解：（1）40‎ ‎ （2）补全条形统计图，如下图：‎ ‎15‎ ‎ （3）“比较了解”和“非常了解”的学生共有600×（+）=390（人）‎ ‎ 答：“比较了解”和“非常了解”的学生共有390人。‎ ‎19．（2013昆明，19，6分）（本小题6分）有三张正面分别标有数字：－1，1，2的卡片，它们除数字不同外其余全部相同，现将它们背面朝上，洗匀后从中随机抽出一张记下数字，放回洗匀后再从中随机抽出一张记下数字。‎ （1） 请用列表或画树形图的方法（只选其中一种），表示两次抽出卡片上的数字的所有结果；‎ （2） 将第一次抽出的数字作为点的横坐标，第二次抽出的数字作为点的纵坐标，求点 （，）落在双曲线上的概率。‎ ‎【答案】解：（1）列表如下：‎ ‎ 第 二 次 第 一 次 ‎－1‎ ‎1‎ ‎2‎ ‎－1‎ ‎（－1，－1）‎ ‎（－1，1）‎ ‎（－1，2）‎ ‎1‎ ‎（1，－1）‎ ‎（1，1）‎ ‎（1，2）‎ ‎2‎ ‎（2，－1）‎ ‎（2，1）‎ ‎（2，2）‎ ‎－1‎ ‎1‎ ‎2‎ 开始 ‎－1‎ ‎1‎ ‎2‎ ‎－1‎ ‎1‎ ‎2‎ ‎1‎ ‎－1‎ ‎2‎ ‎（－1，－1）‎ ‎（－1，1）‎ ‎（－1，2）‎ ‎（1，－1）‎ ‎（1，1）‎ ‎（1，2）‎ ‎（2，－1）‎ ‎（2，1）‎ ‎（2，2）‎ 树形图如下： ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎(2)可能出现的点的坐标共9个，它们出现的可能性相同。‎ ‎ 落在双曲线y=上的点共有2个：（1，2），（2，1）‎ ‎ ∴P（点落在双曲线上）=。‎ ‎20．（2013昆明，20，7分）（本小题7分）如图，为了缓解交通拥堵，方便行人，在某街道计划修建一座横断面为梯形ABCD的过街天桥，若天桥斜坡AB的坡角为35°，斜坡CD的坡度为（垂直高度CE与水平宽度DE的比），上底BC=10cm，天桥高度CE=5m，求天桥下底AD的长度？（结果精确到0.1m，参考数据，，）‎ ‎【答案】解：过B点作BF⊥AD于点F ‎ ∵四边形BFEC是矩形 ‎∴BF=CE=5m,EF=BC=10m 在Rt△ABF中,∠BAF=35°‎ tan∠BAF= ‎ AF=≈≈7.14(m)‎ ‎∵斜坡CD的坡度为i=1：1.2‎ ‎∴，ED=1.2CE=1.2×5=6(m)‎ ‎∴AD=AF+FE+ED=7.17+10+6=23.14≈23.1(m)‎ 答：天桥下底AD的长度约为23.1米。‎ ‎21．（2013昆明，21，8分）（本小题8分）某校七年级准备购买一批笔记本奖励优秀学生，在购买时发现，每本笔 记本可以打九折，用360元钱购买的笔记本，打折后购买的数量比打折前多10本。‎ （1） 求打折前每本笔记本的售价是多少元？‎ （2） 由于考虑学生的需求不同，学校决定购买笔记本和笔袋共90件，笔袋每个原售价为6 元，两种物品都打九折，若购买总金额不低于360元，且不超过365元，问有哪几种 购买方案？‎ ‎【答案】解: (1)设打折前每本笔记本的售价是x元.‎ ‎ 根据题意得：‎ ‎ 解方程得：x=4‎ ‎ 经检验，x=4是原方程的解。‎ ‎(2)设购买笔记本m本，则购买笔袋(90－m)个。‎ 根据题意，得 解得：67≤m≤70,‎ ‎∵m是正整数,‎ ‎∴m=68，69，70。‎ 答:有三种购买方案：‎ 方案一：购买笔记本68本,购买笔袋22个；‎ 方案二：购买笔记本69本,购买笔袋21个；‎ 方案三：购买笔记本70本,购买笔袋20个。‎ ‎22．（2013昆明，22，8分）（本小题8分）已知：如图，AC是⊙的直径，BC是⊙的弦，点P是⊙外一点，。‎ ‎（1）求证：PB是⊙O的切线；‎ ‎（2）若OP∥BC，且OP=8，BC=2，求⊙O的半径。‎ A B C P O ‎ ‎ ‎【答案】(1)证明：连接OB，‎ ‎ ∵OB=OC，‎ ‎∴∠C=∠OBC，‎ 又∵∠PBA=∠C，‎ ‎∴∠PBA=∠OBC，‎ ‎∵AC是⊙O的直径，∴∠ABC=90°‎ 点B在圆上，OB是半径，OB⊥PB ‎∴PB是⊙O的切线。‎ ‎（2）设⊙O的半径为r ‎ ∵OC=OB，∴∠C=∠OBC ‎∵OP∥BC，∴∠POB=∠OBC ‎∴∠C=∠POB 在△ABC和△PBO中 ‎∠C=∠POB，∠ABC=∠PBO=90°‎ ‎∴△ABC∽△PBO ‎∴‎ ‎∵OP=8，BC=2，‎ ‎∴，解得：r=±（r是半径，－舍去）‎ ‎∴⊙O的半径为。‎ ‎23．（2013昆明，23，9分）（本小题9分）如图，矩形OABC在平面直角坐标系中，点A在轴的正半轴上，点C在轴的正半轴上，=4，‎ ‎=3，若抛物线的顶点在边BC上，且抛物线经过、两点，直线AC交抛物线于点D。‎ （1） 求抛物线的解析式；‎ （2） 求点D的坐标；‎ （3） 若点M在抛物线上，点N在轴上，是否存在以、、、为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由。‎O x y A B C D ‎【答案】解：（1）由题意知：A(4，0)，C(0，3)，BC=4。‎ ‎∴BC的中点坐标为（2，3）‎ 由对称性可知：抛物线的顶点坐标为（2，3）‎ 设抛物线的解析式为y=a（x－h）2+k，‎ 由抛物线的顶点坐标为（2，3），则h=2，k=3‎ 将O（0，0）代入得：0=a（0－2）2+3，解得：a=－ 抛物线的解析式为y=－x2+3x ‎(2)解：设直线AC的解析式为y=kx+b，将A(4,0),C(0，3)代入解析式可得：‎ ‎ 解得：‎ ‎ ∴直线AC的解析式为 由 解得或 ‎∴抛物线与直线AC的交点的坐标为（1，）和（4，0）‎ ‎∴点D的坐标为（1，）‎ ‎（3）存在。‎ ‎①若点M在x轴的上方 如图（1），过点D作DM∥x轴交抛物线于点M O x y A B C D M N1‎ N2‎ 图1‎ ‎∵DM=2，要使以A、D、M、N为顶点的四边形是平行四边形，须有AN=2，‎ ‎∴N1(2，0)，N2(6，0)‎ ‎②若点M在x轴的下方 图2‎ O x y A B C D M4‎ N4‎ N3‎ M3‎ 如图（2）所示，要使以A、D、M、N为顶点的四边形是平行四边形，‎ 须有|Dy|=|My|=，且MN∥AD ‎∴My=－ ‎∵点M在抛物线y=－x2+3x上 ‎∴－x2+3x=－ 解得：x1=2+，x2=2－，‎ 此时M3(2+，－)，M4(2－，－)‎ Ⅰ.当M3(2+，－)，∵M3N3∥AD 设直线M3N3 的解析式为y=－x+b,把M3(2+，－)代入解得：b=‎ 直线M3N3 的解析式为y=－x+‎ 令y=0,解得:x=－1，∴N3(－1，0)‎ Ⅱ.当M4(2－，－), ∵M4N4∥AD ‎ 同理可得直线M4N4的解析式为y=－x+ ‎ 令y=0，解得：x=－1，∴N4(－1,0) ‎ ‎ 综上所述,满足条件的点N有四个：N1(2，0)，N2(6，0)，N3(－1，0)，N4(－1，0)‎