2020九年级数学下册 第二十八章 锐角三角函数 8页

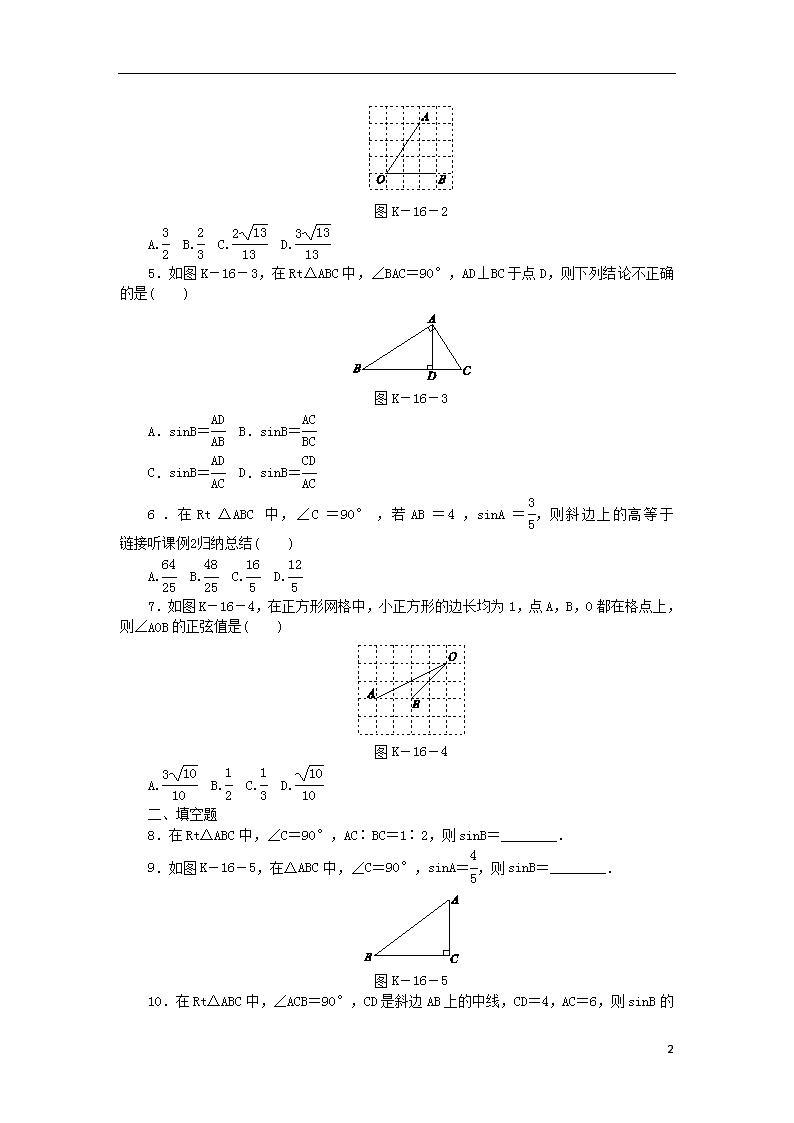
课时作业(十六)‎ ‎[28.1　第1课时　正弦]　　　　　　　　　 　　　　　　　 　‎ ‎ 一、选择题 ‎1．在Rt△ABC中，∠C＝90°，若将各边长度都扩大为原来的5倍，则∠A的正弦值(　　)‎ A．扩大为原来的5倍 B．缩小为原来的 C．扩大为原来的10倍 D．不变 ‎2．2017·日照在Rt△ABC中，∠C＝90°，AB＝13，AC＝5，则sinA的值为(　　)‎ A. B. C. D. ‎3．2017·怀化如图K－16－1，在平面直角坐标系中，点A的坐标为(3，4)，那么sinα的值是(　　)‎ 图K－16－1‎ A. B. C. D. ‎4．如图K－16－2，将∠AOB放置在5×5的正方形网格中，则sin∠AOB的值是(　　)‎ 8‎ 图K－16－2‎ A. B. C. D. ‎5．如图K－16－3，在Rt△ABC中，∠BAC＝90°，AD⊥BC于点D，则下列结论不正确的是(　　)‎ 图K－16－3‎ A．sinB＝ B．sinB＝ C．sinB＝ D．sinB＝ ‎6．在Rt△ABC中，∠C＝90°，若AB＝4，sinA＝，则斜边上的高等于(　　)‎ A. B. C. D. ‎7．如图K－16－4，在正方形网格中，小正方形的边长均为1，点A，B，O都在格点上，则∠AOB的正弦值是(　　)‎ 图K－16－4‎ A. B. C. D. 二、填空题 ‎8．在Rt△ABC中，∠C＝90°，AC∶BC＝1∶2，则sinB＝________．‎ ‎9．如图K－16－5，在△ABC中，∠C＝90°，sinA＝，则sinB＝________．‎ 图K－16－5‎ ‎10．在Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线，CD＝4，AC＝6，则sinB 8‎ 的值是________．‎ ‎11．如图K－16－6，在⊙O中，过直径AB延长线上的点C作⊙O的一条切线，切点为D，若AC＝7，AB＝4，则sinC的值为________．‎ 图K－16－6‎ ‎12．如图K－16－7，⊙O是△ABC的外接圆，AD是⊙O的直径，若⊙O的半径为，AC＝2，则sinB的值是________．‎ 图K－16－7‎ ‎13．如图K－16－8，在▱ABCD中，连接BD，已知AD⊥BD，AB＝4，sinA＝，则▱ABCD的面积是________．‎ 图K－16－8‎ 三、解答题 ‎14．在Rt△ABC中，∠C＝90°，AC＝‎1 cm，BC＝‎2 cm，求sinA和sinB的值．‎ ‎15．在Rt△ABC中，∠C＝90°.‎ ‎(1)若sinA＝，BC＝9，求AB的长；‎ ‎(2)若sinB＝，AB＝10，求BC的长．‎ 8‎ ‎16．如图K－16－9，在Rt△ABC中，∠ACB＝90°，AB＝5，BC＝3，CD⊥AB于点D，求sin∠BCD的值．‎ 图K－16－9‎ ‎17．已知：如图K－16－10，在△ABC中，AB＝AC＝13，BC＝10.求∠BAC，∠ABC的正弦值．‎ 图K－16－10‎ ‎18．如图K－16－11，小明将一张矩形纸片ABCD沿CE折叠，点B恰好落在AD边上的点F处，若AB∶BC＝4∶5.求sin∠DCF的值．‎ 图K－16－11‎ ‎ 规律探究如图K－16－12①②③，根据图中数据完成填空，再按要求答题：‎ 8‎ 图K－16－12‎ sin‎2A1＋sin2B1＝__________；‎ sin‎2A2＋sin2B2＝__________；‎ sin‎2A3＋sin2B3＝__________．‎ ‎(1)观察上述等式，猜想：在Rt△ABC中，∠C＝90°，都有sin‎2A＋sin2B＝__________；‎ ‎(2)如图K－16－12④，在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别是a，b，c，利用三角函数的定义和勾股定理，证明你的猜想．‎ 8‎ 详解详析 ‎[课堂达标]‎ ‎1．D　‎ ‎2．[解析] B　在Rt△ABC中，由勾股定理，得BC＝＝12.‎ ‎∴sinA＝＝.‎ 故选B.‎ ‎3．C ‎4．[解析] D　过点A作AC⊥OB于点C.‎ 在Rt△OAC中，OC＝2，AC＝3，‎ 则OA＝＝＝，‎ 故sin∠AOB＝＝＝.‎ ‎5．C ‎6．[解析] B　如图所示，过点C作CD⊥AB于点D.‎ 在Rt△ABC中，AB＝4，sinA＝＝，‎ ‎∴BC＝AB·sinA＝.‎ 根据勾股定理，得AC＝＝.‎ ‎∵S△ABC＝AC·BC＝AB·CD，‎ ‎∴CD＝＝.‎ ‎7．[解析] D　过点A作AC⊥OB交OB的延长线于点C，‎ 则AC＝，AO＝＝＝2 ，‎ 则sin∠AOB＝＝＝.‎ ‎8．[答案] ‎[解析] 设AC＝k(k＞0)，则BC＝2k，由勾股定理，得AB＝＝k，再由正弦的定义，得sinB＝.‎ ‎9.　10. ‎11．[答案] ‎[解析] ∵在Rt△ABC中，CD是斜边AB上的中线，CD＝4，‎ ‎∴AB＝2CD＝8，‎ 则sinB＝＝＝.‎ ‎12．[答案] ‎[解析] 如图，连接CD.‎ 8‎ ‎∵AD是⊙O的直径，‎ ‎∴∠ACD＝90°.‎ ‎∵⊙O的半径为，‎ ‎∴AD＝3，‎ ‎∴在Rt△ACD中，sinD＝＝.‎ ‎∵∠B＝∠D，‎ ‎∴sinB＝sinD＝.‎ ‎13．[答案] 3 ‎[解析] ∵AD⊥BD，‎ ‎∴∠ADB＝90°.‎ ‎∵AB＝4，sinA＝，‎ ‎∴BD＝AB·sinA＝4×＝3，‎ ‎∴AD＝＝＝，‎ ‎∴▱ABCD的面积＝AD·BD＝3 .‎ ‎14．解：在Rt△ABC中，由勾股定理，得 AB＝＝＝(cm)，‎ ‎∴sinA＝＝＝，‎ sinB＝＝＝.‎ 即sinA＝，sinB＝.‎ ‎15．解：(1)∵sinA＝，‎ ‎∴＝，即＝，‎ ‎∴AB＝15.‎ ‎(2)∵sinB＝，∴＝，‎ 即＝，∴AC＝8，‎ ‎∴BC＝＝＝6.‎ ‎16．解：∵∠ACB＝90°，CD⊥AB，‎ ‎∴∠A＋∠B＝90°，∠BCD＋∠B＝90°，‎ ‎∴∠A＝∠BCD，‎ ‎∴sin∠BCD＝sinA＝＝.‎ 8‎ ‎17．解：如图，过点A作AD⊥BC于点D，过点B作BE⊥AC于点E.‎ ‎∵AB＝AC，BC＝10，‎ ‎∴BD＝BC＝5.‎ ‎∵AB＝13，‎ ‎∴AD＝＝＝12，‎ ‎∴sin∠ABC＝＝.‎ 又∵S△ABC＝BC·AD＝AC·BE，‎ ‎∴BE＝，‎ ‎∴sin∠BAC＝＝÷13＝.‎ 即sin∠BAC＝，sin∠ABC＝.‎ ‎18．解：∵AB∶BC＝4∶5，‎ ‎∴设AB＝4x，则BC＝5x.‎ 由题意，得FC＝BC＝5x，DC＝AB＝4x.‎ 由勾股定理，得DF＝3x.‎ 在Rt△CDF中，∠D＝90°，DF＝3x，FC＝5x，‎ ‎∴sin∠DCF＝＝.‎ ‎[素养提升]‎ 解：1　1　1‎ ‎(1)1‎ ‎(2)证明：∵sinA＝，sinB＝，a2＋b2＝c2，‎ ‎∴sin2A＋sin2B＝＋＝＝1.‎ 8‎